相关试卷
-
1、若复数满足 , 则在复平面内对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
2、已知 , , 则p是q的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分又不必要条件
-
3、已知 , 分别为随机事件A,B的对立事件, , , 则( )A、 B、 C、若A,B独立,则 D、若A,B互斥,则
-
4、已知向量 , 若 , 则( )A、2 B、3 C、 D、
-
5、下列命题为真命题的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则
-
6、已知指数函数 .(1)、求的值;(2)、若 , 求的值;(3)、若 , 求的取值范围.
-
7、在等腰梯形中,.M为的中点,则( )A、 B、 C、 D、
-
8、已知空间向量、、都是单位向量,且两两垂直,则下列结论正确的是( )A、向量的模是 B、可以构成空间的一个基底 C、向量和夹角的余弦值为 D、向量与共线
-
9、已知命题 , , 若命题是假命题,则实数的取值范围为( )A、 B、 C、 D、
-
10、已知椭圆 , 抛物线的焦点均在轴上,的中心和的顶点均为原点 , 从 , 上分别取两个点,将其坐标记录于下表中:
3
-2
4
0
-4
(1)求的标准方程;
(2)若直线与椭圆交于不同的两点 , 且线段的垂直平分线过定点 , 求实数的取值范围.
-
11、定义 , 设函数 , , 记函数 , 且函数在区间的值域为 , 则的最大值为( )A、1 B、 C、 D、2
-
12、在平面直角坐标系中,已知直线与椭圆交于点A,B(A在x轴上方),且 . 设点A在x轴上的射影为N,三角形ABN的面积为2(如图1).
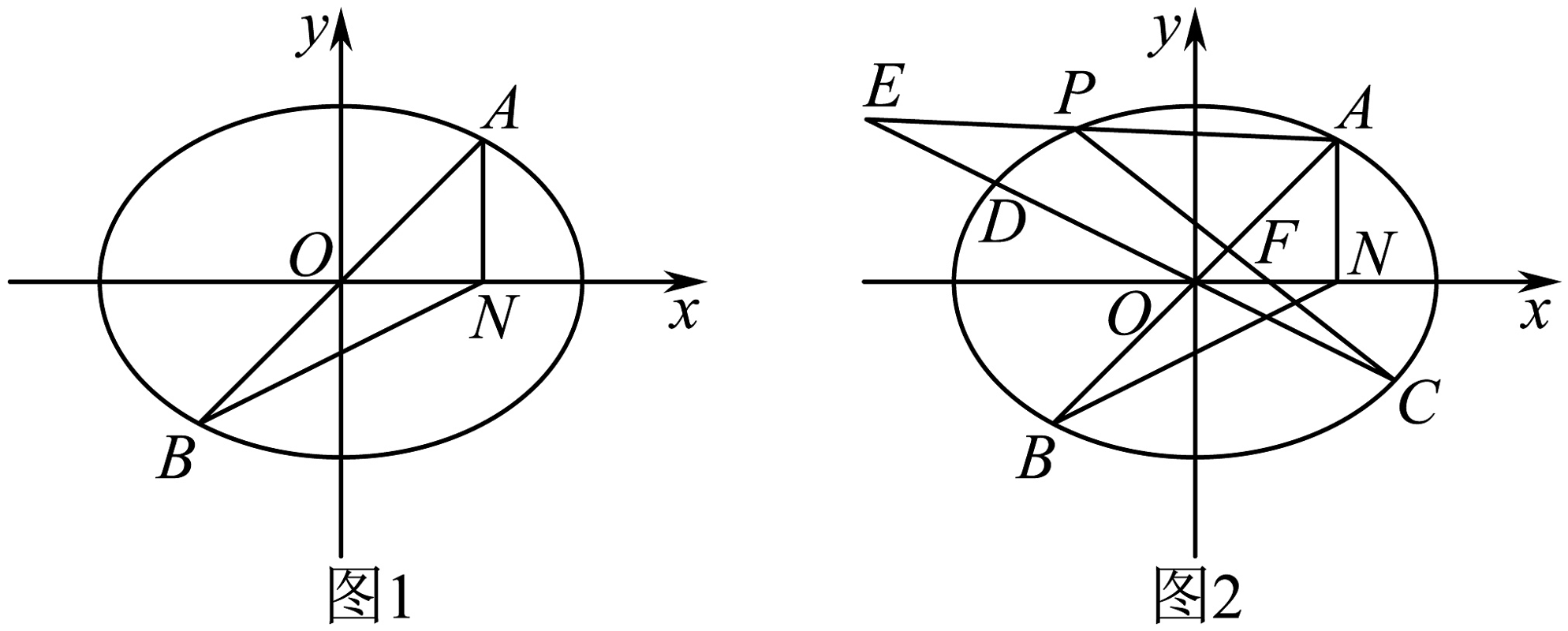
(1)求椭圆的方程;
(2)设平行于AB的直线与椭圆相交,其弦的中点为Q.
①求证:直线OQ的斜率为定值;
②设直线OQ与椭圆相交于两点C,D(D在x轴的上方),点P为椭圆上异于A,B,C,D一点,直线PA交CD于点E,PC交AB于点F,如图2,求证:为定值.
-
13、如图,在四棱锥中, , 四边形是菱形,是棱上的动点,且 .
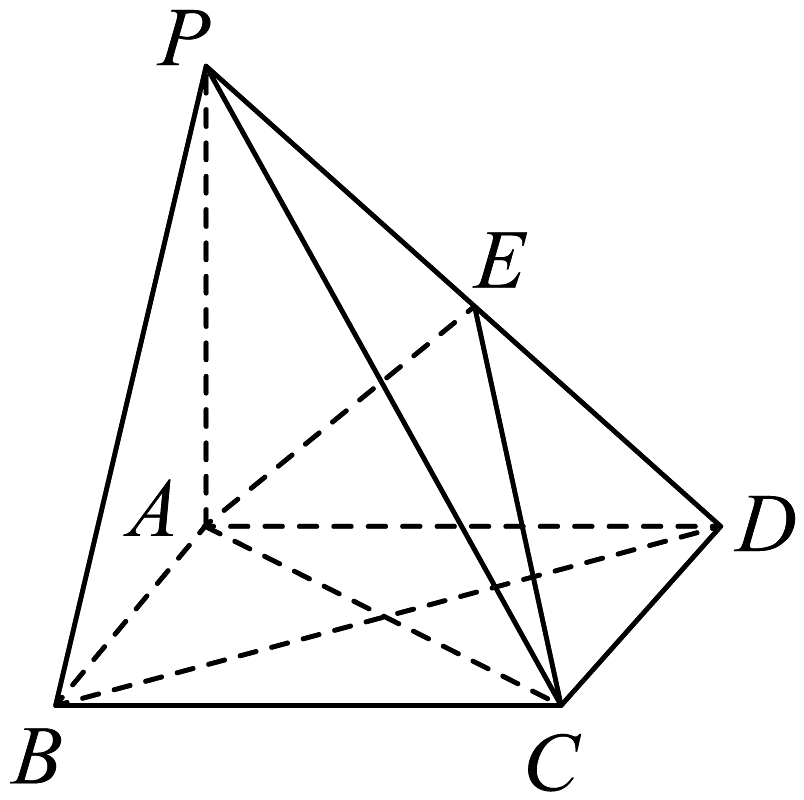 (1)、证明:平面 .(2)、是否存在实数 , 使得平面与平面所成锐二面角的余弦值是?若存在,求出的值;若不存在,请说明理由.
(1)、证明:平面 .(2)、是否存在实数 , 使得平面与平面所成锐二面角的余弦值是?若存在,求出的值;若不存在,请说明理由. -
14、会员足够多的某知名咖啡店,男会员占60%,女会员占40%.现对会员进行服务质量满意度调查.根据调查结果得知,男会员对服务质量满意的概率为 , 女会员对服务质量满意的概率为 .(1)、随机选取一名会员,求其对服务质量满意的概率;(2)、从会员中随机抽取3人,记抽取的3人中,对服务质量满意的人数为 , 求的分布列和数学期望.
-
15、若数列满足( , 为常数),则称数列为“调和数列”.已知数列为“调和数列”,下列说法正确的是( )A、若 , 则 B、若 , 且 , , 则 C、若中各项均为正数,则 D、若 , , 则
-
16、记表示 , 二者中较大的一个,函数 , , 若 , , 使得成立,则的取值范围是( )A、 B、 C、 D、
-
17、已知函数为偶函数,则不等式的解集为( )A、 B、 C、 D、
-
18、已知球的半径为1,其内接圆锥的高为 , 则该圆锥的侧面积为( )A、 B、 C、 D、
-
19、已知 , 则( )A、 B、 C、 D、
-
20、已知为虚数单位,若复数z满足 , 则( )A、1 B、 C、2 D、