相关试卷
-
1、函数的部分图象大致为( )A、
 B、
B、 C、
C、 D、
D、
-
2、下列函数为奇函数的是( )A、 B、 C、 D、
-
3、下列命题中,真命题的选项是( )A、 , B、 , C、 , D、 ,
-
4、已知样本数据为 , , , , 平均数为 , 则数据 , , , , 与原数据相比,下列数字特征一定不变的是( )A、平均数 B、方差 C、众数 D、中位数
-
5、已知集合 , 则( )A、 B、 C、 D、
-
6、如图,四棱锥的底面是边长为2菱形, , , 分别是 , 的中点.
 (1)、求证;平面;(2)、若 , , , 求平面与平面所成角的余弦值.
(1)、求证;平面;(2)、若 , , , 求平面与平面所成角的余弦值. -
7、已知函数.(1)、求曲线在点处的切线方程;(2)、证明:.
-
8、某市举办一年一度的风筝节,吸引大批游客前来观赏.为了解交通状况,有关部门随机抽取了200位游客,对其出行方式进行了问卷调查(每位游客只填写一种出行方式),具体情况如下:
出行方式
地铁
公交车
出租车
自驾
骑行
步行
频数
54
27
38
42
18
21
用上表样本的频率估计概率,低碳出行方式包括地铁、公交车、骑行和步行:
(1)、若从参加活动的所有游客中随机抽取3人,这3人中低碳出行的人数记为 , 求和;(2)、据另一项调查显示,80%的低碳出行的游客表示明年将继续参加活动,60%的非低碳出行的游客表示明年将继续参加活动,求今年参加活动的游客明年继续参加活动的概率. -
9、已知点为椭圆的右焦点,直线与椭圆相交于 , 两点,且与圆在轴右侧相切.若经过点且垂直于轴,则;若没有经过点 , 则的周长为.
-
10、若函数的图象与直线有两个交点,则的最小值为.
-
11、在中, , , , 则.
-
12、已知函数 , 则( )A、当时,在上的最大值为 B、在上单调递增 C、当时, D、当且仅当时,曲线与轴有三个交点
-
13、已知等差数列的前项和为 , 且 , 则( )A、 B、 C、当时,取得最小值 D、记 , 则数列的前项和为
-
14、已知复数满足 , 则( )A、可以是 B、若为纯虚数,则的虚部是2 C、 D、
-
15、已知函数( , ), , , 且在区间上单调,则的最大值为( ).A、 B、 C、 D、
-
16、设全集 , , 则( )A、 B、 C、 D、
-
17、已知在中,内角 , , 所对的边分别为 , , , .(1)、求角;(2)、已知直线为的平分线,且与交于点 , 若 , , 求的周长.
-
18、椭圆 , 动直线与椭圆相切于点 , 且点在第一象限.(1)、若直线的斜率为 . 求点的坐标;(2)、若过原点的直线与垂直,垂足为 , 求面积的最大值.
-
19、已知四棱锥的底面为等腰梯形, ,
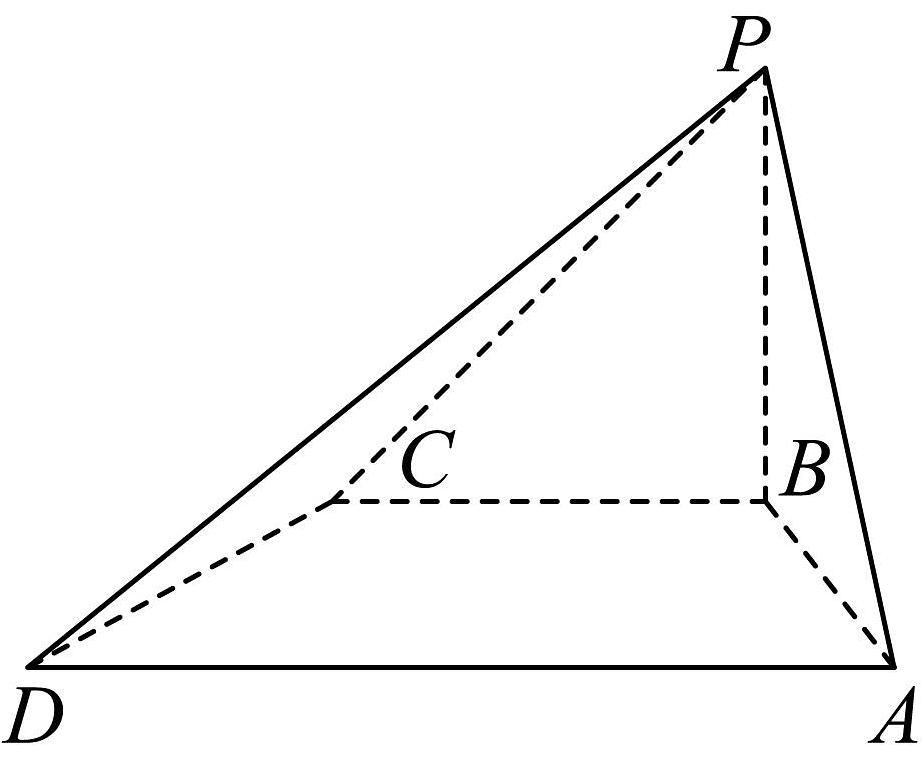 (1)、求证:平面;(2)、若四棱锥的体积为 , 求二面角的平面角的余弦值
(1)、求证:平面;(2)、若四棱锥的体积为 , 求二面角的平面角的余弦值 -
20、在平面四边形中, , 点在上且满足 , 且(1)、求;(2)、若 , 求四边形周长的最大值