相关试卷
-
1、已知三角形的三个顶点是.(1)、求边AC所在直线的斜截式方程;(2)、求边AC上的高所在直线的斜截式方程.
-
2、设有一组圆 , 存在定直线始终与圆相切.
-
3、布达佩斯的伊帕姆维泽蒂博物馆收藏的达芬奇方砖在正六边形上画了具有视觉效果的正方体图案,如图1,把三片这样的达芬奇方砖拼成图2的组合,这个组合再转换成图3所示的几何体.若图3中每个正方体的棱长为 , 则( )
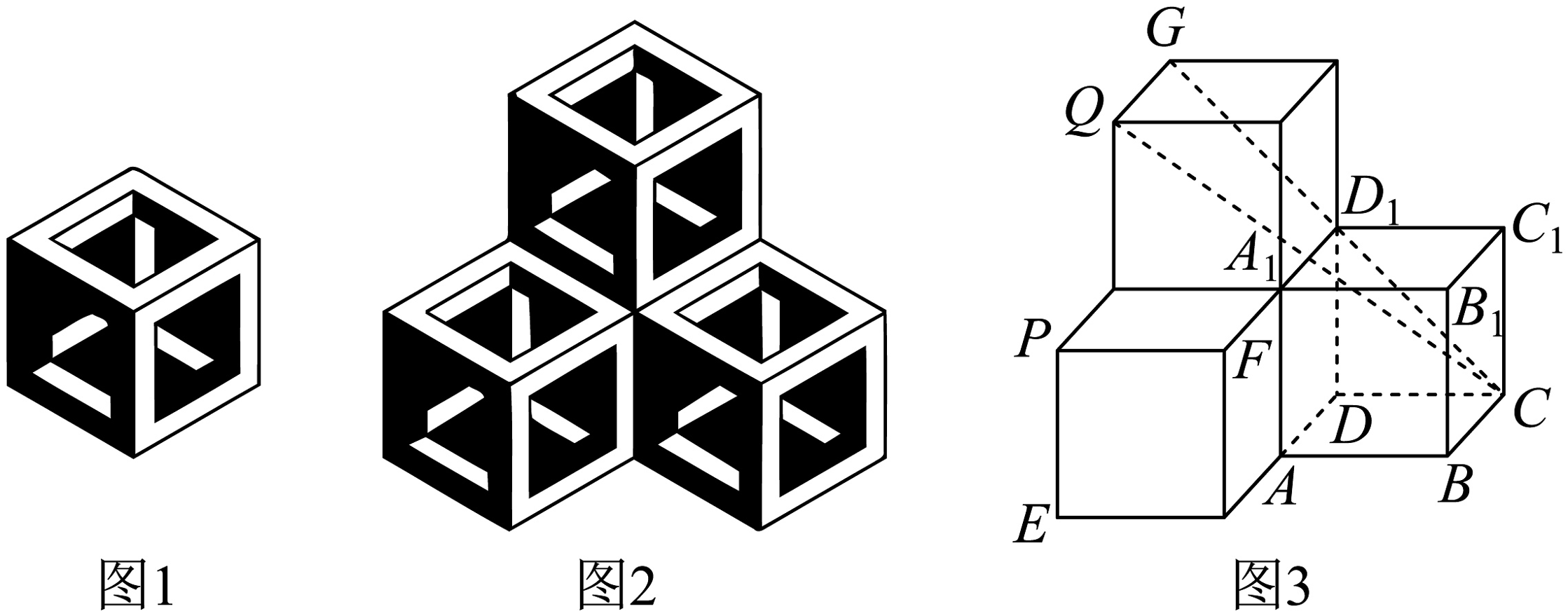 A、点到直线的距离是 B、异面直线与所成角的余弦值为 C、直线到平面的距离是 D、直线与平面所成角的正弦值为
A、点到直线的距离是 B、异面直线与所成角的余弦值为 C、直线到平面的距离是 D、直线与平面所成角的正弦值为 -
4、已知 , 椭圆: , :的离心率分别为 , .若 , 则的值可能为( )A、 B、 C、 D、
-
5、已知直线与平行,则的值可能是( )A、1 B、3 C、4 D、6
-
6、已知M,N是椭圆上关于原点对称的两点,是椭圆的右焦点,则的取值范围为( )A、[51,76] B、[52,76] C、[64,80] D、[68,80]
-
7、若直线经过两直线和的交点,则( )A、2 B、4 C、6 D、8
-
8、已知平面的一个法向量是平面内一点,是平面外一点,则点到平面的距离是( )A、 B、 C、3 D、
-
9、直线的一个方向向量是( )A、 B、 C、 D、
-
10、圆和圆的位置关系是( )A、外离 B、外切 C、内切 D、内含
-
11、圆x2+y2+2x-1=0的圆心到直线y=x+3的距离为( )A、1 B、2 C、 D、2
-
12、在平行六面体中,运算的结果为( )A、 B、 C、 D、
-
13、已知函数 , 则不等式的解集为.
-
14、甲乙两人进行一场抽卡游戏,规则如下:有编号的卡片各1张,两人轮流从中不放回的随机抽取1张卡片,直到其中1人抽到的卡片编号之和等于12或者所有卡片被抽完时,游戏结束.若甲先抽卡,求甲抽了3张卡片时,恰好游戏结束的概率是.
-
15、已知向量 , 在方向上的投影向量为 , 则( )A、 B、 C、6 D、12
-
16、已知直线和直线平行,则实数的值为( )A、 B、 C、 D、或
-
17、已知函数 , , 其中.(1)、当时,写出在上的单调性以及最大值(不用证明);(2)、若 , 函数 , , 是否存在实数 , 使得的最大值为1?若存在,求出的值,若不存在,说明理由;(3)、设 , 若对 , , 使得成立,求实数的取值范围.
-
18、已知函数( , 且)为奇函数.(1)、求实数的值;(2)、当时,判断在的单调性并用定义加以证明;(3)、记 , 解关于的不等式.
-
19、经市场调查,某商品在过去30天的日销售量(件)与日销售价格(元/件)都是时间t(天)的函数,其中(). , 每件商品的综合成本为10元.(1)、写出该店日销售利润W与时间t之间的函数关系;(2)、求该店日销售利润W的最大值.(注:销售利润=销售收入-销售成本)
-
20、已知 , ,(1)、当时,求集合A;(2)、若 , 求a的取值范围.