相关试卷
-
1、如图,直三棱柱的底面为直角三角形, , , , P是上一动点,则的最小值为( )
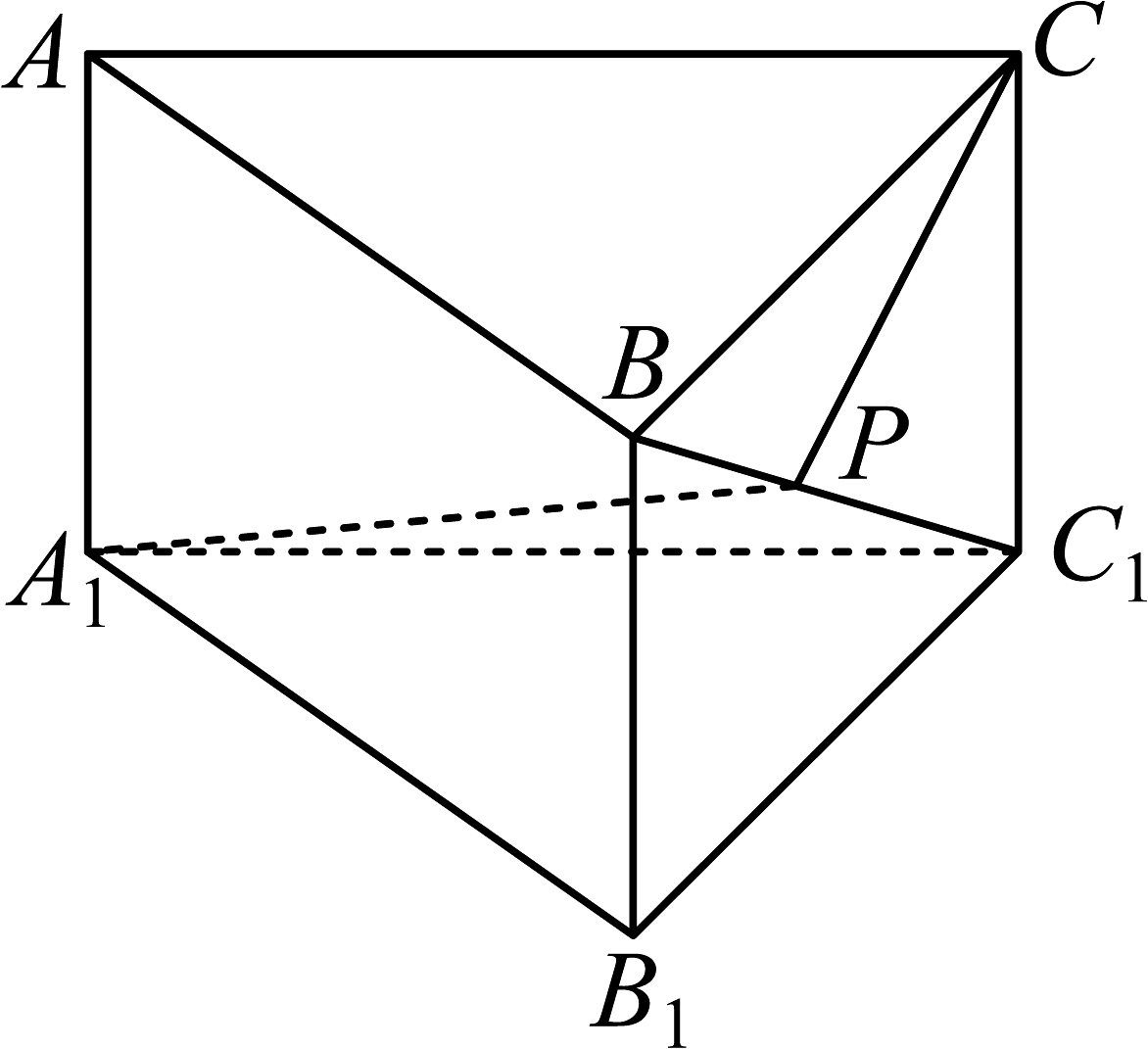 A、 B、 C、 D、
A、 B、 C、 D、 -
2、为捍卫国家南海主权,我国海军在南海海域进行例行巡逻,某天,一艘巡逻舰从海岛A出发,沿南偏东75°的方向航行到达海岛B,然后再从海岛B出发,沿北偏东45°的方向航行了海里到达海岛C.若巡逻舰从海岛A以北偏东60°的航向出发沿直线到达海岛C,则航行路程AC(单位:海里)为( )A、 B、 C、 D、
-
3、已知 , 若与的夹角为 , 则在上的投影向量为( )A、 B、 C、 D、
-
4、如图,在正四面体中,是的中点,P是线段上的动点,则直线和所成角的大小( )
 A、一定为 B、一定为 C、一定为 D、与P的位置有关
A、一定为 B、一定为 C、一定为 D、与P的位置有关 -
5、已知向量 , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
6、如图,已知等腰直角三角形是一个平面图形的直观图, , 斜边 , 则这个平面图形的面积是( )
 A、 B、1 C、 D、
A、 B、1 C、 D、 -
7、若函数在区间上单调递增,则的取值范围是( )A、 B、 C、 D、
-
8、为了节能减排,某农场决定安装一个可使用10年的太阳能供电设备.使用这种供电设备后,该农场每年消耗的电费C(单位:万元)与太阳能电池面积x(单位:平方米)之间的函数关系为 , (m为常数),已知太阳能电池面积为5平方米时,每年消耗的电费为12万元.安装这种供电设备的工本费为(单位:1万元),记为该农场安装这种太阳能供电设备的工本费与该农场10年消耗的电费之和(1)、写出的解析式;(2)、当x为多少平方米时,取得最小值?最小值是多少万元?
-
9、已知函数.(1)、用定义进行证明函数在的单调性.(2)、已知函数 , 若对任意的 , , 使得 , 求实数m的取值范围.
-
10、文化自信,服装先行,近年来汉服文化成为了一种时尚的潮流,“汉服热”的本质是对中华民族传统文化的自觉、自知、自信.内育文化强底气,外引项目强经济,汉服体验项目的盛行也带动了文化古镇的经济发展.近30天,某文化古镇的一汉服体验店,汉服的日租赁量P(件)与日租赁价格W(元/件)都是时间t(天)的函数,其中 , .每件汉服的日综合成本为20元.(1)、写出该店日租赁利润Y与时间t之间的函数关系;(2)、求该店日租赁利润Y的最大值.(注:租赁利润=租赁收入-租赁成本)
-
11、实数 , 满足 , 则的最小值为.
-
12、函数的单调递增区间为.
-
13、已知函数 , 若 , 恒成立,则( )A、函数是奇函数 B、函数是增函数 C、 , 是真命题 D、m可以为0
-
14、下列说法中正确的有( )A、函数在上单调递增 B、函数的定义域是 , 则函数的定义域为 C、不等式的解集为 D、函数关于点中心对称
-
15、已知函数 , 若的最小值为 , 则实数a的取值范围是( )A、 B、 C、 D、
-
16、已知函数的图象关于点对称,且 , , , 则的图象可能是( )A、
 B、
B、 C、
C、 D、
D、
-
17、 , , , 则( )A、 B、 C、 D、
-
18、“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
19、已知集合 , , 若 , 则实数a的值为( )A、0 B、1 C、1或3 D、3
-
20、已知空间向量 , , 下列结论正确的是( )A、 B、 , 夹角的余弦值为 C、若直线l的方向向量为 , 平面的法向量为 , 且 , 则实数 D、在上的投影向量为