版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、已知 $\vec{a} = (2, 2, 1), \vec{b} = (1, 0, 0)$ ，则 $\vec{a}$ 在 $\vec{b}$ 上的投影向量的坐标为.

查看解析
2、对于直线 $l_{1} : a x + 2 y + 3 a = 0$ 和直线 $l_{2} : 3 x + (a - 1) y + 3 - a = 0$ ．以下说法正确的有（）

A、直线 $l_{2}$ 一定过定点 $(- \frac{2}{3}, 1)$ B、若 $l_{1} ⊥ l_{2}$ ，则 $a = \frac{2}{5}$ C、若 $l_{1} // l_{2}$ ，则 $a = 3$ D、点 $P (1, 3)$ 到直线 $l_{1}$ 的距离的最大值为 $\sqrt{5}$

查看解析
3、已知在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为2，点E，F分别是直线 $A_{1} B$ 与 $B_{1} D_{1}$ 上的点，则线段EF长度的最小值为（）

A、 $\frac{2 \sqrt{3}}{3}$ B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、2

查看解析
4、已知菱形 $A B C D$ 中， $∠ A B C = 60 °$ ，沿对角线AC折叠之后，使得平面 $B A C ⊥$ 平面 $D A C$ ，则二面角 $B - C D - A$ 的余弦值为（）

A、2 B、 $\frac{1}{2}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{5}}{5}$

查看解析
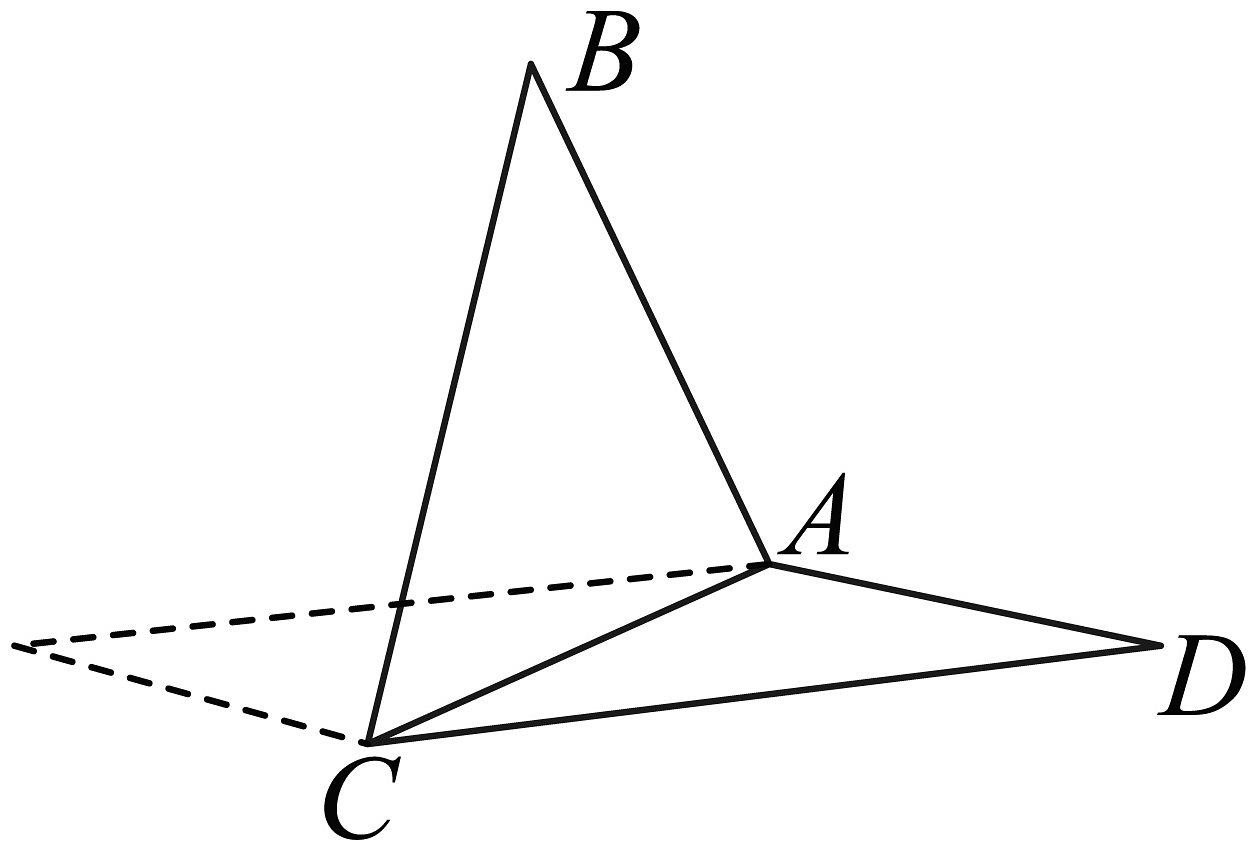5、已知平面 $α$ 内有一个点 $M (1, - 1, 2)$ ，平面 $α$ 的一个法向量是 $\vec{n} = (2, - 1, 2)$ ，则下列点 $P$ 中，在平面 $α$ 内的是（）

A、 $P (2, 3, 3)$ B、 $P (- 2, 0, 1)$ C、 $P (- 4, 4, 0)$ D、 $P (3, - 3, 4)$

查看解析
6、甲、乙两名射击运动员进行射击比赛，甲的中靶概率为0.8，乙的中靶概率为0.9，设 $A =$ “甲中靶”， $B =$ “乙中靶”，则（）

A、A与B，A与 $\bar{B}$ ， $\bar{A}$ 与B， $\bar{A}$ 与 $\bar{B}$ 都相互独立 B、 $A \bar{B}$ 与 $B \bar{A}$ 是对立事件 C、 $P (\bar{A} \bar{B}) = 0.98$ D、 $P (A B \cup \bar{A} B \cup A \bar{B}) = 0.02$

查看解析
7、如图，在斜三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $M$ 为 $B C$ 的中点， $N$ 为 $A_{1} C_{1}$ 上靠近 $A_{1}$ 的三等分点，设 $\vec{A B} = \vec{a}$ ， $\vec{A C} = \vec{b}$ ， $\vec{A A_{1}} = \vec{c}$ ，则用 $\vec{a}$ ， $\vec{b}$ ， $\vec{c}$ 表示 $\vec{N M}$ 为（）

A、 $\frac{1}{2} \vec{a} + \frac{1}{6} \vec{b} - \vec{c}$ B、 $- \frac{1}{2} \vec{a} + \frac{1}{6} \vec{b} + \vec{c}$ C、 $\frac{1}{2} \vec{a} - \frac{1}{6} \vec{b} - \vec{c}$ D、 $- \frac{1}{2} \vec{a} - \frac{1}{6} \vec{b} + \vec{c}$

查看解析
8、已知向量 $\vec{a} = (- 3, 2, 1)$ ， $\vec{b} = (2, 2, - 1)$ ， $\vec{c} = (m, 4, 0)$ ，若 $\vec{a}$ ， $\vec{b}$ ， $\vec{c}$ 共面，则 $m =$ （）

A、2 B、3 C、 $- 1$ D、 $- 5$

查看解析
9、若函数 $f (x) = \sqrt{3} \sin x + 2 \cos^{2} \frac{x}{2}$ ， $△ A B C$ 的角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ，且 $f (A) = 3$ .
（1）当 $\frac{b + c}{a}$ 取最大值时，判断 $△ A B C$ 的形状；
（2）在 $△ A B C$ 中， $D$ 为 $B C$ 边的中点，且 $A D = \sqrt{13}$ ， $A C = 2$ ，求 $B C$ 的长.

查看解析
10、如图， $P D C E$ 为矩形， $A B C D$ 为梯形，平面 $P D C E ⊥$ 平面 $A B C D$ ， $∠ B A D = ∠ A D C = 90 °$ ， $A B = A D = \frac{1}{2} C D = a$ ， $P D = \sqrt{2} a$ ．

(1)、若 $M$ 为 $P A$ 中点，求证： $A C ∥$ 平面 $M D E$ ；

(2)、求直线 $P B$ 与直线 $C D$ 所成角的大小；

(3)、设平面 $P A D \cap$ 平面 $E B C = l$ ，试判断 $l$ 与平面 $A B C D$ 能否垂直？并求平面 $P A D$ 与平面 $E B C$ 所成锐二面角的大小．

查看解析
11、已知四棱锥A—BCDE，AB=BC=AC=BE=1，CD=2BE=2，CD $⊥$ 面ABC，BE∥CD，F为AD的中点．

(1)、求证：EF∥面ABC；

(2)、求四棱锥A—BCDE的体积，

查看解析
12、在 $△ A B C$ 中，内角A，B，C所对边的长分别为a，b，c，且满足 $b \cos \frac{B + C}{2} = a \sin B$ .

(1)、求A；

(2)、若 $a = \sqrt{19}$ ， $\overset{⃑}{B A} \cdot \overset{⃑}{A C} = 3$ ， AD是 $△ A B C$ 的中线，求AD的长.

查看解析
13、已知向量 $\vec{a} = (- 3, 1), \vec{b} = (1, - 2), \vec{m} = \vec{a} + k \vec{b} (k \in R)$

(1)、向量 $\vec{a}, \vec{b}$ 夹角的余弦值；

(2)、若向量 $\vec{m}$ 与 $2 \vec{a} - \vec{b}$ 垂直，求实数k的值；

(3)、若向量 $\vec{c} = (1, - 1)$ ，且 $\vec{m}$ 与向量 $k \vec{b} + \vec{c}$ 平行，求实数k的值.

查看解析
14、如图，在 $△ A B C$ 中， $D$ 是 $B C$ 的中点，点 $E$ 在 $A B$ 上，且 $B E = 2 E A, A D$ 与 $C E$ 交于点 $O$ ，设 $\vec{A O} = λ \vec{A D}$ .

(1)、求 $λ$ 的值；

(2)、当 $A B = 5, A C = 3$ 时，求 $\vec{A O} \cdot \vec{B C}$ 的值.

查看解析
15、中国有悠久的金石文化，印信是金石文化的代表之一.如下图的印信，可以看成是将一个棱长等于2cm的正方体截去8个一样的四面体之后得到的，则该印信的所有棱长之和等于cm，该印信的表面积等于 ${cm}^{2}$ .

查看解析
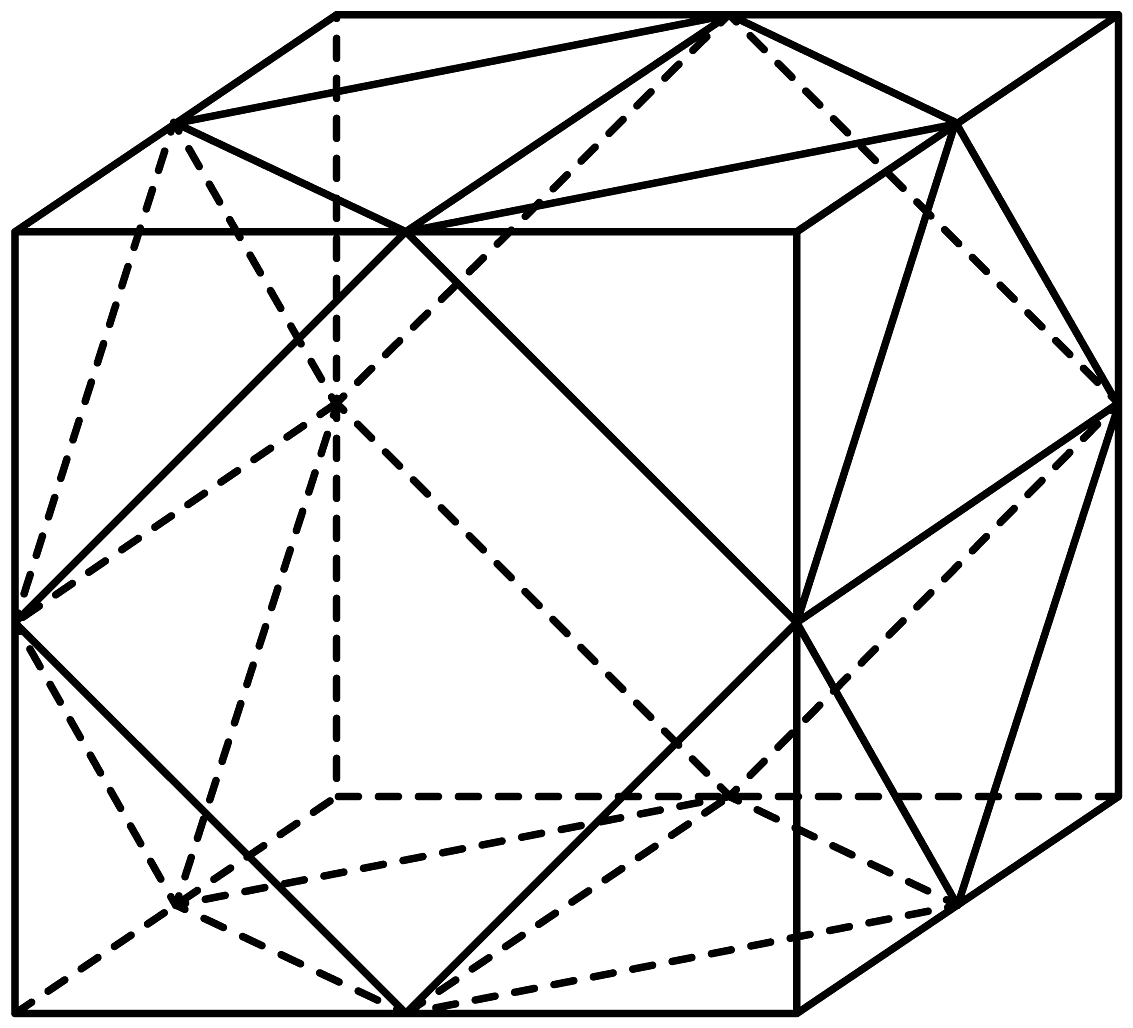
16、已知圆锥的侧面展开图是一个半径为 $2 \sqrt{3}$ 的半圆，则圆锥的底面半径为；若该圆锥的顶点及底面圆周在球O的表面上，则球O的体积为.

查看解析
17、 $- 4 + 3 i$ 是关于 $x$ 的方程 $x^{2} + p x + q = 0 (p, q \in R)$ 的根， $p =$ ．

查看解析
18、若 $\vec{A B} = (3, - 6)$ ， $B (- 2, 3)$ ，则线段AB的靠近B的三等分点P的坐标为.

查看解析
19、如图，在边长为2的正方形 $S G_{1} G_{2} G_{3}$ 中，E、F分别是 $G_{1} G_{2}$ 、 $G_{2} G_{3}$ 的中点.若沿SE、SF及EF把这个正方形折成一个四面体，使 $G_{1}$ 、 $G_{2}$ 、 $G_{3}$ 三点重合，重合后的点记为G，则（）

A、 $G S ⊥ E F$ B、点G到平面SEF的距离为 $\frac{3}{4}$ C、三棱锥 $G - S E F$ 的外接球表面积为 $6 π$ D、二面角 $E - G S - F$ 等于 $45 °$

查看解析
20、锐角△ABC中，内角A，B，C所对边分别为a，b，c，且 $c - b = 2 b \cos A$ ，下列结论正确的是（）

A、A=2B B、B的取值范围为 $(0, \frac{π}{4})$ C、 $\frac{a}{b}$ 的取值范围为 $(\sqrt{2}, \sqrt{3})$ D、 $\frac{1}{\tan B} - \frac{1}{\tan A} + 2 \sin A$ 的取值范围为 $(\frac{5 \sqrt{3}}{3}, 3)$

查看解析

上一页 865 866 867 868 869 下一页跳转