相关试卷
-
1、如图,在中, , 点是线段上一点.
 (1)、若点是线段的中点,试用和表示向量;(2)、若 , 求实数的值.
(1)、若点是线段的中点,试用和表示向量;(2)、若 , 求实数的值. -
2、已知向量与的夹角为 , 且 , .(1)、求(2)、当为何值时,向量与互相垂直.
-
3、在中, , 三角形的面积等于 , 则的长为.
-
4、若为纯虚数,则复数的虚部为.
-
5、已知向量 , 满足 , , 则 .
-
6、已知函数的部分图象如图所示,下列说法正确的是( )
 A、的图象关于点对称 B、的图象关于直线对称 C、将函数的图象向左平移个单位长度得到函数的图象 D、函数在单调递增
A、的图象关于点对称 B、的图象关于直线对称 C、将函数的图象向左平移个单位长度得到函数的图象 D、函数在单调递增 -
7、对于任意的平面向量、、 , 下列说法错误的是( )A、若且 , 则 B、若 , 且 , 则 C、若且 , 则 D、
-
8、已知复数满足 , 则下列关于复数z的结论正确的是( )A、 B、复数的共轭复数为 C、复平面内表示复数的点位于第一象限 D、复数是方程的一个根
-
9、若 , , 则=( )A、 B、 C、 D、
-
10、已知平面向量 , , 则在上的投影向量为( )A、 B、 C、 D、
-
11、在中,角的对边分别为 , 若 , , 则A、 B、 C、 D、1
-
12、为了得到函数的图象,只需把函数的图象上所有的点( )A、向左平行移动个单位长度 B、向左平行移动个单位长度 C、向右平行移动个单位长度 D、向右平行移动个单位长度
-
13、已知=4,=8,与的夹角为120°,则=( )A、 B、 C、 D、
-
14、已知 , 且与垂直,则( )A、 B、 C、1 D、2
-
15、( )A、 B、 C、 D、
-
16、下列函数中,既是偶函数又在上是递减的函数是( )A、 B、 C、 D、
-
17、已知函数是定义在上的奇函数,当时,.(1)、当时,求的解析式;(2)、判断在上的单调性,并用定义证明;(3)、若对于恒成立,求的取值范围.
-
18、在正方体中,面对角线 , 上各有一个动点 , , 使得直线平面.
 (1)、当 , 为对角线 , 的中点,为的中点时,证明:平面平面;(2)、当正方体棱长为2时,求线段长度的最小值.
(1)、当 , 为对角线 , 的中点,为的中点时,证明:平面平面;(2)、当正方体棱长为2时,求线段长度的最小值. -
19、如图,在平行四边形中,为的中点,为上一点且满足 , , .
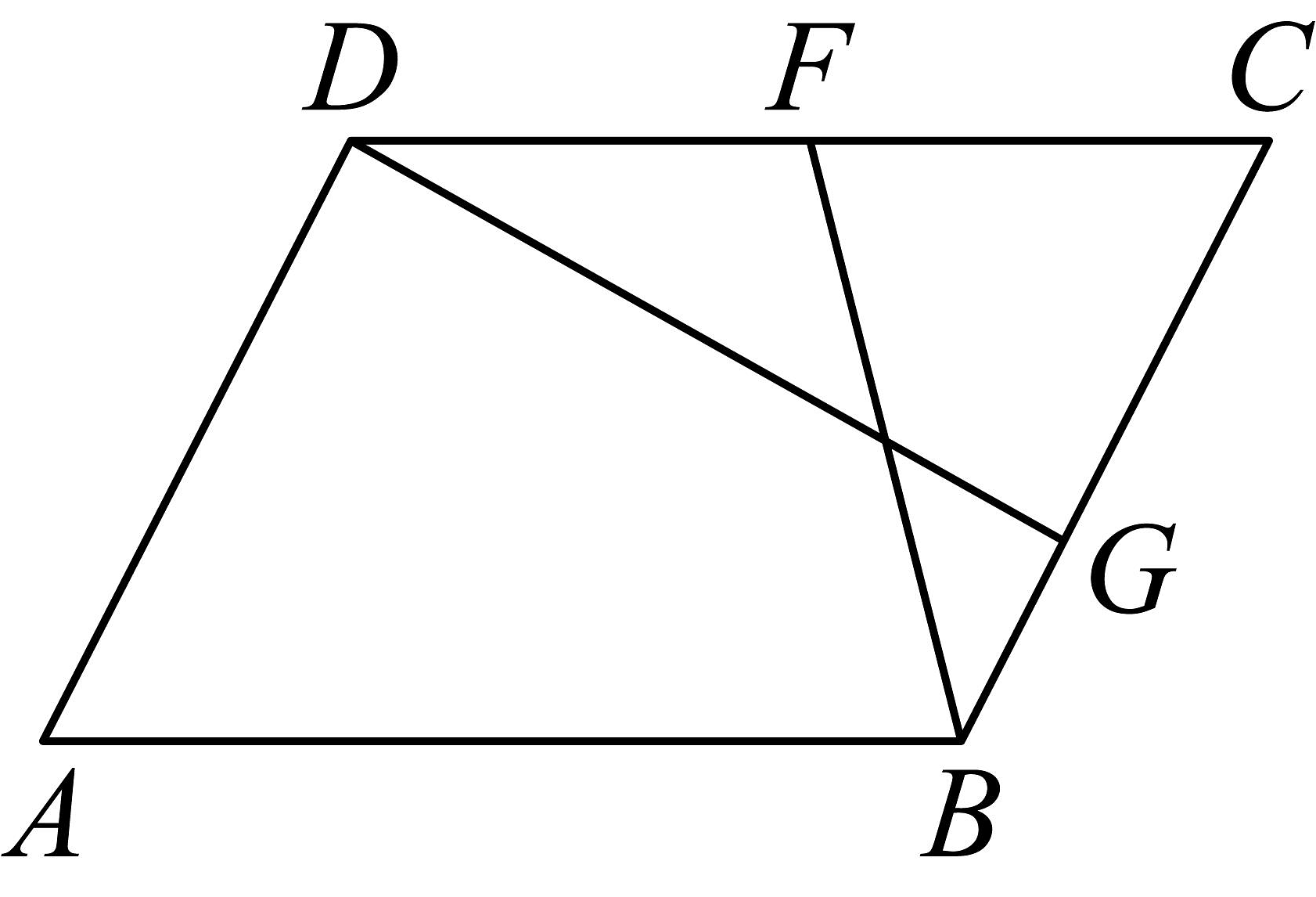 (1)、试用向量 , 表示 , ;(2)、若 , , 求向量 , 夹角的余弦值.
(1)、试用向量 , 表示 , ;(2)、若 , , 求向量 , 夹角的余弦值. -
20、如图,在正方体中,点为棱的中点.

(1)求证:平面;
(2)求异面直线与所成角的余弦值.