版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、已知复数 $z = 2 + i$ ，其中 $i$ 是虚数单位，则 $\bar{z}$ 的虚部为（）

A、2 B、 $- i$ C、1 D、 $- 1$

查看解析
2、已知圆 $A_{1} ： {(x + 1)}^{2} + y^{2} = 16$ ，直线 $l_{1}$ 过点 $A_{2} (1 ， 0)$ 且与圆 $A_{1}$ 交于点B，C，BC中点为D，过 $A_{2} C$ 中点E且平行于 $A_{1} D$ 的直线交 $A_{1} C$ 于点P，记P的轨迹为Γ

(1)、求Γ的方程；

(2)、坐标原点O关于 $A_{1}$ ， $A_{2}$ 的对称点分别为 $B_{1}$ ， $B_{2}$ ，点 $A_{1}$ ， $A_{2}$ 关于直线 $y = x$ 的对称点分别为 $C_{1}$ ， $C_{2}$ ，过 $A_{1}$ 的直线 $l_{2}$ 与Γ交于点M，N，直线 $B_{1} M$ ， $B_{2} N$ 相交于点Q.请从下列结论中，选择一个正确的结论并给予证明.
① $△ Q B_{1} C_{1}$ 的面积是定值；② $△ Q B_{1} B_{2}$ 的面积是定值：③ $△ Q C_{1} C_{2}$ 的面积是定值.

查看解析
3、某学校为提升学生的科学素养，要求所有学生在学年中完成规定的学习任务，并获得相应过程性积分.现从该校随机抽取100名学生，获得其科普测试成绩（百分制，且均为整数）及相应过程性积分数据，整理如下表：
科普测试成绩x
科普过程性积分
人数
$90 \leq x \leq 100$
4
10
$80 \leq x < 90$
3
a
$70 \leq x < 80$
2
b
$60 \leq x < 70$
1
23
$0 \leq x < 60$
0
2

(1)、当 $a = 35$ 时，
（i）从该校随机抽取一名学生，估计这名学生的科普过程性积分不少于3分的概率；
（ⅱ）从该校科普测试成绩不低于80分的学生中随机抽取2名，记X为这2名学生的科普过程性积分之和，估计X的数学期望 $E (X)$ ；

(2)、从该校科普过程性积分不高于1分的学生中随机抽取一名，其科普测试成绩记为 $Y_{1}$ ，上述100名学生科普测试成绩的平均值记为 $Y_{2}$ .若根据表中信息能推断 $Y_{1} \leq Y_{2}$ 恒成立，直接写出a的最小值.

查看解析
4、如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为菱形， $P A ⊥$ 平面 $A B C D ， A C$ 与 $B D$ 相交于点 $E$ ，点 $F$ 在 $P C$ 上， $E F ⊥ P C ， A C = 4 \sqrt{2} ， B D = 4 ， E F = 2$ ．

(1)、证明： $D F ⊥$ 平面 $P B C$ ；

(2)、若 $P A$ 与平面 $B D F$ 所成的角为 $α$ ，平面 $P A D$ 与平面 $P B C$ 的夹角为 $β$ ，求 $α + β$ ．

查看解析
5、已知直线 $l : a x + b y - 3 = 0$ 经过点 $(a, b - 2)$ ，则原点到点 $P (a, b)$ 的距离可以是．（答案不唯一，写出你认为正确的一个常数就可以）

查看解析
6、已知 $\ln \frac{a}{b} = 2$ ，则 $\ln a^{2} - \ln b^{2} =$ .

查看解析
7、勒洛四面体是一个非常神奇的“四面体”，它能在两个平行平面间自由转动，并且始终保持与两平面都接触.勒洛四面体是以正四面体的四个顶点为球心，以正四面体的棱长为半径的四个球的相交部分围成的几何体，若用棱长为4的正四面体 $A B C D$ 作勒洛四面体，如图，则下列说法正确的是（）

A、平面 $A B C$ 截勒洛四面体所得截面的面积为 $8 π - 8 \sqrt{3}$ B、记勒洛四面体上以C，D为球心的两球球面交线为弧 $A B$ ，则其长度为 $\frac{4 π}{3}$ C、该勒洛四面体表面上任意两点间距离的最大值为4 D、该勒洛四面体能够容纳的最大球的半径为 $4 - \sqrt{6}$

查看解析
8、已知点 $F (- c, 0) (c > 0)$ 是双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ 的左焦点，过 $F$ 且平行于双曲线渐近线的直线与圆 $x^{2} + y^{2} = c^{2}$ 交于点 $F$ 和另一个点 $P$ ，且点 $P$ 在抛物线 $y^{2} = 4 c x$ 上，则该双曲线的离心率是（）

A、 $\sqrt{5}$ B、 $\frac{3 + \sqrt{5}}{2}$ C、 $\sqrt{\frac{\sqrt{5} + 1}{2}}$ D、 $\frac{\sqrt{5} - 1}{2}$

查看解析
9、下图展示了一个由区间 $(0, 1)$ 到实数集R的映射过程：区间 $(0, 1)$ 中的实数 $m$ 对应数轴上的点 $M$ （如图1）；将线段 $A B$ 围成一个圆，使两端点 $A$ 、 $B$ 恰好重合（从 $A$ 到 $B$ 是逆时针，如图2）；再将这个圆放在平面直角坐标系中，使其圆心在y轴上，点 $A$ 的坐标为 $(0, 1)$ （如图3），图3中直线 $A M$ 与x轴交于点 $N (n, 0)$ ，则 $m$ 的象就是 $n$ ，记作 $f (m) = n$ ．
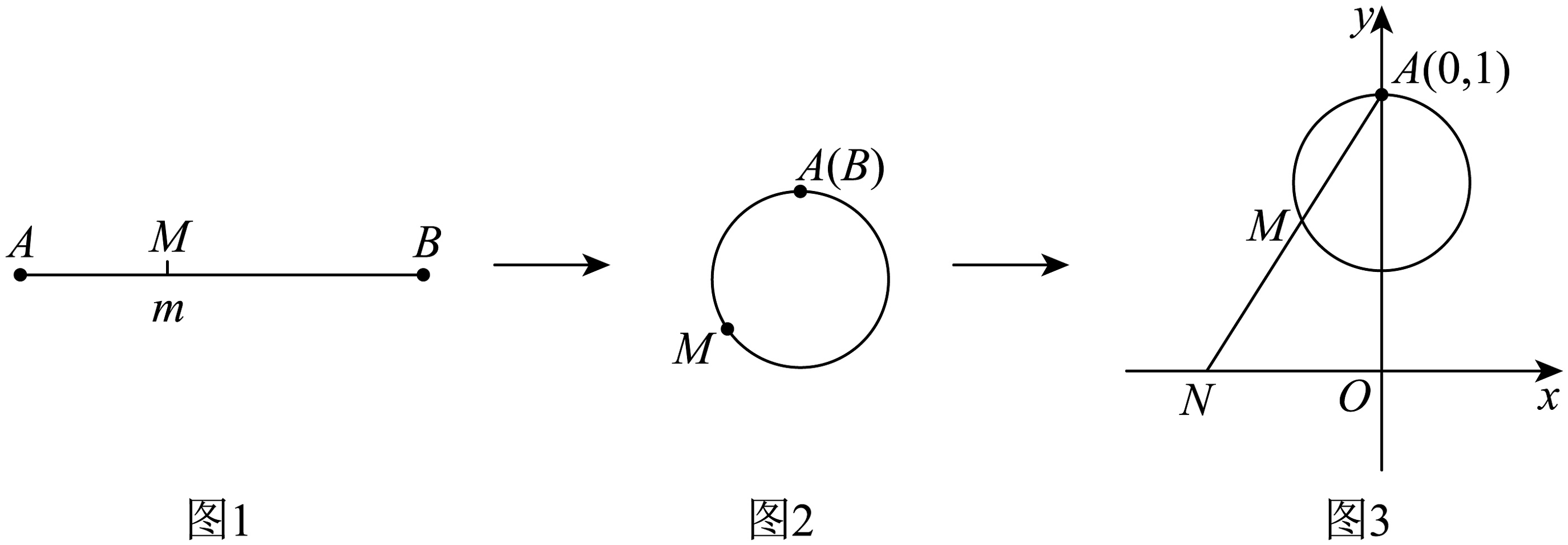
则下列命题中正确的是（）

A、 $f (\frac{1}{4}) = 1$ B、 $f (x)$ 是奇函数 C、 $f (x)$ 在其定义域上单调递增 D、 $f (x)$ 的图象关于 $y$ 轴对称

查看解析
10、二项式 ${(2 \sqrt{x} - \frac{1}{\sqrt{x}})}^{8}$ 的展开式中的常数项为（）

A、1792 B、－1792 C、1120 D、－1120

查看解析
11、 $A = \{1, a\}$ ， $B = \{2, 3, 4\}$ ，且 $A \cup B = {1,2, 3,4}$ ，则实数 $a$ 取值的集合是（）

A、 ${1,2, 3,4}$ B、 ${2,3, 4}$ C、 ${2}$ D、 ${3}$

查看解析
12、若函数 $f (x)$ 满足下列条件：在定义域内存在 $x_{0}$ ，使得 $f (x_{0} + 1) = f (x_{0}) + f (1)$ 成立，则称函数 $f (x)$ 具有性质 $M$ ：反之，若 $x_{0}$ 不存在，则称函数 $f (x)$ 不具有性质 $M$ .

(1)、判断函数 $f (x) = 2^{x}$ 是否具有性质 $M$ ，若具有性质 $M$ ，求出对应的 $x_{0}$ 的值；若不具有性质 $M$ ，说明理由.

(2)、已知函数 $h (x) = lg \frac{a}{x^{2} + 1}$ 具有性质 $M$ ，求 $a$ 的取值范围.

(3)、证明函数 $g (x) = 2^{x} + x^{2}$ 具有性质 $M$ .

查看解析
13、已知定义域为 $R$ 的函数 $f (x) = \frac{2^{x} + a}{2^{x} - a}$ 是奇函数．

(1)、求实数 $a$ 的值；

(2)、判断 $f (x)$ 的单调性，并用单调性的定义证明；

(3)、当 $x \in (0, + \infty)$ 时， $f (x^{2}) + f (- k x + 1) > 0$ 恒成立，求实数 $k$ 的取值范围．

查看解析
14、海水养殖场进行某水产品的新､旧网箱养殖方法的产量对比，收获时各随机抽取了100个网箱，测量各箱水产品的产量（单位： $kg$ ），其频率分布直方图如图所示．两种养殖方法的箱产量相互独立．

(1)、将所抽取的100个新养殖法网箱中产量低于40 $kg$ 和不低于65 $kg$ 的网箱收集到一起，再从中随机抽取2箱，恰有一箱产量不低于65 $kg$ 的概率．

(2)、用频率估计概率，从运用新､旧网箱养殖方法的水产品中各随机抽取一个网箱，估计两个网箱中至少有一箱产量不低于55 $kg$ 的概率；

(3)、求频率分布直方图中 $a$ 的值．假定新､旧网箱养殖方法网箱数不变，为了提高总产量，根据样本中两种养殖法的平均箱产量，该养殖场下一年应采用哪种养殖法更合适？（直接写出结果）

查看解析
15、在 $△ A B C$ 中，点 $D, E$ 分别在边 $B C$ 和边 $A B$ 上，且 $D C = 2 B D, B E = 2 A E, A D$ 交 $C E$ 于点 $P$ ，设 $\vec{B C} = \vec{a}, \vec{B A} = \vec{b}$ ．

(1)、用 $\vec{a}, \vec{b}$ 表示 $\vec{E C}$ 和 $\vec{D A}$ ；

(2)、若 $\vec{D P} = \frac{4}{7} \vec{D A}, \vec{E P} = t \vec{E C}$ ，用 $\vec{a}, \vec{b}$ 表示 $\vec{B P}$ ，并求实数 $t$ 的值；

(3)、在边 $A C$ 上有点 $F$ ，使得 $\vec{A C} = 5 \vec{A F}$ ，求证： $B, P, F$ 三点共线．

查看解析
16、定义域为 $R$ 的函数 $f (x)$ 同时满足以下两条性质：
①存在 $x_{0} \in R$ ，使得 $f (x_{0}) \neq 0$ ；
②对于任意 $x \in R$ ，有 $f (x + 1) = 2 f (x)$ .
根据以下条件，分别写出满足上述性质的一个函数.
（i）若 $f (x)$ 是增函数，则 $f (x) =$ ；
（ⅱ）若 $f (x)$ 不是单调函数，则 $f (x) =$ .

查看解析
17、有四张大小相同标有数字的卡片，如图所示．从这四张卡片中随机抽一张，令事件 $A_{i}$ ：“抽到卡片上有数字 $i$ ”， $i = 1, 2, 3$ ，则 $P (A_{1}) =$ ；已知命题 $p$ ：事件 $A_{2}$ 与 $A_{3}$ 相互独立，则 $p$ 为命题（用“真”“假”填空）

查看解析
18、已知甲、乙两组数据已整理成如图所示的茎叶图，则甲组数据的中位数是，乙组数据的25%分位数是．

查看解析
19、若 $p : \forall x \in (0, + \infty), x + \frac{1}{x} \geq 2$ ，则 $\neg p$ 为．

查看解析
20、在特定条件下，篮球赛中进攻球员投球后，篮球的运行轨迹是开口向下的抛物线的一部分.“盖帽”是一种常见的防守手段，防守队员在篮球上升阶段将球拦截即为“盖帽”，而防守队员在篮球下降阶段将球拦截则属“违规”.对于某次投篮而言，如果忽略其他因素的影响，篮球处于上升阶段的水平距离越长，则被“盖帽”的可能性越大.收集几次篮球比赛的数据之后，某球员投篮可以简化为下述数学模型：如图所示，该球员的投篮出手点为P，篮框中心点为Q，他可以选择让篮球在运行途中经过A，B，C，D四个点中的某一点并命中Q，忽略其他因素的影响，那么被“盖帽”的可能性最大的线路是（）

A、P→A→Q B、P→B→Q C、P→C→Q D、P→D→Q

查看解析

上一页 694 695 696 697 698 下一页跳转

科普测试成绩x	科普过程性积分	人数
$90 \leq x \leq 100$	4	10
$80 \leq x < 90$	3	a
$70 \leq x < 80$	2	b
$60 \leq x < 70$	1	23
$0 \leq x < 60$	0	2