相关试卷
-
1、如图,在四棱锥中, , , , 侧面是正三角形,侧面底面 , 是的中点.
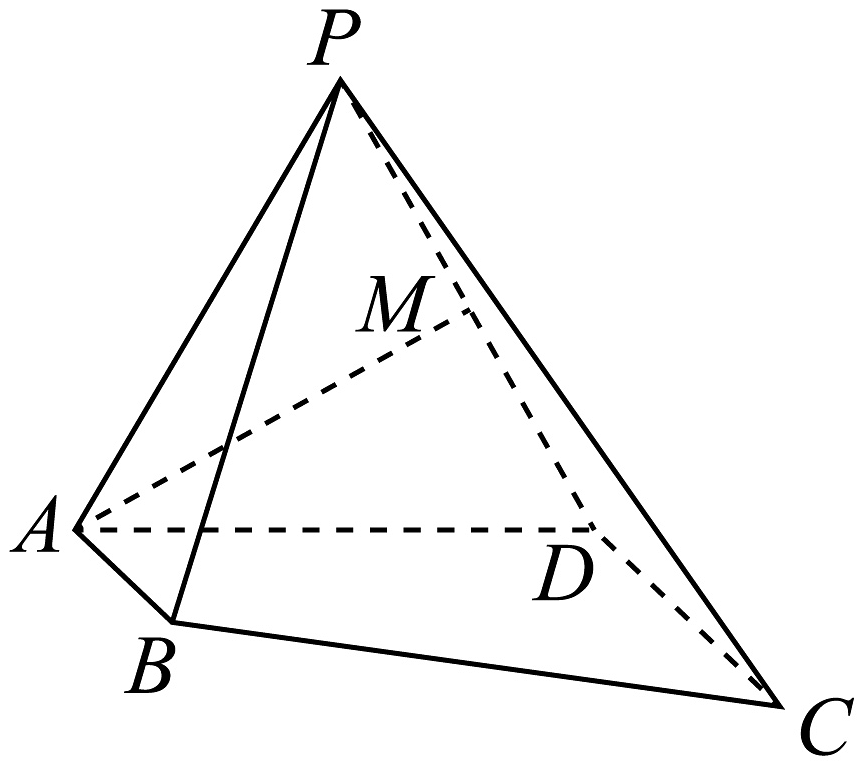 (1)、求证:平面;(2)、求平面与平面的夹角的余弦值.
(1)、求证:平面;(2)、求平面与平面的夹角的余弦值. -
2、甲、乙两选手进行乒乓球比赛,采用5局3胜制,假设每局比赛甲获胜的概率为 , 乙获胜的概率为 , 且每局比赛结果相互独立.(1)、求赛完4局且乙获胜的概率;(2)、若规定每局获胜者得2分,负者得分,记比赛结束时甲最终得分为 , 求的分布列和数学期望.
-
3、已知 , 是双曲线:( , )的左、右焦点,过作斜率为的直线交于点 , 且在第一象限,若(为坐标原点),则的离心率为.
-
4、已知 , 则.(用数字作答)
-
5、已知函数 , 则的最小正周期为.
-
6、胆式瓶创于南宋龙泉窑,康熙时期以郎红釉胆式瓶为贵.如图是18世纪的窑变红釉胆瓶,其优美的造型可看作图中曲线的一部分.已知曲线上的点到的距离与到轴的距离之积为6,若曲线上的点在第一象限,则( )
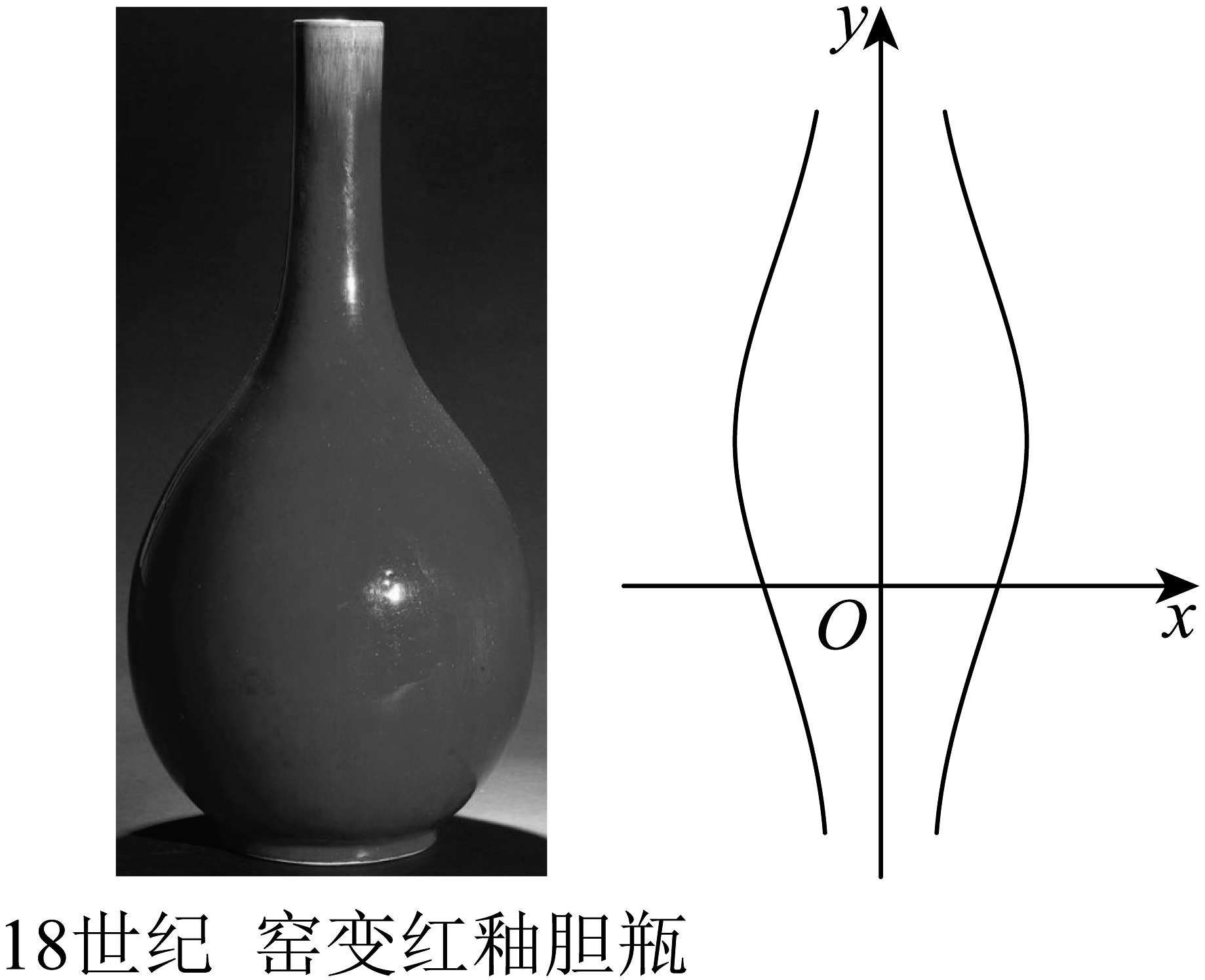 A、的最大值为 B、 C、曲线的内接矩形的面积最大值为24 D、一个胆式瓶的剖面图可近似看作曲线(),若一正四面体可在胆式瓶内任意转动(忽略胆式瓶的厚度),则该正四面体棱长的最大值为4
A、的最大值为 B、 C、曲线的内接矩形的面积最大值为24 D、一个胆式瓶的剖面图可近似看作曲线(),若一正四面体可在胆式瓶内任意转动(忽略胆式瓶的厚度),则该正四面体棱长的最大值为4 -
7、已知函数 , 则( )A、当时, B、当时, C、当且时, D、当且时,
-
8、已知直线:和圆: , 则( )A、当与圆相切时, B、当为圆的一条对称轴时, C、当时,与圆没有公共点 D、当时,被圆截得的弦长为
-
9、已知 , 则( )A、 B、 C、 D、
-
10、已知正四面体的棱长为2,点是的中点,点在正四面体表面上运动,并且总保持 , 则动点的轨迹周长为( )A、4 B、 C、 D、
-
11、已知函数是奇函数,则( )A、2 B、1 C、 D、
-
12、在中,内角 , , 所对的边分别是 , , , 若 , , 则的面积是( )A、 B、 C、 D、1
-
13、我国19岁射击运动员盛李豪在2024年巴黎奥运会上夺得了男子10米气步枪金牌,他在决赛的最后10枪成绩为10.9,10.7,10.4,10.0,10.5,9.8,10.7,9.9,10.5,10.6,则这10枪成绩的第40百分位数是( )A、10.5 B、10.45 C、10.4 D、10.25
-
14、已知 , 是两个不共线的向量,若向量 , 共线,则( )A、6 B、4 C、 D、
-
15、已知 , 则( )A、 B、1 C、 D、2
-
16、已知集合 , , 且 , 则( )A、6 B、3 C、 D、
-
17、已知分别为双曲线的左、右焦点,过的直线与圆相切于点 , 且直线与双曲线及其渐近线在第二象限的交点分别为 , 则下列说法正确的是( )A、直线是的一条渐近线 B、若 , 则的渐近线方程为 C、若 , 则的离心率为 D、若 , 则的离心率为
-
18、已知函数和 , 且 .(1)、若的最小值为 , 求实数的值.(2)、若与的图像有且仅有一个交点,求实数的取值范围.
-
19、某地为打造“生态水果庄园”,对某种果树进行调研.经调研发现,施用肥料千克时,这种果树的单株产量(单位:千克),单株施用肥料及其它成本的总投入为元.已知这种水果的市场售价大约为10元/千克,且销路畅通供不应求.记该果树的单株利润为(单位:元).(1)、求的解析式;(2)、当施用肥料为多少千克时,该果树的单株利润最大?最大利润是多少?
-
20、已知函数 .(1)、求函数的最小值(2)、当且仅当时,取得最小值,求在的值域(3)、若 , 对恒成立,求的取值范围.