相关试卷
-
1、如图,已知矩形所在平面与直角梯形所在平面垂直,在直角梯形中, , , .
 (1)、判断与是否垂直,并说明理由;(2)、求直线CN与平面所成角的余弦值.
(1)、判断与是否垂直,并说明理由;(2)、求直线CN与平面所成角的余弦值. -
2、已知圆过点和点 , 且圆心在直线上.(1)、求圆的标准方程;(2)、经过点作直线与圆相切,求直线的方程.
-
3、某学校举办了一场趣味知识竞赛,将100名参赛学生的成绩(百分制)按照[40,50),[50,60),[60,70),…,[90,100]分成6组,制成如图所示的频率分布直方图.
 (1)、求图中m的值,并估计这100名参赛学生的成绩的中位数;(2)、若从竞赛成绩在[80,90),[90,100]内的两组学生中用分层抽样的方法抽取8人,再从这8人中任意抽取2人代表学校参加竞赛,求抽取的2人中至少有1人的成绩在[90,100]内的概率.
(1)、求图中m的值,并估计这100名参赛学生的成绩的中位数;(2)、若从竞赛成绩在[80,90),[90,100]内的两组学生中用分层抽样的方法抽取8人,再从这8人中任意抽取2人代表学校参加竞赛,求抽取的2人中至少有1人的成绩在[90,100]内的概率. -
4、在正四面体中, , 则(用 , , 表示).若 , 则 .
-
5、已知事件与互斥,且 , , 则.
-
6、在长方体中, , , 为的中点,动点在长方体内(含表面),且满足 , 记动点的轨迹为 , 则( )
 A、的面积为 B、的面积为 C、当时,存在点 , 使得 D、当时,三棱锥的体积为定值
A、的面积为 B、的面积为 C、当时,存在点 , 使得 D、当时,三棱锥的体积为定值 -
7、已知圆 , 点是直线上的点,则( )A、圆上有两个点到直线的距离为2 B、圆上只有一个点到直线的距离为2 C、从点向圆引切线,切线长的最小值为 D、从点向圆引切线,切线长的最小值是
-
8、已知复数 , 则( )A、的虚部为31i B、 C、为纯虚数 D、
-
9、已知复数z满足 , 为z的共轭复数,则的最大值为( )A、7 B、9 C、25 D、49
-
10、掷两枚质地均匀的正方体骰子,记事件“第一枚骰子向上的点数为偶数”,事件“第二枚骰子向上的点数为奇数”,则( )A、与互为对立事件 B、与互斥 C、 D、
-
11、抛物线的焦点坐标为( )A、 B、 C、 D、
-
12、甲、乙两人独立地攻克一道难题,已知两人能攻克的概率分别是 , , 则该题被攻克的概率为( )A、 B、 C、 D、
-
13、设 , 则z在复平面内所对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
14、函数的零点所在的区间可能是( )A、 B、 , C、 , D、 ,
-
15、已知点是双曲线上任意一点.(1)、求证:点P到双曲线C的两条渐近线的距离的乘积是一个常数;(2)、已知点 , 求的最小值.
-
16、如图,矩形是圆柱的轴截面,分别是上、下底面圆周上的点,且 .
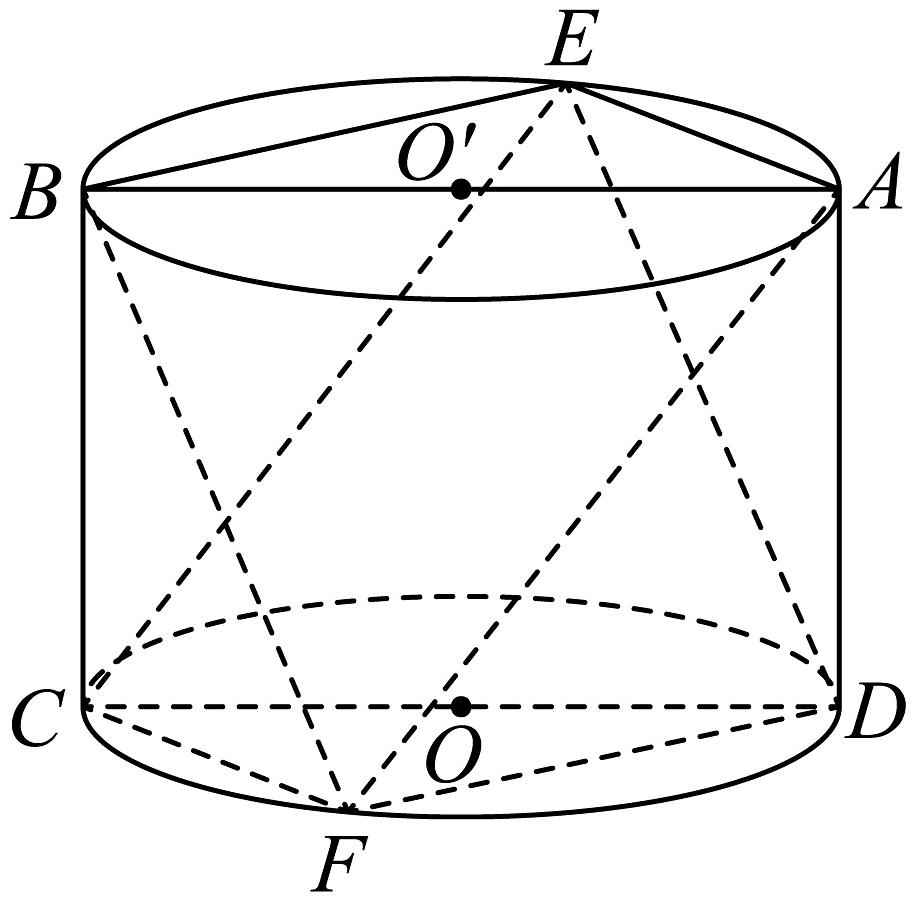 (1)、求证:;(2)、若四边形为正方形,求平面与平面夹角的正弦值
(1)、求证:;(2)、若四边形为正方形,求平面与平面夹角的正弦值 -
17、已知分别是椭圆的右顶点,上顶点和右焦点,若过三点的圆恰与轴相切,则的离心率为 .
-
18、在梯形中, , 则( )A、 B、 C、 D、
-
19、若是方程的实数解,则称是函数与的“复合稳定点”.若函数且与有且仅有两个不同的“复合稳定点”,则的取值范围为( )A、 B、 C、 D、
-
20、造型
 可以看作图中曲线C的一部分,已知C过坐标原点O,且C上的点满足横坐标大于 , 到点的距离与到定直线的距离之积为
可以看作图中曲线C的一部分,已知C过坐标原点O,且C上的点满足横坐标大于 , 到点的距离与到定直线的距离之积为 (1)、求a的值;(2)、当点在C上时,求证:(3)、如图,过点F作两条互相垂直的弦,分别交曲线C于 , , , , 其中 , 求四边形面积的最小值.
(1)、求a的值;(2)、当点在C上时,求证:(3)、如图,过点F作两条互相垂直的弦,分别交曲线C于 , , , , 其中 , 求四边形面积的最小值.