版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、如图，二面角 $α - l - β$ 等于135°， $A$ ， $B$ 是棱 $l$ 上两点， $B D$ ， $A C$ 分别在半平面 $α$ ， $β$ 内， $A C ⊥ l$ ， $B D ⊥ l$ ，且 $A B = A C = 2$ ， $B D = \sqrt{2}$ ，则 $C D =$ （）

A、 $2 \sqrt{3}$ B、 $2 \sqrt{2}$ C、 $\sqrt{14}$ D、4

查看解析
2、在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 是正方形， $E$ 为 $P D$ 中点，若 $\vec{P A} = \vec{a}, \vec{P B} = \vec{b}, \vec{P C} = \vec{c}$ ，用 $\vec{a}, \vec{b}, \vec{c}$ 表示 $\vec{B E}$ ，则 $\vec{B E} =$ （）

A、 $\frac{1}{2} \vec{a} + \frac{3}{2} \vec{b} - \frac{1}{2} \vec{c}$ B、 $\frac{1}{2} \vec{a} - \frac{3}{2} \vec{b} + \frac{1}{2} \vec{c}$ C、 $\frac{1}{2} \vec{a} + \frac{1}{2} \vec{b} - \frac{3}{2} \vec{c}$ D、 $\frac{1}{2} \vec{a} - \frac{1}{2} \vec{b} + \frac{3}{2} \vec{c}$

查看解析
3、定义在 $R$ 上的函数 $g (x)$ 和二次函数 $h (x)$ 满足： $g (x) + 2 g (- x) = e^{x} + \frac{2}{e^{x}} - 9$ ， $h (- 2) = h (0) = 1$ ， $h (- 3) = - 2$ ．
（1）求 $g (x)$ 和 $h (x)$ 的解析式；
（2）若对于 $x_{1}$ 、 $x_{2} \in [- 1, 1]$ ，均有 $h (x_{1}) + a x_{1} + 5 \geq g (x_{2}) + 3 - e$ 成立，求 $a$ 的取值范围；
（3）设 $f (x) = \{\begin{array}{l} g (x), x > 0 \\ h (x), x \leq 0 \end{array}$ ，在（2）的条件下，讨论方程 $f [f (x)] = a + 5$ 的解的个数．

查看解析
4、已知 $- 2 < x - y < 0$ ， $1 < 2 x + y < 3$ ．

(1)、分别求x与y的取值范围；

(2)、求8x + y的取值范围．

查看解析
5、已知函数 $f (x) = sin (2 x + \frac{π}{4})$ ．

(1)、求 $f (x)$ 图象的对称轴方程；

(2)、求 $f (x)$ 在区间 $[0, 2 π]$ 上的单调递增区间．

查看解析
6、下列函数中，与y＝x是同一个函数的是（）

A、 $y = \sqrt[3]{x^{3}}$ B、 $y = \sqrt{x^{2}}$ C、 $y = \ln e^{x}$ D、 $y = 10^{\lg x}$

查看解析
7、正实数 $a$ 、 $b$ 满足 $a + \frac{9}{b} = 1$ ，若不等式 $\frac{1}{a} + b \geq - x^{2} + 4 x + 18 - m$ 对任意正实数 $a$ 、 $b$ 以及任意实数 $x$ 恒成立，则实数 $m$ 的取值范围是（）

A、 $[3, + \infty)$ B、 $[3, 6]$ C、 $[6, + \infty)$ D、 $(- \infty, 6]$

查看解析
8、数学中一般用 $\min \{a, b\}$ 表示a、b中的较小值，关于函数 $f (x) = \min \{\sin x + \sqrt{3} \cos x, \sin x - \sqrt{3} \cos x\}$ 有如下四个命题：
① $f (x)$ 的最小正周期为 $2 π$ ；② $f (x)$ 的图像关于直线 $x = \frac{3 π}{2}$ 对称；
③ $f (x)$ 的值域为 $[- 2, 2]$ ；④ $f (x)$ 在区间 $(- \frac{π}{6}, \frac{π}{4})$ 上单调递增.
其中真命题的个数为（）

A、1个 B、2个 C、3个 D、4个

查看解析
9、一家商店使用一架两臂不等长的天平称黄金．一位顾客到店里购买 $10 g$ 黄金，售货员现将 $5 g$ 的砝码放在天平的左盘中，取出 $x g$ 黄金放在天平右盘中使天平平衡；将天平左右盘清空后，再将 $5 g$ 的砝码放在天平右盘中，再取出 $y_{g}$ 黄金放在天平的左盘中，使天平平衡；最后将两次称得的黄金交给顾客．则（）

A、 $x + y > 10$ B、 $x + y = 10$ C、 $x + y < 10$ D、以上都有可能

查看解析
10、关于函数 $y ＝ t a n (2 x - \frac{π}{3})$ ，下列说法正确的是(　　)

A、是奇函数 B、在区间 $(0, \frac{π}{3})$ 上单调递减 C、 $(\frac{π}{6}, 0)$ 为其图象的一个对称中心 D、最小正周期为π

查看解析
11、函数 $f (x) = \frac{\lg (x + 1)}{x^{2} + 2 x}$ 的定义域为（）

A、 $[- 1, + \infty)$ B、 $(- 1, 0) \cup (0, + \infty)$ C、 $(- 1, + \infty)$ D、 $[- 1, 0) \cup (0, + \infty)$

查看解析
12、设 $x \in R$ ，则“ $|x + 1| < 1$ ”是“ $\frac{1}{x} < \frac{1}{2}$ ”的（）条件

A、充分不必要 B、必要不充分 C、充分必要 D、既不充分也不必要

查看解析
13、已知全集 $U = {0,1, 2,3, 4}$ ， $A = {1,3}$ ， $B = {0,1, 2,4}$ ，则( $∁_{U} A$ ) $\cap B$ =（）

A、{ $0$ } B、{ $2$ } C、{ $0, 2$ } D、{ $0,2, 4$ }

查看解析
14、已知函数 $f (x) = x^{2} + (1 - 2 a) x - a \ln x (a \in R)$ ．

(1)、当 $a = 1$ 时，求函数 $f (x)$ 的单调递减区间；

(2)、求函数 $f (x)$ 在 $[1, 2]$ 上的最小值．

查看解析
15、电力公司从某小区抽取100户居民用户进行12月用电量调查，发现他们的月用电量都在 $50 \sim 650 kW \cdot h$ 之间，进行适当分组后（每组为左闭右开的区间），画出频率分布直方图如图所示.

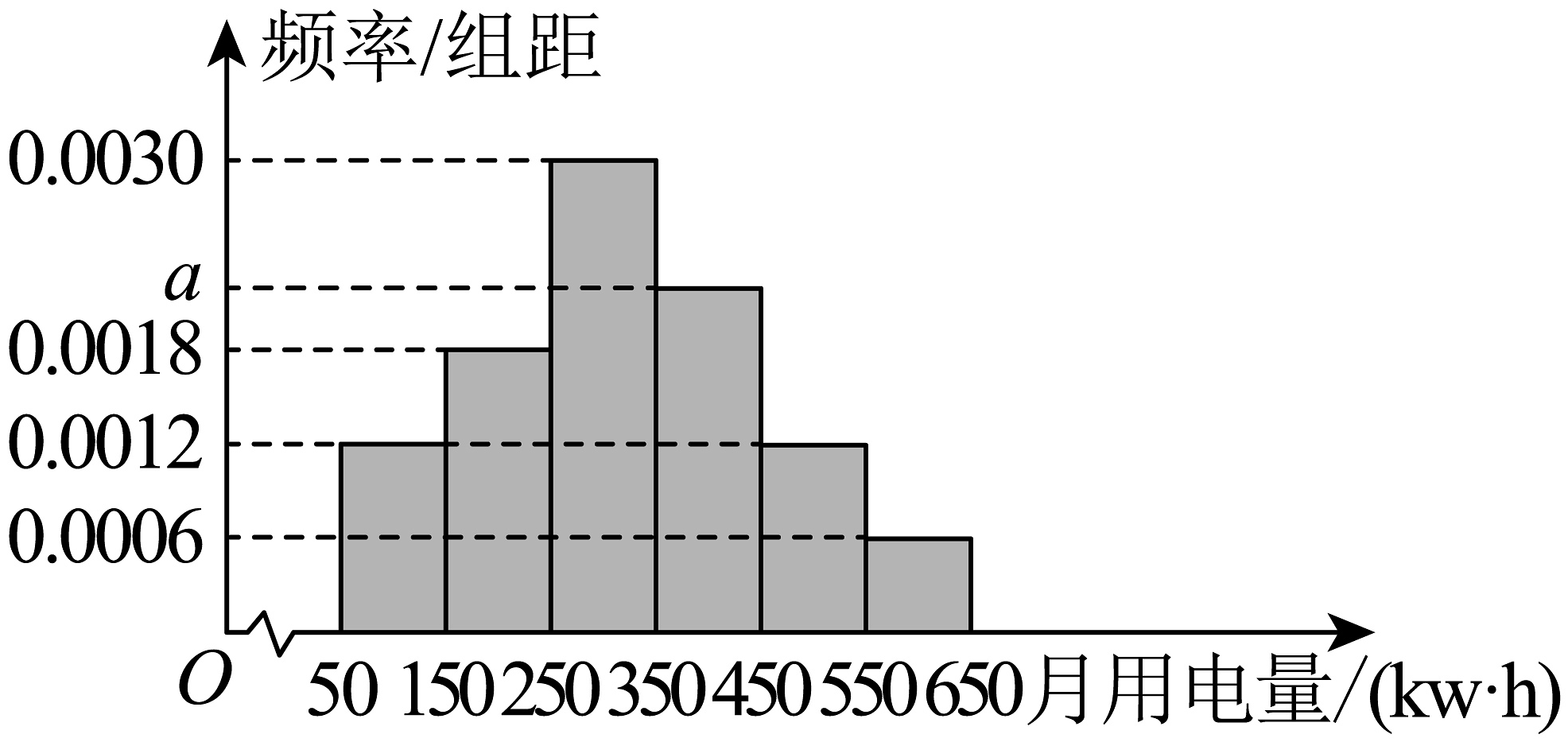(1)、求 $a$ 的值及这100户的用电量的平均数；

(2)、力公司拟对用电量超过 $M (kW \cdot h)$ 的家庭的电器进行检测，若 $M$ 恰好为第71百分位数，求 $M$ .

查看解析
16、在三棱锥 $P - A B C$ 中，平面 $P A B ⊥$ 平面 $A B C, A B = 2 \sqrt{3}$ ， $B C = 2, A C = 4, △ P A B$ 是等腰直角三角形， $P A = P B$ .

(1)、求证： $P A ⊥$ 平面 $P B C$ ；

(2)、求异面直线 $P B$ 与 $A C$ 的夹角的余弦值；

(3)、设点 $T$ 是三棱锥 $P - A B C$ 外接球上一点，求 $T$ 到平面 $P B C$ 距离的最大值.

查看解析
17、如图，两个正四棱锥的底面都为正方形 $A B C D$ ，顶点 $M, N$ 位于底面两侧， $|A B| = 2, A M ⊥ A N$ ．记正四棱锥 $M - A B C D$ 的体积为 $V_{1}$ ，正四棱锥 $N - A B C D$ 的体积为 $V_{2}$ ．

(1)、求 $V_{1} + V_{2}$ 的最小值；

(2)、若 $V_{1} = 2 V_{2}$ ，求直线 $A M$ 与平面 $B C N$ 所成角的正弦值．

查看解析
18、某中学体育组对高三的800名男生做了单次引体向上的测试，得到了如图所示的频率分布直方图（引体向上个数只记整数）．体育组为进一步了解情况，组织了两个研究小组．

(1)、第一小组决定从单次完成1~15个引体向上的男生中，采用比例分配的分层随机抽样的方法抽取22人进行全面的体能测试．
①在单次完成6~10个引体向上的所有男生中，男生甲被抽到的概率是多少？
②该小组又从这22人中抽取3人进行个别访谈，记抽到“单次完成引体向上1~5个”的人数为随机变量X，求X的分布列；

(2)、第二小组从学校学生的成绩与体育锻炼相关性角度进行研究，得到了这800人的学业成绩与体育成绩之间的 $2 \times 2$ 列联表．
体育成绩
学业成绩
合计
优秀
不优秀
不优秀
200
400
600
优秀
100
100
200
合计
300
500
800
根据小概率值 $a = 0.005$ 的独立性检验，分析体育锻炼是否与学业成绩有关？
参考公式：独立性检验统计量 $χ^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$ ．
临界值表：
α
0.1
0.05
0.01
0.005
0.001
$x_{α}$
2.706
3.841
6.635
7.879
10.828

查看解析
19、已知在数列 $\{a_{n}\}$ 中， $a_{1} = 1, a_{n + 1} = \frac{2 (n + 1)}{n} a_{n} \cdot (n \in N^{*})$

(1)、求数列 $\{a_{n}\}$ 的通项公式；

(2)、若数列 $\{b_{n}\}$ 的通项公式 $b_{n} = \frac{a_{n}}{n}$ 在 $b_{k}$ 和 $b_{k + 1}$ 之间插入k个数，使这 $k + 2$ 个数组成等差数列，将插入的k个数之和记为 $c_{k}$ ，其中 $k = 1$ ， 2，…，n，求数列 $\{c_{n}\}$ 的前n项和．

查看解析
20、已知函数 $f (x) = 2 \sin (ω x + ϕ) (ω > 0 ， | ϕ | < π)$ 的部分图象如下图所示，且 $A (\frac{π}{2} ， 1) ， B (π ， - 1)$ ，则 $ϕ$ 的值为．

查看解析

上一页 568 569 570 571 572 下一页跳转

体育成绩	学业成绩		合计
体育成绩	优秀	不优秀	合计
不优秀	200	400	600
优秀	100	100	200
合计	300	500	800

α	0.1	0.05	0.01	0.005	0.001
$x_{α}$	2.706	3.841	6.635	7.879	10.828