相关试卷
-
1、已知 , 且函数 .(1)、化简;(2)、若 , 求和的值.
-
2、为庆祝中国共产党第二十次代表大会胜利闭幕,某高中学校在学生中开展了“学精神,悟思想,谈收获”的二十大精神宣讲主题活动.为了解该校学生参加主题学习活动的具体情况,校团委利用分层抽样的方法从三个年级中抽取了260人进行问卷调查,其中高一、高二年级各抽取了85人.已知该校高三年级共有720名学生,则该校共有学生人.
-
3、如图所示,在复平面内,网格中的每个小正方形的边长都为1,点A,B对应的复数分别是 , 则 .

-
4、如图,三棱柱ABC-A1B1C1中,底面三角形A1B1C1是正三角形,E是BC的中点,则下列叙述错误的是( )
 A、CC1与B1E是异面直线 B、C1C与AE共面 C、AE与B1C1是异面直线 D、AE与B1C1所成的角为60°
A、CC1与B1E是异面直线 B、C1C与AE共面 C、AE与B1C1是异面直线 D、AE与B1C1所成的角为60° -
5、下列函数中,周期为π,且在区间上单调递增的是( )A、 B、 C、 D、
-
6、某校对学生在寒假中参加社会实践活动的时间(单位:小时)进行调查,并根据统计数据绘制了如图所示的频率分布直方图,其中实践活动时间的范围是[9,14],数据的分组依次为:[9,10),[10,11),[11,12),[12,13),[13,14].已知活动时间在[9,10)内的人数为300,则活动时间在[11,12)内的人数为( )
 A、600 B、800 C、1000 D、1200
A、600 B、800 C、1000 D、1200 -
7、若是不在同一平面内的三条线段,则过它们中点的平面和直线的位置关系是 ( )A、平行 B、相交 C、在此平面内 D、平行或相交
-
8、如图,正三棱柱的底面是边长为3的正三角形,侧棱 , 一小虫从点A途经三个侧面爬到点 , 则小虫爬行的最短距离为( )
 A、4 B、5 C、 D、
A、4 B、5 C、 D、 -
9、如图是古希腊数学家特埃特图斯用来构造无理数的图形,图中四边形ABCD的对角线相交于点O,若 , 则( )
 A、1 B、 C、 D、5
A、1 B、 C、 D、5 -
10、已知向量 , 不共线,且 , , 若与反向共线,则实数的值为( )A、1 B、 C、 D、-2
-
11、在平面直角坐标系中,若角的终边经过点 , 则( )A、 B、 C、 D、
-
12、已知动点到点的距离比它到直线的距离小 , 记动点的轨迹为 .(1)、求轨迹的方程.(2)、直线与分别与轨迹交于点和点(与同向),且 , 线段与交于点 , 线段与的中点分别为 .
(ⅰ)求证:三点共线;
(ⅱ)若 , , 求四边形ABCD的面积.
-
13、如图,在圆柱中,四边形ABCD是其轴截面,EF为的直径, , , .
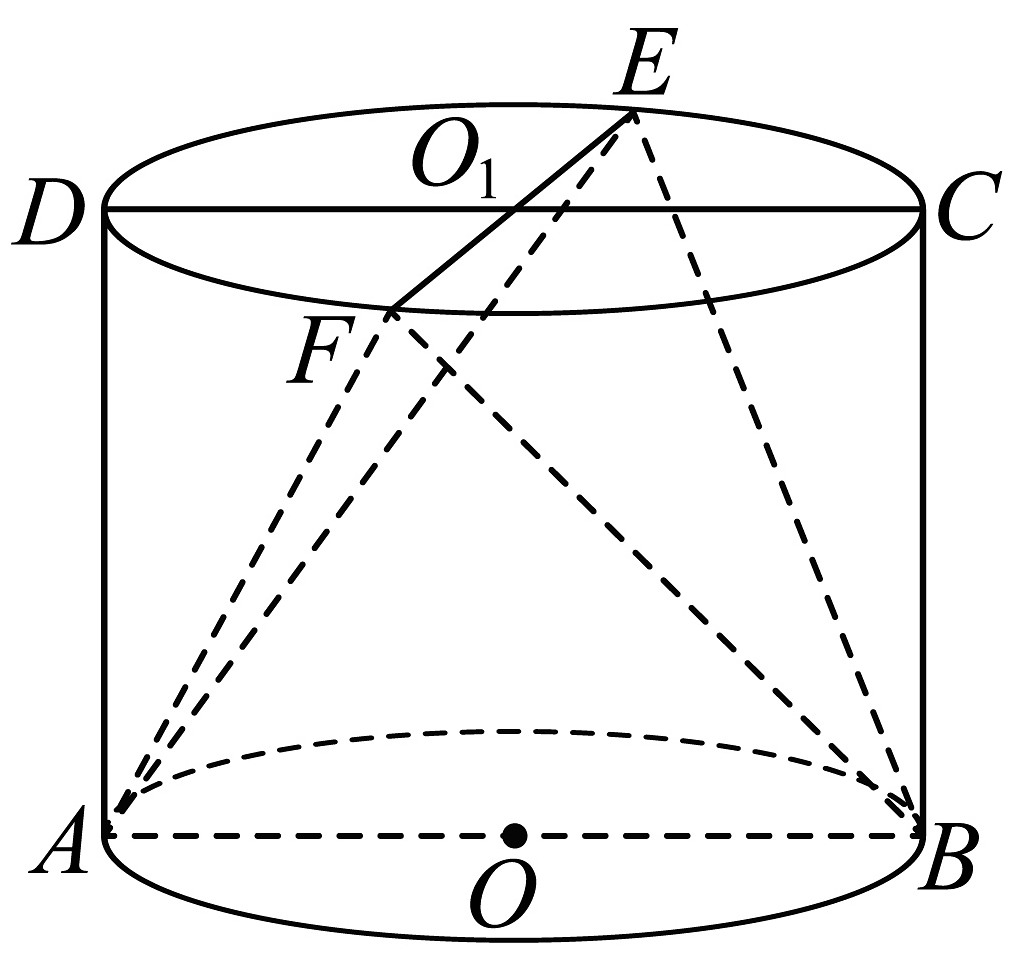 (1)、求证:;(2)、若四面体ABEF的体积为 , 求二面角平面角的余弦值.
(1)、求证:;(2)、若四面体ABEF的体积为 , 求二面角平面角的余弦值. -
14、为了切实加强学校体育工作,促进学生积极参加体育锻炼,养成良好的锻炼习惯,某高中学校计划优化课程,增加学生体育锻炼时间,提高体质健康水平,某体质监测中心抽取了该校10名学生进行体质测试,得到如下表格:
序号i
1
2
3
4
5
6
7
8
9
10
成绩(分)
38
41
44
51
54
56
58
64
74
80
记这10名学生体质测试成绩的平均分与方差分别为 , , 经计算 , .
(1)、规定体质测试成绩低于50分为不合格,从这10名学生中任取3名,记体质测试成绩不合格的人数为X,求X的分布列;(2)、经统计,高中生体质测试成绩近似服从正态分布 , 用 , 的值分别作为 , 的近似值,若监测中心计划从全省抽查10000名高中生进行体质测试,记这10000名高中生的体质测试成绩恰好落在区间的人数为Y,求Y的数学期望 .附:若 , 则 , , .
-
15、在中,内角A,B,C所对的边分别为a,b,c,已知 .(1)、求B;(2)、若 , 且满足 , 求的周长.
-
16、已知函数.若函数有七个不同的零点,则实数的取值范围是.
-
17、已知是椭圆的两个焦点,点M在C上,则的最大值为 .
-
18、设函数 , , 若是奇函数,则 .
-
19、已知四面体中, , , , 为四面体外接球的球心,则下列说法中正确的是( )A、若 , 则平面 B、若 , 则的取值范围是 C、若 , 则的取值范围是 D、若 , 直线与所成的角为 , 则四面体外接球的表面积为
-
20、随机事件A、B满足 , , , 下列说法正确的是( )A、事件与事件B相互独立 B、 C、 D、