相关试卷
-
1、若实数 , 满足 , 则的最大值为.
-
2、已知函数的图象过点 , 若在内有4个零点,则a的取值范围为 .
-
3、已知定义在上的函数的值域是 , 则函数的值域是.
-
4、事件、互斥,若 , , 则.
-
5、如图,棱长为2的正方体中,为棱的中点,为正方形内一个动点(包括边界),且平面 , 则下列说法正确的有( )
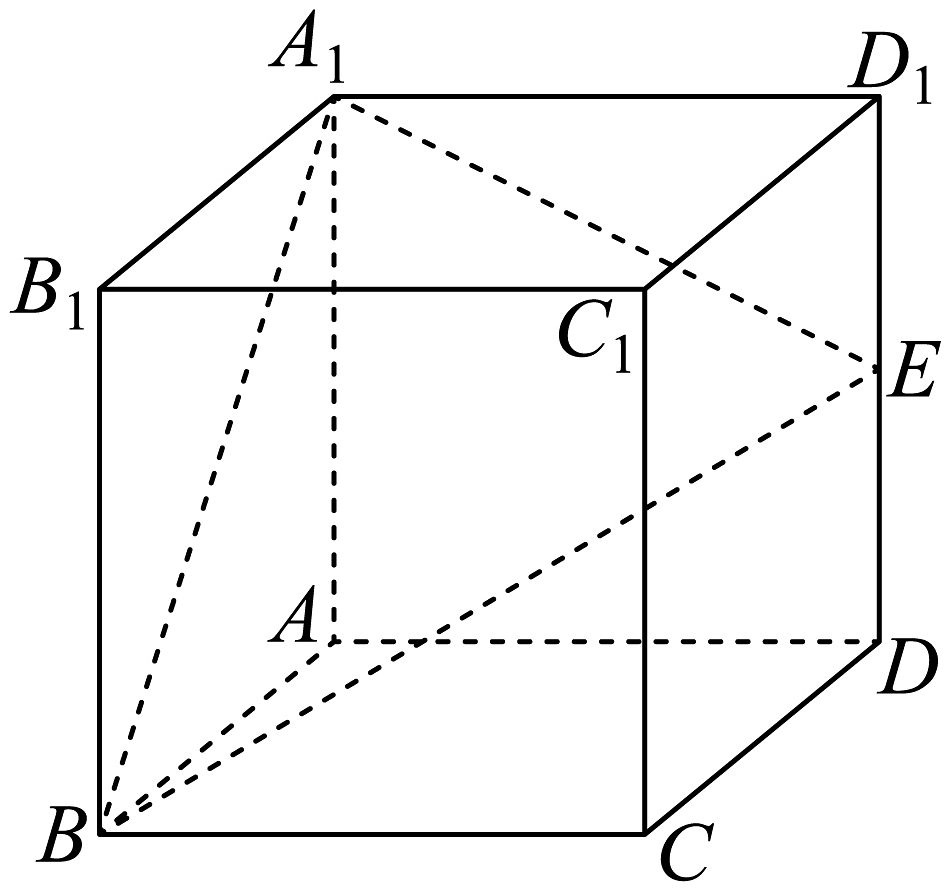 A、动点轨迹的长度为 B、与不可能垂直 C、直线与平面所成角正弦值的最小值为 D、当三棱锥的体积最大时,其外接球的表面积为
A、动点轨迹的长度为 B、与不可能垂直 C、直线与平面所成角正弦值的最小值为 D、当三棱锥的体积最大时,其外接球的表面积为 -
6、下列命题为真命题的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则
-
7、已知函数 , 若关于的不等式的解集中有且仅有个整数,则实数的取值范围为( )A、 B、 C、 D、
-
8、已知 , 现将函数的图象向右平移个单位后得到函数的图象,若存在 , 使得函数与图象的对称中心完全相同,则满足题意的的个数为( )A、 B、 C、 D、
-
9、如图两点在河的同侧,且、两点均不可到达.现需测、两点间的距离,测量者在河对岸选定两点、 , 测得 , 同时在、两点分别测得 , , , 则、两点间的距离为( )
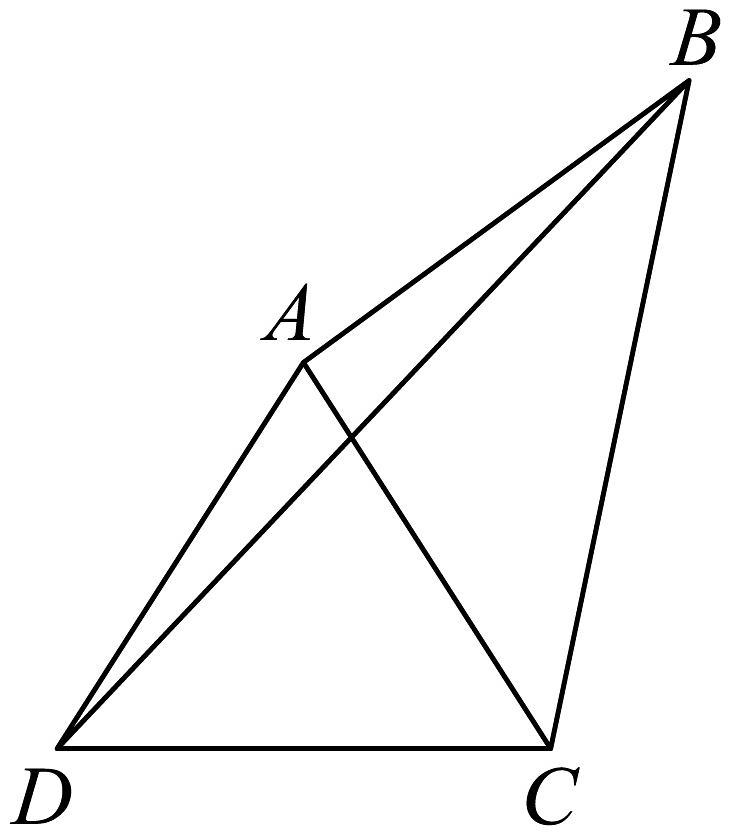 A、 B、 C、 D、
A、 B、 C、 D、 -
10、已知 , 且 , 则( )A、2或8 B、或8 C、8 D、64
-
11、已知不等式的解集为 , 则的解集为( )A、 B、 C、 D、
-
12、甲、乙两人独立破译一份密码,已知两人能破译的概率分别是 , , 则恰有一人成功破译的概率为( )A、 B、 C、 D、
-
13、已知 , 则=( )A、 B、 C、 D、
-
14、已知复数 , , 则复数在复平面内对应点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
15、下列函数中,定义域为的函数是( )A、 B、 C、 D、
-
16、若对于任意整数 , , 均有 , 则称数列为数列.(1)、设各项均为正整数且公差不为0的等差数列为数列, , 求;(2)、证明:当时,数列为数列;(3)、证明:若数列的各项均为正数,当时(其中 , 为常数),数列不是数列.
-
17、已知双曲线的实轴长为 , 离心率为.(1)、求双曲线的标准方程:(2)、过点的直线与的左、右两支分别交于 , 两点,点 , 直线与直线交于点.
(i)证明:直线的斜率为定值;
(ii)记 , 分别为 , 的面积,求的取值范围.
-
18、已知函数 , .(1)、若 , 求图象在点处的切线方程;(2)、若函数在上的最小值是 , 求的值.
-
19、记的内角 , , 的对边分别为 , , , 且 .(1)、求;(2)、若 , 且边上的高为 , 求的周长.
-
20、两个不透明的袋子中均装有1个红球,2个白球,2个黑球(除颜色外,质地大小均相同),从两个袋子中同时取出1个球(取出的球不放回袋中),若两球颜色相同,则记1分,否则记0分,则取球5次后,总得分大于2的概率为.