相关试卷
-
1、十六世纪中叶,英国数学家雷科德在《砺智石》一书中首先把“=”作为等号使用,后来英国数学家哈利奥特首次使用“<”和“>”符号,并逐渐被数学届接受,不等号的引入对不等式的发展影响深远.已知 , , 均为实数,且满足 , 那么下列选项中一定成立的是( )A、 B、 C、 D、
-
2、已知集合 , 则( )A、 B、 C、 D、
-
3、函数的图象的一个对称中心是( )A、 B、 C、 D、
-
4、对于定义域为的函数,如果存在区间 , 同时满足下列两个条件:
①在区间上是单调的;
②当定义域是时,的值域也是 . 则称是函数的一个“黄金区间”.
(1)请证明:函数不存在“黄金区间”.
(2)已知函数在上存在“黄金区间”,请求出它的“黄金区间”.
(3)如果是函数的一个“黄金区间”,请求出的最大值.
-
5、如图,矩形所在的平面垂直于平面 , 为的中点, , , , .
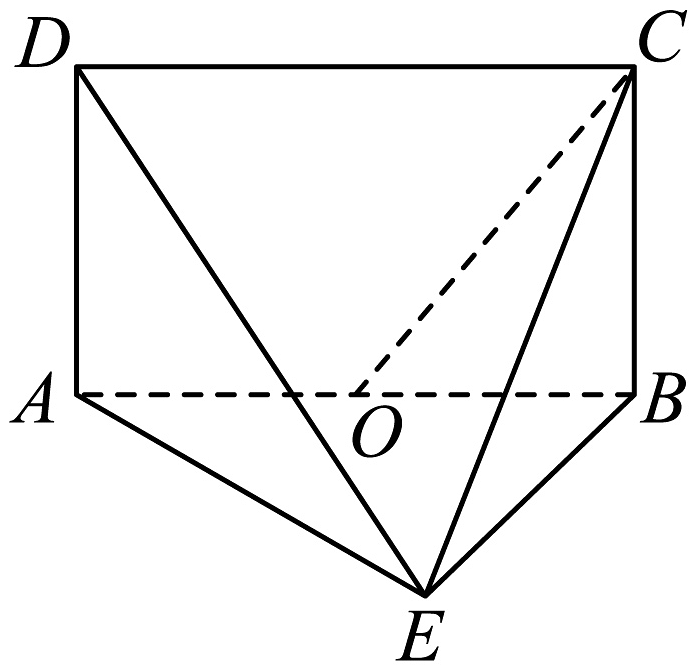
(1)求异面直线与所成角的余弦值;
(2)求二面角的正弦值.
-
6、已知圆经过点 , 且圆与轴相切.(1)、求圆的方程;(2)、设是圆上的动点,点的坐标为 , 求线段CP的中点的轨迹方程.
-
7、直线被圆截得的弦长为 .
-
8、某校1000名学生在高一测试中数学成绩的频率分布直方图如图所示(同一组中的数据用该组区间的中点值作代表),则( )
 A、 B、约有200人的成绩不低于110分 C、约有60人的成绩低于70分 D、本次考试的平均分约为93.6分
A、 B、约有200人的成绩不低于110分 C、约有60人的成绩低于70分 D、本次考试的平均分约为93.6分 -
9、已知全集 , , , 则( )A、 B、 C、 D、
-
10、已知是定义在上的单调函数,则a的取值范围是( )A、 B、 C、 D、
-
11、已知幂函数满足 .(1)、求函数的解析式;(2)、若函数 , 是否存在实数 , (),使函数在上的值域为?若存在,求出实数的取值范围,若不存在,请说明理由.
-
12、某公司为了节约资源,研发了一个从生活垃圾中提炼煤油的项目.该项目的月处理成本(元)与月处理量(吨)之间的函数关系可以近似地表示为: , 每处理一吨生活垃圾,可得到的煤油的价值为 200 元,若该项目不能获利,政府将给予补贴.(1)、当时,判断该项目能否获利.如果获利,求出最大利润; 如果不能获利,则政府每月最多需要补贴多少元,才能使该项目不亏损?(2)、该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
-
13、已知是定义在 上的偶函数,且时, .(1)、求 , ;(2)、求函数的表达式;(3)、判断并证明函数在区间上的单调性.
-
14、已知函数的定义域为 , , 对任意两个不等的实数 , 都有 , 则不等式的解集为 .
-
15、已知集合 , 则集合A真子集个数为(填数字)
-
16、下列各组函数中,两个函数是同一函数的有( ).A、与 B、与 C、与 D、与
-
17、已知函数在区间上递减,且当时,有 , 则实数t的取值范围是( )A、 B、 C、 D、
-
18、历史上第一个给出函数一般定义的是19世纪德国数学家狄利克雷(Dirichlet),当时数学家们处理的大部分数学对象都没有完全的严格的定义,数学家们习惯借助于直觉和想象来描述数学对象,狄利克雷在1829年给出了著名函数:(其中为有理数集,为无理数集),狄利克雷函数的出现表示数学家们对数学的理解发生了深刻的变化,数学的一些“人造”特征开始展现出来,这种思想也标志着数学从研究“算”转变到了研究“概念、性质、结构”.一般地,广义的狄利克雷函数可定义为:(其中 , 且),以下对说法错误的是( )A、定义域为 B、当时,的值域为;当时,的值域为 C、为偶函数 D、在实数集的任何区间上都不具有单调性
-
19、若均大于零,且 , 则的最小值为( )A、 B、 C、 D、
-
20、若函数是上的减函数,则的取值范围为( )A、 B、 C、 D、