相关试卷
-
1、(1)求值:;
(2)求值:.
(3)解方程:.
-
2、依法纳税是每个公民应尽的义务,个人取得的所得应依照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税).2019年1月1日起我国正式执行新个税法,个税的部分税率级距进一步优化调整,扩大3%、10%、20%三档低税率的级距,减税向中低收入人群倾斜.税率与速算扣除数见下表:
级数
全年应纳税所得额所在区间
税率(%)
速算扣除数
1
[0,36000]
3
0
2
(36000,144000]
10
2520
3
(144000,300000]
20
16920
4
(300000,420000]
25
31920
5
(420000,660000]
30
小华的全年应纳税所得额100000元,则全年应缴个税为元.还有一种速算个税的办法:全年应纳税所得额对应档的税率对应档的速算扣除数,即小华全年应缴个税为元.按照这一算法,当小李的全年应纳税所得额为200000元时,全年应缴个税为 , 表中的.
-
3、已知函数满足 , 则函数值域为.
-
4、关于的方程有实数根,则实数的取值范围为.
-
5、已知函数 , 若关于的方程有8个不同的实数根,则实数的取值范围为( )A、 B、 C、 D、
-
6、已知函数的定义域为 , 则的定义域为( )A、 B、 C、 D、
-
7、如图,在四棱锥中,底面是边长为2的正方形,底面 , , 为的中点,为的中点,解答以下问题:
 (1)、证明:直线平面;(2)、求点到平面的距离.
(1)、证明:直线平面;(2)、求点到平面的距离. -
8、函数的图象关于坐标原点成中心对称图形的充要条件是函数为奇函数,有同学发现可以将其推广为:函数的图象关于点成中心对称图形的充要条件是函数为奇函数.已知函数 , 请完成下列问题.(1)、当 , 时,求函数图象的对称中心点坐标;(2)、在(1)的条件下,若 , 关于的方程有三个不同的实数解,求实数的取值范围;(3)、若 , 证明:.
-
9、某企业生产 , 两种产品,根据市场调查和预测,产品的利润(万元)与投资额(万元)成正比,其关系如图(1)所示;产品的利润(万元)与投资额(万元)的算术平方根成正比,其关系如图(2)所示,
 (1)、分别将 , 两种产品的利润表示为投资额的函数;(2)、该企业已筹集到万元资金,并全部投入 , 两种产品的生产,问:怎样分配这万元投资,才能使企业获得最大利润?其最大利润约为多少万元?
(1)、分别将 , 两种产品的利润表示为投资额的函数;(2)、该企业已筹集到万元资金,并全部投入 , 两种产品的生产,问:怎样分配这万元投资,才能使企业获得最大利润?其最大利润约为多少万元? -
10、已知不等式的解集为 .(1)、解不等式;(2)、若 , 当时,解关于的不等式 .
-
11、已知全集为 , 集合 , 集合 , 集合 .(1)、求集合;(2)、在下列条件中任选一个,补充在下面问题中作答.
①;②;③ . 若__________,求实数的取值范围.
注:如果选择多个条件分别解答,则按第一个解答计分.
-
12、函数的最小值为
-
13、已知方程 , 则=.
-
14、写出命题的否定:
-
15、定义 , 已知函数 , , 则函数的零点个数可能为( )A、1个 B、2个 C、3个 D、4个
-
16、已知 , 则下列说法正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则
-
17、设函数 , , 若对任意的 , 存在 , 使得 , 则实数的取值范围是( )A、 B、 C、 D、
-
18、函数的图象可能是( )A、
 B、
B、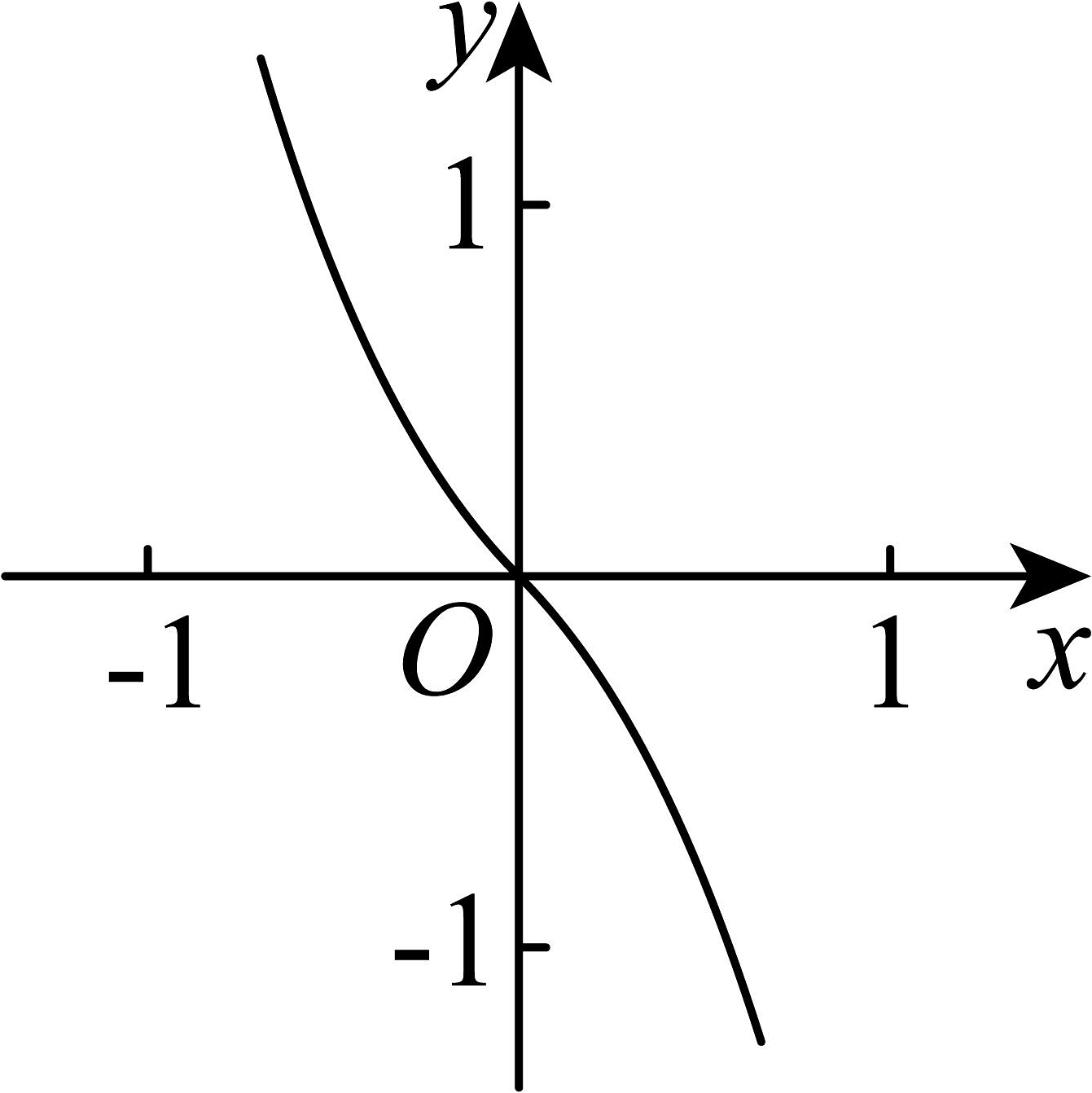 C、
C、 D、
D、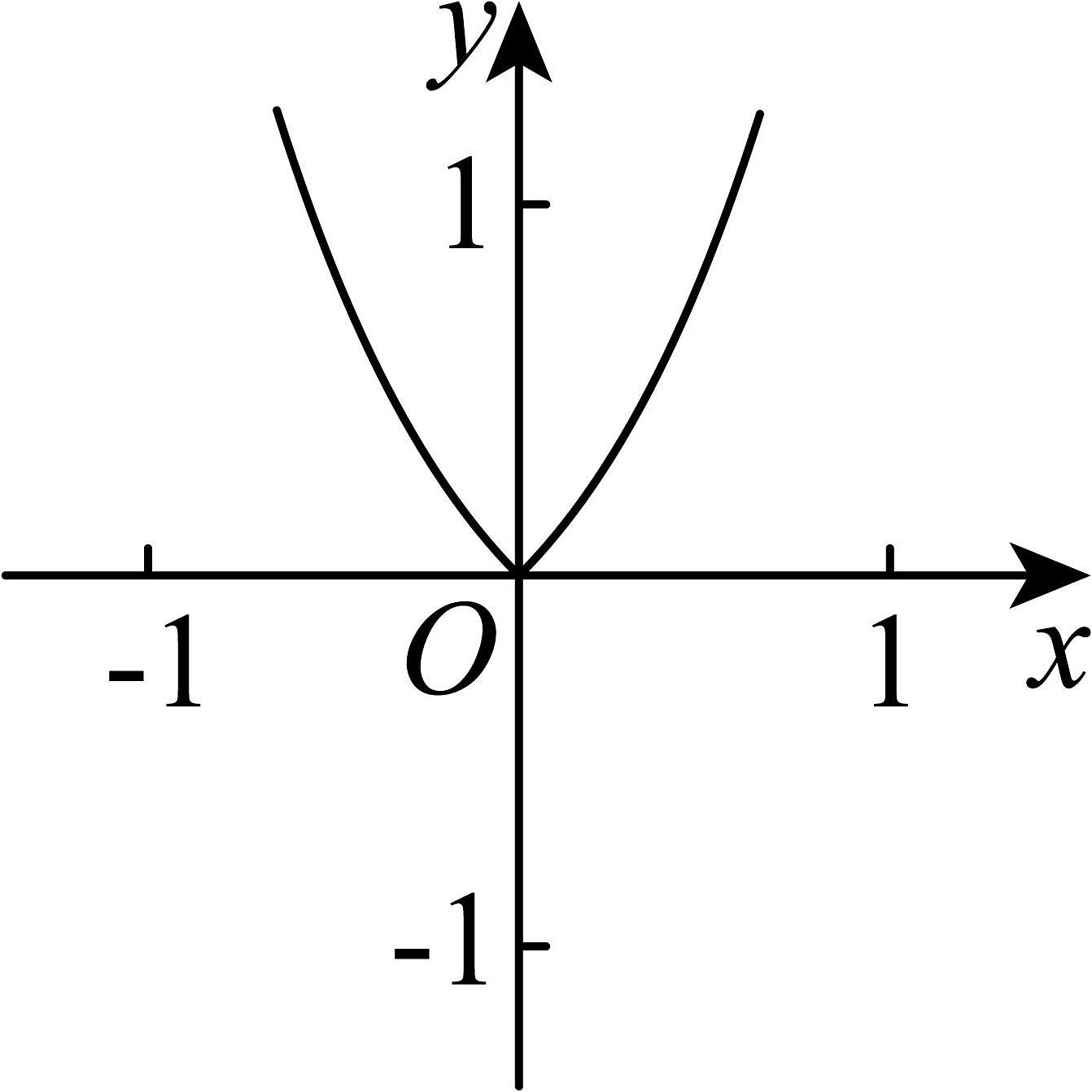
-
19、下列函数与是同一个函数的是( )A、 B、 C、 D、
-
20、已知: , : , 则是的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分又不必要条件