版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、函数 $f (x) = \frac{1}{\sqrt{x - 3}}$ 的定义域为（）

A、 $[3, + \infty)$ B、 ${x | x \in R}$ C、 $(3, + \infty)$ D、 $(- 3, + \infty)$

查看解析
2、已知全集 $U = \{1, 2, 3, 4, 5\}$ ， $M = \{1, 2, 3\}$ ， $N = \{3, 4\}$ ， $(∁_{U} M) \cup N =$ （）

A、 $\{4\}$ B、 $\{4, 5\}$ C、 $\{3, 4, 5\}$ D、 $\{1, 2, 3, 4, 5\}$

查看解析
3、如图，平面 $A B C D ⊥$ 平面 $A B E F$ ，四边形 $A B E F$ 为正方形，四边形 $A B C D$ 为菱形， $∠ D A B = 60 °$ ，则直线 $A C, F B$ 所成角的余弦值为（）

A、 $\frac{\sqrt{6}}{3}$ B、 $\frac{\sqrt{5}}{3}$ C、 $\frac{\sqrt{10}}{4}$ D、 $\frac{\sqrt{6}}{4}$

查看解析
4、定义：若椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 上的两个点 $M (x_{1}, y_{1}), N (x_{2}, y_{2})$ 满足 $\frac{x_{1} x_{2}}{a^{2}} + \frac{y_{1} y_{2}}{b^{2}} = 0$ ，则称 $M, N$ 为该椭圆的一个“共轭点对”，记作 $[M, N]$ .已知椭圆 $C$ 的一个焦点坐标为 $F_{1} (- 2 \sqrt{2}, 0)$ ，且椭圆 $C$ 过点 $A (3, 1)$ .

(1)、求椭圆 $C$ 的标准方程；

(2)、求“共轭点对” $[A, B]$ 中点 $B$ 所在直线 $l$ 的方程；

(3)、设 $O$ 为坐标原点，点 $P, Q$ 在椭圆 $C$ 上，且 $P Q / / O A$ ，（2）中的直线 $l$ 与椭圆 $C$ 交于两点 $B_{1}, B_{2}$ ，且 $B_{1}$ 点的纵坐标大于0，设四点 $B_{1}, P, B_{2}, Q$ 在椭圆 $C$ 上逆时针排列.证明：四边形 $B_{1} P B_{2} Q$ 的面积小于 $8 \sqrt{3}$ .

查看解析
5、如图，在正三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，底面 $△ A B C$ 的边长为1，P为棱 $A A_{1}$ 上一点．

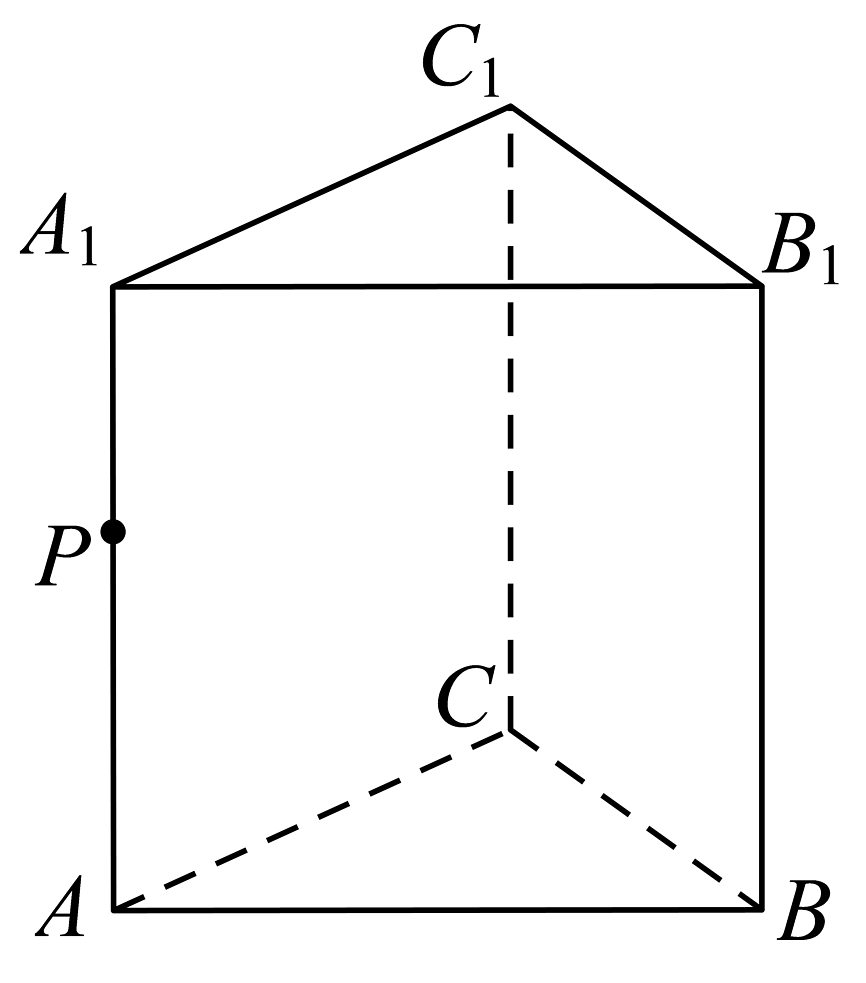(1)、若 $A A_{1} = 1$ ， P为 $A A_{1}$ 的中点，求异面直线 $P C_{1}$ 与 $A B_{1}$ 所成角的大小；

(2)、若 $A A_{1} = a (0 < a < \sqrt{3})$ ，设二面角 $A_{1} - B_{1} C_{1} - P$ 、 $A - B C - P$ 的平面角分别为 $α$ 、 $β$ ，求 $\tan (α + β)$ 的最值及取到最值时点P的位置．

查看解析
6、已知函数 $f (x) = \{\begin{array}{l} 2 x \ln x, x > 0 \\ 2 x + 1, x \leq 0 \end{array}$ ，若 $x_{1} \neq x_{2}$ 且 $f (x_{1}) = f (x_{2})$ ，则 $|x_{1} - x_{2}|$ 的最大值为．

查看解析
7、已知 $2$ 件次品和 $3$ 件正品放在一起，现需要通过检测将其区分，每次随机检测一件产品，检测后不放回，直到检测出 $2$ 件次品或者检测出 $3$ 件正品时检测结束，则恰好检测四次停止的概率为（用数字作答）．

查看解析
8、已知 $f (x) = \sin ω x \cos ω x - \sqrt{3} \cos^{2} ω x$ $(ω > 0)$ ， $x_{1}, x_{2}$ 是函数 $y = f (x) + \frac{2 + \sqrt{3}}{2}$ 的两个零点，且 ${|x_{1} - x_{2}|}_{\min} = π$ ，当 $x \in [0, \frac{7 π}{12}]$ 时， $f (x)$ 最小值与最大值之和为．

查看解析
9、设函数 $y = f (x)$ 的定义域为 $R$ ，且满足 $f (x) = f (2 - x)$ ， $f (- x) = - f (x - 2)$ ，当 $x \in [- 1, 1]$ 时， $f (x) = - x^{2} + 1$ ，则下列说法正确的是（）

A、 $f (2023) = 1$ B、当 $x \in [4, 6]$ 时， $f (x)$ 的取值范围为 $[- 1, 0]$ C、 $y = f (x + 3)$ 为奇函数 D、方程 $f (x) = lg (x + 1)$ 仅有6个不同实数解

查看解析
10、如图，设正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为 $2$ ，点 $E$ 是 $A B$ 的中点，点 $P, F$ 为空间内两点，且 $\vec{B P} = λ \vec{B C} + μ \vec{B B_{1}}, λ, μ \in [0, 1], \vec{B F} = t \vec{B C} (t \in [0, 1])$ ，则（）

A、若 $D_{1} F ⊥$ 平面 $A_{1} C_{1} D$ ，则点 $F$ 与点 $B$ 重合 B、设 $D_{1} P = \sqrt{5}$ ，则动点 $P$ 的轨迹长度为 $\frac{π}{2}$ C、平面 $C_{1} D_{1} E$ 与平面 $A_{1} D_{1} E$ 的夹角的余弦值为 $\frac{\sqrt{10}}{5}$ D、若 $t = \frac{1}{2}$ ，则平面 $D_{1} E F$ 截正方体所得截面的面积为 $\frac{7 \sqrt{17}}{6}$

查看解析
11、已知函数 $f (x) = \sin x - \frac{2}{\sin 2 x}$ ，则下列结论正确的有（）

A、 $f (x)$ 为奇函数 B、 $f (x)$ 是以 $π$ 为周期的函数 C、 $f (x)$ 的图象关于直线 $x = \frac{π}{2}$ 对称 D、 $x \in (0, \frac{π}{4}]$ 时， $f (x)$ 的最大值为 $\frac{\sqrt{2}}{2} - 2$

查看解析
12、设实数 $a > 0$ ，若不等式 $a e^{a x} - 1 ⩾ ln \frac{x}{e}$ 对任意 $x > 0$ 恒成立，则 $a$ 的最小值为（）

A、 $e$ B、 $2 e$ C、 $\frac{1}{e}$ D、 $\frac{1}{2 e}$

查看解析
13、如图，边长为2的正方形 $A B C D$ 沿对角线 $A C$ 折叠，使 $\vec{A D} \cdot \vec{B C} = 1$ ，则三棱锥 $D - A B C$ 的体积为（）

A、 $\frac{4 \sqrt{2}}{3}$ B、 $\frac{2 \sqrt{2}}{3}$ C、 $\frac{\sqrt{6}}{3}$ D、4

查看解析
14、已知双曲线 $E : \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0, b > 0)$ 的焦点关于渐近线的对称点在双曲线 $E$ 上，则双曲线 $E$ 的离心率为（）

A、2 B、 $\frac{\sqrt{5}}{12}$ C、 $\sqrt{2}$ D、 $\sqrt{5}$

查看解析
15、已知圆 $C : {(x - 3)}^{2} + {(y - 4)}^{2} = 9$ ，直线 $l : (m + 3) x - (m + 2) y + m = 0$ .则直线 $l$ 被圆 $C$ 截得的弦长的最小值为（）

A、 $2 \sqrt{7}$ B、 $\sqrt{10}$ C、 $2 \sqrt{2}$ D、 $\sqrt{6}$

查看解析
16、已知向量 $\vec{A B} = (2, 3)$ ， $\vec{A C} = (3, t)$ ，且 $\vec{A B}$ 与 $\vec{B C}$ 夹角不大于 $\frac{π}{2}$ ，则 $t$ 的取值范围为（）

A、 $(\frac{7}{3}, + \infty)$ B、 $[\frac{7}{3}, + \infty)$ C、 $(\frac{7}{3}, \frac{9}{2})$ D、 $(\frac{9}{2}, + \infty)$

查看解析
17、将函数 $f (x) = sin (ω x - \frac{π}{6}) (ω > 0)$ 的图像向右平移 $\frac{π}{2}$ 个单位长度后得到曲线 $C$ ，若 $C$ 关于 $y$ 轴对称，则 $ω$ 的最小值是（）

A、 $\frac{5}{6}$ B、 $\frac{2}{3}$ C、 $\frac{1}{3}$ D、 $\frac{1}{6}$

查看解析
18、已知复数 $z$ 满足 $(1 - i) z = 1 - 3 i$ ，则复数 $|z| =$ （）

A、 $\sqrt{3}$ B、 $\sqrt{5}$ C、 $2 \sqrt{2}$ D、 $\sqrt{10}$

查看解析
19、设全集为R ，集合 $A = \{x |3 \leq x < 6\}$ ， $B = \{x |2 < x < 9\}$ ．

(1)、分别求 $A \cap B$ ， $(∁_{R} B) \cup A$ ；

(2)、已知 $C = \{x |a < x < a + 1\}$ ，若 $C \cup B = B$ ，求实数a的取值范围．

查看解析
20、已知 $x + y = \frac{1}{x} + \frac{4}{y} + 8 (x, y > 0)$ ，则 $x + y$ 的最小值为（）

A、 $5 \sqrt{3}$ B、 $9$ C、 $4 + \sqrt{26}$ D、 $10$

查看解析

上一页 968 969 970 971 972 下一页跳转