相关试卷
-
1、“函数在区间上单调递增”的充分必要条件是( )A、 B、 C、 D、
-
2、集合 , , 则( )A、 B、 C、 D、
-
3、已知直线:与圆:相交于 , 两点,则( )A、圆心的坐标为 B、圆的半径为 C、圆心到直线的距离为2 D、
-
4、若如图中的直线的斜率分别为 , 则( )
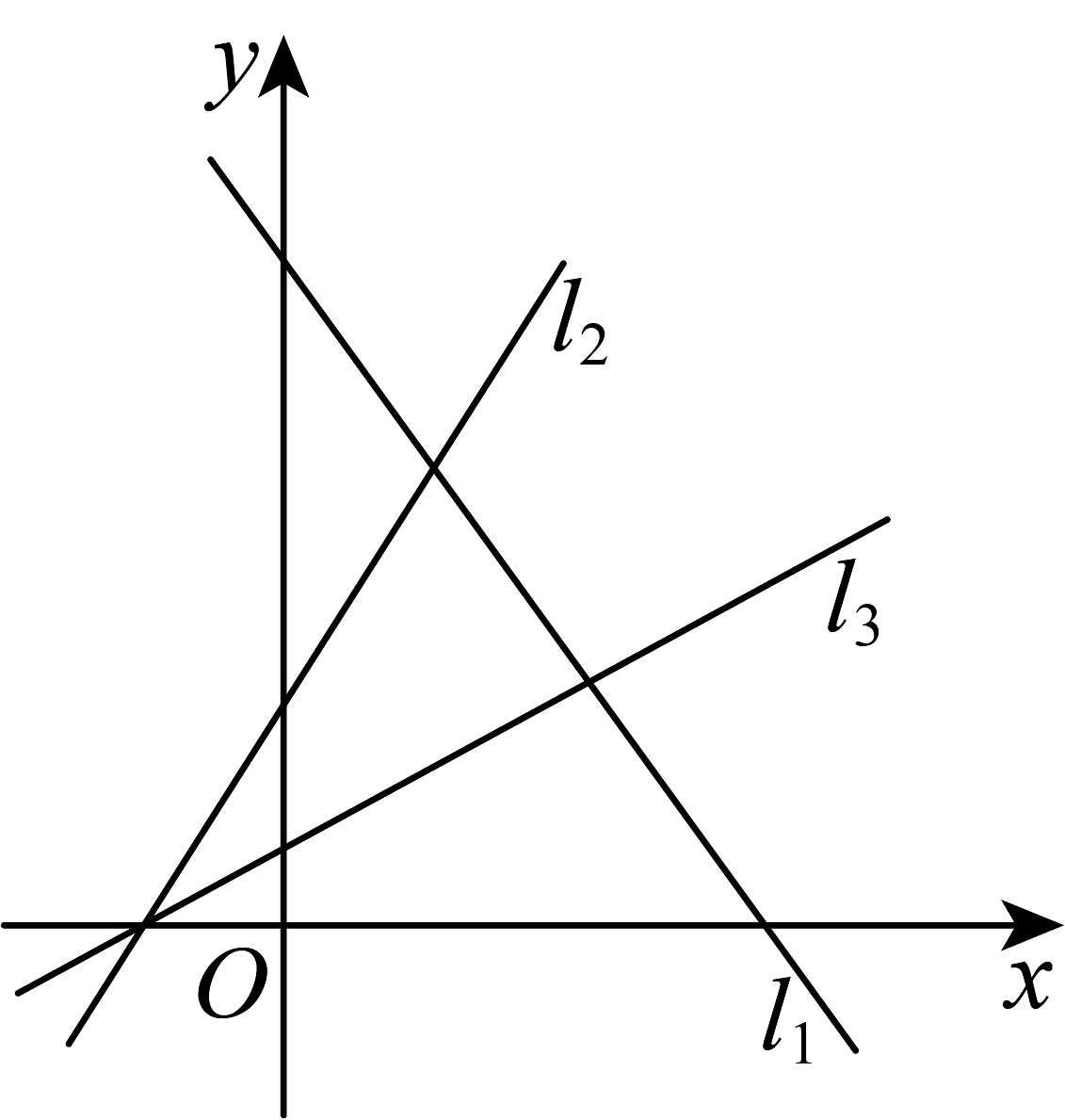 A、 B、 C、 D、
A、 B、 C、 D、 -
5、已知集合 , 实数满足.(1)、若集合 , 且 , , 是集合中最小的三个元素,求集合A;(2)、在(1)的条件下,若实数b构成的集合为B,且集合 , 若实数 , 且关于x的方程有实数解,请列出所有满足条件的有序数对.
-
6、围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元).设修建此矩形场地围墙的总费用为y.

(Ⅰ)将y表示为x的函数;
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
-
7、已知函数是定义在上的奇函数.(1)、判断函数在上的单调性,并用定义法证明你的结论;(2)、若 , 求的取值范围.
-
8、已知函数.(1)、若 , 求不等式的解集;(2)、已知 , 求不等式的解集.
-
9、已知偶函数的定义域为 , 当时,函数.(1)、求实数的值;(2)、当时,求函数的解析式;
-
10、已知函数.(1)、用分段函数的形式表示;(2)、画出的图象(请在给的平面直角坐标系中画图);(3)、求函数的值域(直接写结果).
-
11、若关于x的不等式在上恒成立,则实数a的取值范围为.
-
12、已知集合 , 集合 , 若 , 则实数m=
-
13、命题“ , ”的否定为.
-
14、下列命题中正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则
-
15、下列说法正确的是( )A、与是同一函数 B、已知 , 则 C、对于任何一个函数,如果因变量y的值不同,则自变量x的值一定不同 D、函数在其定义域内是单调递减函数
-
16、如果 , 那么函数有( )A、最大值 B、最小值 C、最大值 D、最小值
-
17、德国数学家秋利克在1837年时提出“如果对于的每一个值,总有一个完全确定的值与之对应,则是的函数,”这个定义较清楚地说明了函数的内涵,只要有一个法则,使得取值范围中的每一个值,有一个确定的和它对应就行了,不管这个对应的法则是公式、图象、表格还是其它形式.已知函数由如表给出,则的值为( )A、 B、 C、 D、
-
18、已知 , , 且 , 则的最小值为( )A、 B、 C、 D、
-
19、若函数为上的奇函数,当时, , 则的值为( )A、 B、 C、 D、
-
20、“”是“”的( )A、必要不充分条件 B、充分不必要条件 C、充要条件 D、既不充分也不必要条件