相关试卷
-
1、“直线与圆有公共点”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
2、已知函数 , 则关于的不等式的解集为( )A、 B、 C、 D、
-
3、下列四个函数中,以为其对称中心,且在区间上单调递增的是( )A、 B、 C、 D、
-
4、已知 , 是不共线的单位向量,若 , , 且 , 则( )A、 B、 C、 D、
-
5、已知全集 , , , 则图中阴影部分对应的集合为( )
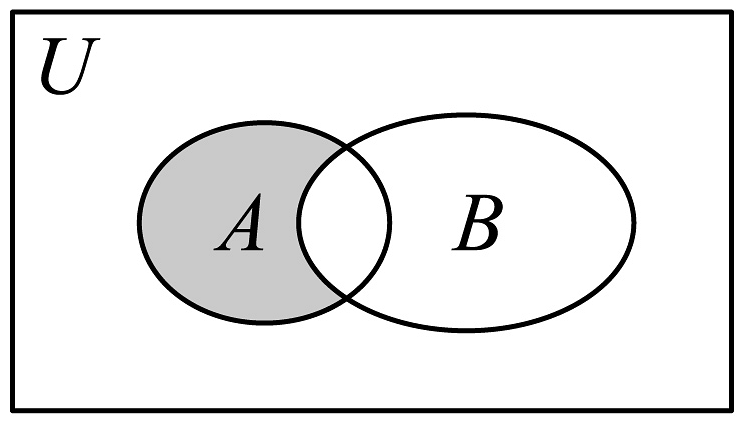 A、 B、 C、 D、
A、 B、 C、 D、 -
6、已知函数.(1)、求的图象的对称中心;(2)、当时,求的最值.
-
7、设函数 , .
(Ⅰ)已知 , 函数关于直线对称,求的值;
(Ⅱ)求函数在上的值域.
-
8、把函数的图象向左平移个单位,得到函数的图象,函数的图象关于直线对称,记函数.

(1)求函数的最小正周期和单调增区间;
(2)画出函数在区间上的大致图象.
-
9、某港口在一天之内的水深变化曲线近似满足函数 , 其中为水深(单位:米),为时间(单位:小时),该函数图象如图所示.
 (1)、求函数的解析式;(2)、若一艘货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5米的安全间隙(船底与水底的距离),则该船一天之内至多能在港口停留多久?
(1)、求函数的解析式;(2)、若一艘货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5米的安全间隙(船底与水底的距离),则该船一天之内至多能在港口停留多久? -
10、函数
(1)若方程无实根,求实数的取值范围;
(2)记的最小值为.若 , , 且 , 证明:.
-
11、已知函数的最小正周期为 .
(1)求的值;
(2)当时,求的单调区间及取值范围.
-
12、下列说法中错误的是(填序号)
①命题“ , 有”的否定是“”,有”;
②已知 , , , 则的最小值为;
③设 , 命题“若 , 则”的否命题是真命题;
④已知 , , 若命题为真命题,则的取值范围是.
-
13、已知函数 , 则( )A、的最大值为 B、直线是图象的一条对称轴 C、在区间上单调递减 D、的图象关于点对称
-
14、已知函数在处取得极小值 , 与此极小值点最近的图象的一个对称中心为 , 则下列结论正确的是( )A、 B、将的图象向左平移个单位长度即可得到的图象 C、在区间上单调递减 D、在区间上的值域为
-
15、已知 , 则下列选项一定正确的是( )A、 B、的最大值为 C、 D、
-
16、已知均为正数,则使得“”成立的充分条件可以为( )A、 B、 C、 D、
-
17、下列四个结论中正确的个数是( )
①“”是“”的充分不必要条件;
②命题:“ , ”的否定是“ , ”;
③“若 , 则”的否命题为真命题.
A、0 B、1 C、2 D、3 -
18、函数 , 和的图像都通过同一个点,则该点坐标为( )A、 B、 C、 D、
-
19、已知函数的最小正周期为 , 直线是图象的一条对称轴,则的单调递减区间为( )A、 B、 C、 D、
-
20、已知实数满足 , 则( )A、 B、 C、 D、