相关试卷
-
1、已知函数 是定义在区间 上的连续函数,若 ,使得 , ,都有 ,则称函数 是区间 上的 “ 类函数”. 下列说法正确的有( )A、函数 是区间 上的 “ 3 类函数” B、函数 是区间 上的 “ 2 类函数” C、若函数 是区间 上的 “ 类函数”,则方程 在区间 上至多只有一个解 D、若函数 是区间 上的 “ 2 类函数”,且 ,则存在满足条件的函数 ,使得
-
2、已知向量 , 则向量在上的投影向量为( )A、 B、 C、 D、
-
3、已知是第二象限角,A、 B、 C、 D、
-
4、若指数函数在上是严格增函数,则实数的取值范围是 .
-
5、如图,是以为斜边的等腰直角三角形,且. 动直线与的边共有两个公共点,即 , 在内且位于直线右侧的区域面积为.
 (1)、求的解析式;(2)、设 , 证明:是奇函数.
(1)、求的解析式;(2)、设 , 证明:是奇函数. -
6、设A是由若干个正整数组成的集合,且存在3个不同的元素 , 使得 , 则称A为“等差集”.(1)、若集合 , 且B是“等差集”,用列举法表示所有满足条件的B;(2)、若集合是“等差集”,求m的值;(3)、已知正整数 , 证明:不是“等差集”.
-
7、已知奇函数经过点.(1)、求函数的解析式;(2)、判断函数在上的单调性并用定义进行证明;(3)、若存在 , 使得不等式成立,求实数m的取值范围.
-
8、已知函数 , .(1)、若过点 , 求;(2)、若 , 当时,函数单调递增,求a的取值范围;(3)、当时,若函数图象上除原点外至少存在一对点关于原点对称,求a的范围.
-
9、(1)已知是一次函数,且满足 , 求;
(2)已知 , 求;
(3)已知函数 , 求;
-
10、已知集合.(1)、若 , 求 , ;(2)、若 , 求的取值范围.
-
11、数学学习过程中,要时刻记得这些注意点:遇到集合注意空集,遇到函数注意定义域,遇到含参方程要找定点,遇到向量要注意零向量,函数(且)的图象必过定点.
-
12、2024年10月21日,第52个梅森素数被发现,这也是迄今为止发现的最大素数.集合以这52个梅森素数为元素,其非空真子集有个.
-
13、已知函数 , 恒成立,则的取值可以为( )A、 B、2 C、5 D、8
-
14、已知函数图象经过点 , 则下列命题正确的有( )A、函数为增函数 B、函数为偶函数 C、若 , 则 D、若 , 则
-
15、已知实数a,b,c满足 , 则下列说法正确的是( )A、 B、 C、 D、
-
16、已知定义在上函数的图象是连续不断的,且满足以下条件:①;② , 当时,都有;③.则下列选项不成立的是( )A、 B、若 , 则 C、若 , 则 D、 , 使得
-
17、某食品的保鲜时间(单位:小时)与储藏温度(单位:℃)满足函数关系(…为自然对数的底数, , 为常数).若该食品在30℃的保鲜时间是18小时,在20℃的保鲜时间是36小时,则该食品在0℃的保鲜时间是( )A、54小时 B、72小时 C、108小时 D、144小时
-
18、已知函数 , 且的最大值为 , 则实数的取值范围是( )A、 B、 C、 D、
-
19、函数的图象大致是( )A、
 B、
B、 C、
C、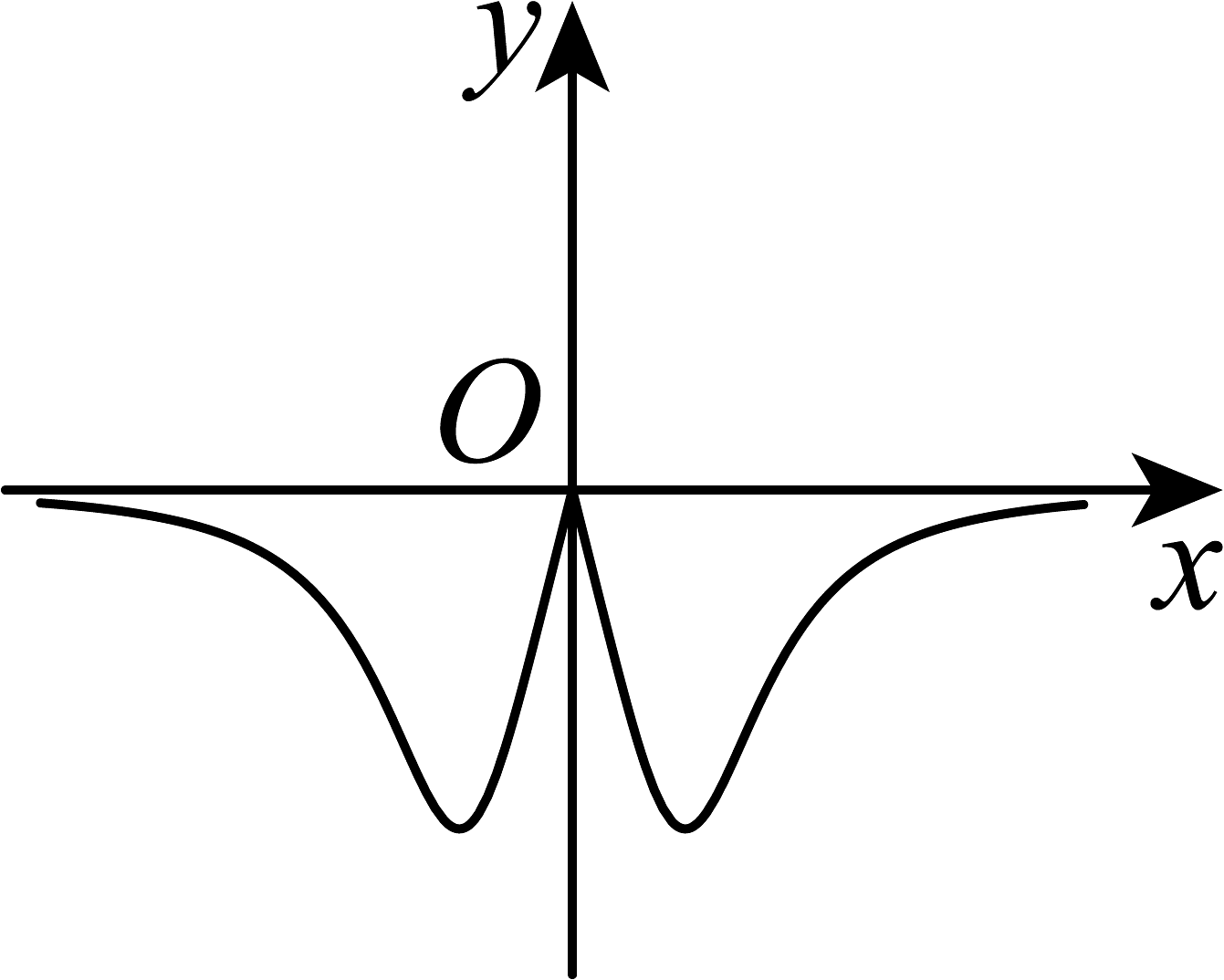 D、
D、
-
20、下列函数中,在上是增函数的是( )A、 B、 C、 D、