相关试卷
-
1、已知函数 , 将图象上所有点向左平移个单位长度得到函数的图象,若函数在区间上单调递增,则的取值范围为( )A、 B、 C、 D、
-
2、如图,计划在两个山顶间架设一条索道.为测量间的距离,施工单位测得以下数据:两个山顶的海拔高 , 在同一水平面上选一点 , 在处测得山顶的仰角分别为和 , 且测得 , 则间的距离为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
3、如图是一个古典概型的样本空间和随机事件 , 其中 , 则( )
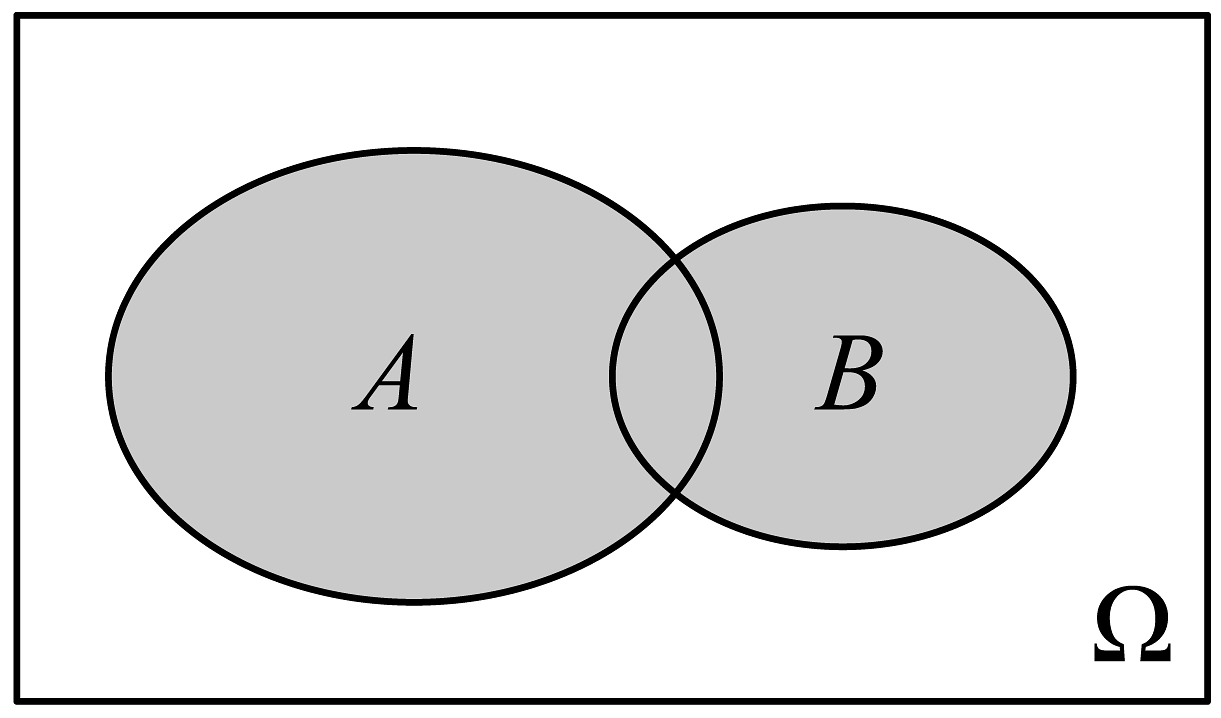 A、 B、 C、 D、
A、 B、 C、 D、 -
4、已知 , , : , : , 则是的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
5、若 , 则的虚部为( )A、 B、 C、 D、2
-
6、设集合 , 则( )A、 B、 C、 D、
-
7、中,为边的中点,.
 (1)、若的面积为 , 且 , 求的值;(2)、若 , 求的取值范围.
(1)、若的面积为 , 且 , 求的值;(2)、若 , 求的取值范围. -
8、已知函数(1)、写出函数的单调递减区间;(2)、设 , 求的最值.
-
9、已知向量是同一平面内的三个向量,其中 .(1)、若 , 且 , 求向量的坐标;(2)、若是单位向量,且 , 求与的夹角.(3)、若 , 求向量在向量上的投影向量(用坐标表示).
-
10、如图,在四棱锥中,已知底面为平行四边形,点为棱的中点.

(1)求证:平面;
(2)设平面平面 , 点在上,求证:为的中点.
-
11、如图,正方体的棱长为1,为的中点,为线段上的动点,过点 , , 的平面截该正方体所得截面记为 , 则下列命题正确的是 (写出所有正确命题的编号)

①当时,为等腰梯形.
②当时,与的交点满足.
③当时,为四边形.
④当时,的面积为.
-
12、在中,若 , 则
-
13、已知以为起点的向量 , 在正方形网格中的位置如图所示、网格纸上小正方形的边长为1,则.

-
14、在三角形所在平面内,点满足 , 其中 , , , , 则下列说法正确的是( )A、当时,直线一定经过三角形的重心 B、当时,直线一定经过三角形的外心 C、当时,直线一定经过三角形的垂心 D、当时,直线一定经过三角形的内心
-
15、下列命题中正确的是( )A、用与球心距离为1的平面去截球,所得截面圆的面积为 , 则球的表面积为 B、圆柱形容器底半径为 , 两直径为的玻璃球都浸没在容器的水中,若取出这两个小球,则容器内水面下降的高度为 C、正四棱台的上下底面边长分别为2,4,侧棱长为2,其体积为 D、已知圆锥的母线长为10,侧面展开图的圆心角为 , 则该圆锥的体积为
-
16、已知向量 , , 满足 , , 则下列结论正确的是( )A、 B、与的夹角为 C、 D、在上的投影向量为
-
17、已知正六边形ABCDEF的边长为2,圆O的圆心为正六边形的中心,半径为1,若点P在正六边形的边上运动,MN为圆O的直径,则的取值范围是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
18、一艘游轮航行到处时看灯塔在的北偏东 , 距离为海里,灯塔在的北偏西 , 距离为海里,该游轮由沿正北方向继续航行到处时再看灯塔在其南偏东方向,则此时灯塔位于游轮的( )A、正西方向 B、南偏西方向 C、南偏西方向 D、南偏西方向
-
19、中,分别是角的对边,且 , 则的形状为( )A、直角三角形 B、钝角三角形 C、直角或钝角三角形 D、锐角三角形
-
20、在平面直角坐标系中,已知双曲线的右焦点为 , 一条渐近线的倾斜角为 , 点在双曲线上.(1)、求双曲线的标准方程;(2)、若点在直线上,点在双曲线上,且焦点在以线段为直径的圆上,分别记直线的斜率为 , 求的值.