相关试卷
-
1、设函数(1)、当时,求曲线在处的切线方程.(2)、讨论函数在区间上零点的个数.
-
2、已知函数若在区间上存在个不同的数 , , , …, , 使得成立,则的最大值为 .
-
3、工人在悬挂如图所示的一个正六边形装饰品时,需要固定六个位置上的螺丝,首先随意拧紧一个螺丝,接着拧紧距离它最远的第二个螺丝,再随意拧紧第三个螺丝,接着拧紧距离第三个螺丝最远的第四个螺丝,第五个和第六个以此类推,则不同的固定方式有种.

-
4、已知函数(n为正整数),则下列判断正确的是( )A、函数始终为奇函数 B、当n为偶数时,函数的最小值为4 C、当n为奇数时,函数的极小值为4 D、当时,函数的图象关于直线对称
-
5、下列等式中,正确的是( )A、 B、 C、 D、
-
6、已知函数 , 若函数在内有且仅有两个零点,则实数的取值范围是( )A、 B、 C、 D、
-
7、设是函数的导数,是的导数,若方程有实数解 , 则称点为函数的“拐点”.已知:任何三次函数既有拐点,又有对称中心,且拐点就是对称中心.设 , 数列的通项公式为 , 则( )A、5 B、6 C、7 D、8
-
8、2010年广州亚运会结束了,某运动队的7名队员合影留念,计划站成一横排,但甲不站最左端,乙不站最右端,丙不站正中间.则理论上他们的排法有( )A、3864种 B、3216种 C、3144种 D、2952种
-
9、设是偶函数(且)的导函数, , 当时, , 则使成立的的取值范围是( )A、 B、 C、 D、
-
10、若曲线在点处的切线在y轴上的截距为1,则( )A、 B、0 C、1 D、2
-
11、函数的图象不可能是( )A、
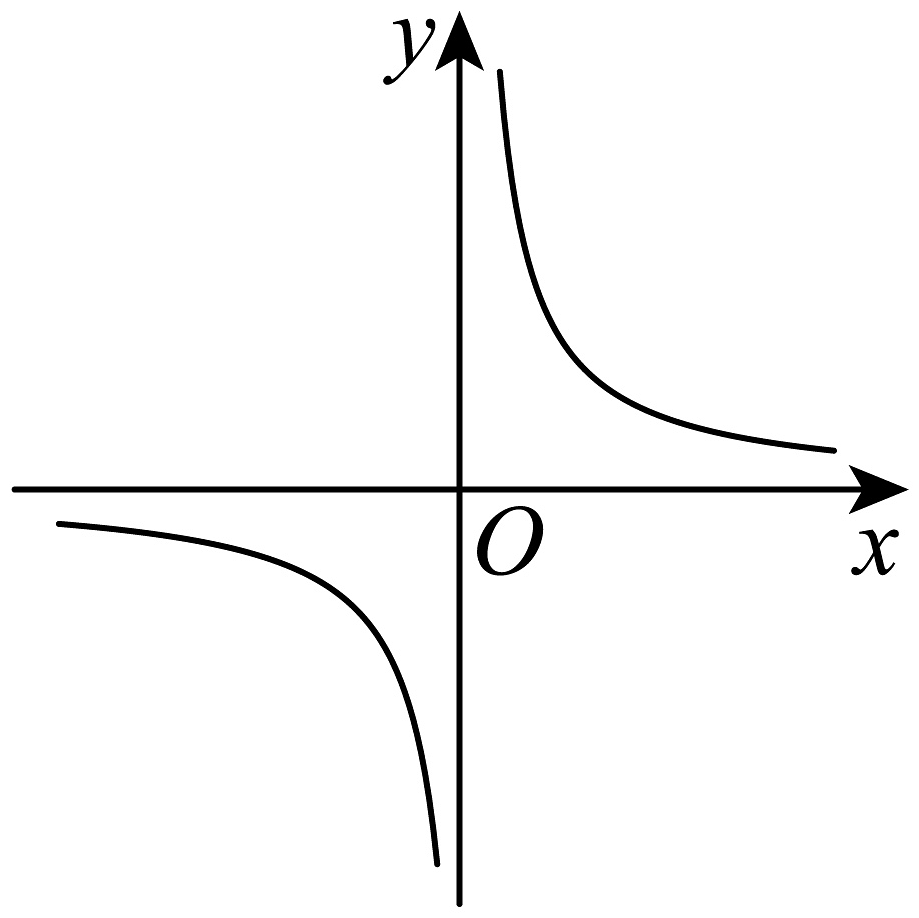 B、
B、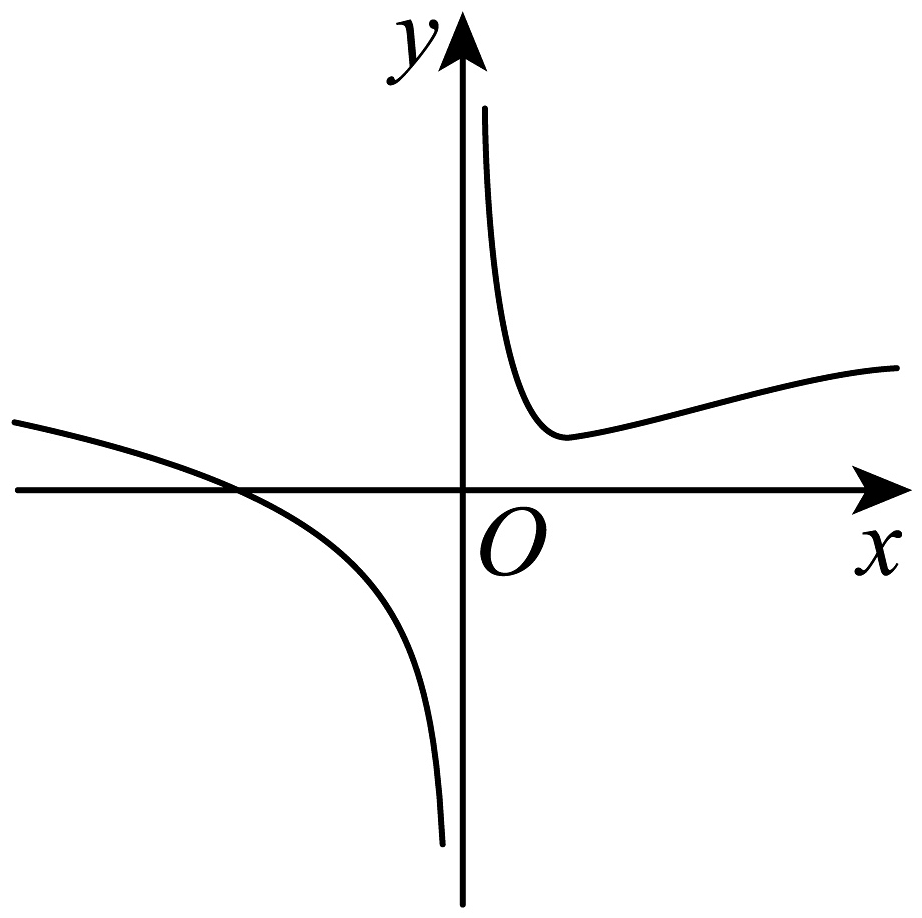 C、
C、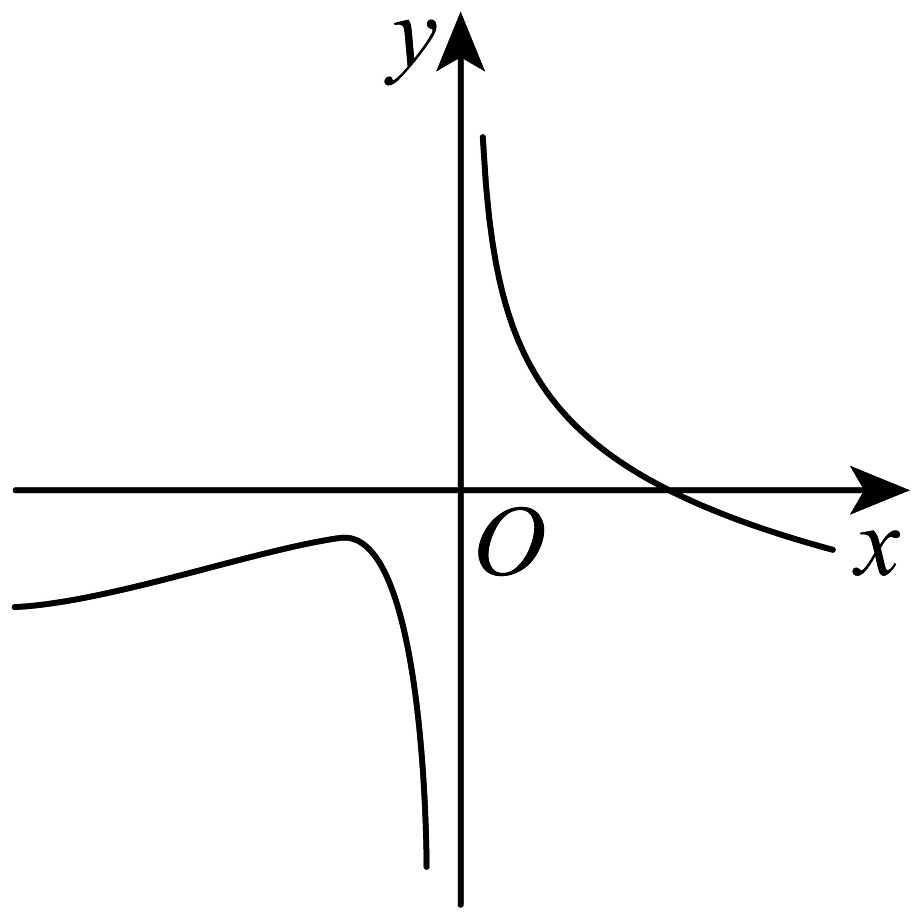 D、
D、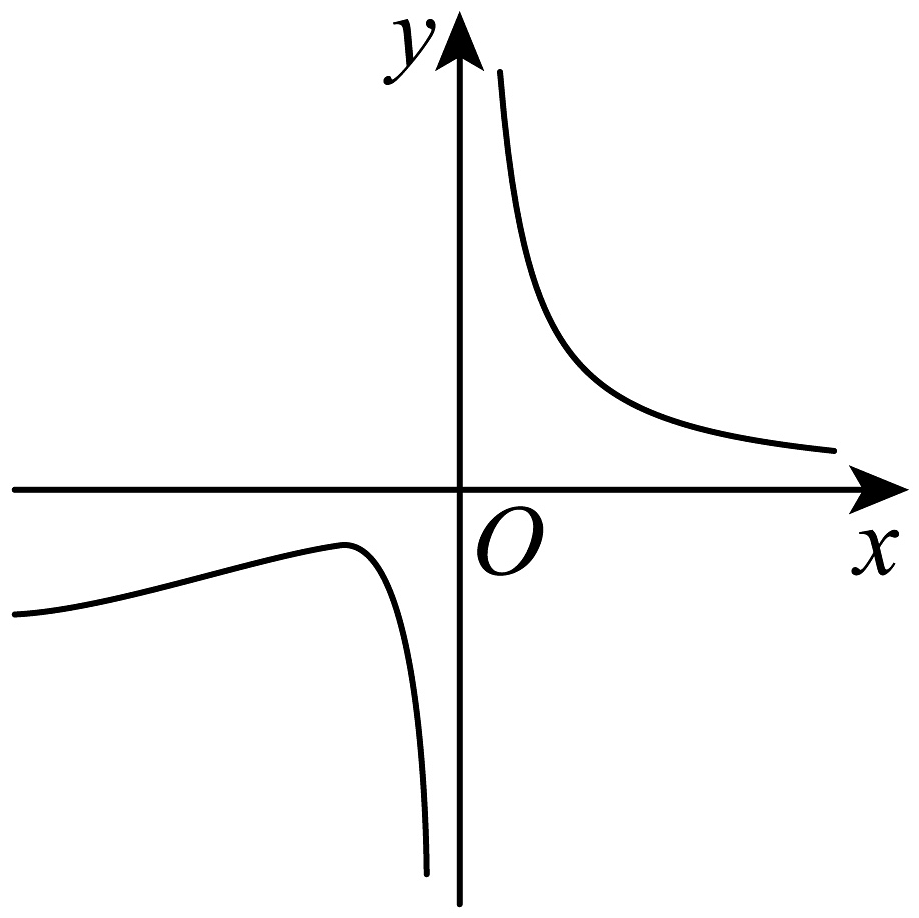
-
12、对于函数 , , 如果存在实数 , , 使得 , 那么称函数为的“重组函数”(1)、已知 , , 是否存在实数 , , 使得是的重组函数?若存在,求出 , , ;若不存在,试说明理由.(2)、当 , 时,求的重组函数的值域.(3)、当 , 时,的重组函数有唯一的零点,求实数的取值范围.
-
13、已知函数 .(1)、求的最小正周期;(2)、若是锐角,且 , 求角的正弦值;(3)、在锐角中,角 , , 所对的边分别为 , , , 若 , , 求周长的取值范围.
-
14、某广场设置了一些石凳供大家休息,这些石凳是由棱长为的正四面体沿棱的三等分点,截去四个一样的正四面体得到.
 (1)、求石凳的体积与原正四面体的体积之比;(2)、为了美观工人准备将石凳的表面进行粉刷,已知每平方米造价50元,请问粉刷一个石凳需要多少钱?()
(1)、求石凳的体积与原正四面体的体积之比;(2)、为了美观工人准备将石凳的表面进行粉刷,已知每平方米造价50元,请问粉刷一个石凳需要多少钱?() -
15、在中,角 , , 的对边分别是 , , 且 .(1)、求角的大小;(2)、若 , 为的中点, , 求.
-
16、已知 .(1)、求;(2)、当为何值时,与垂直?
-
17、已知在中,角的对边分别为 , , 为的内心,为与同向的单位向量,则在上的投影向量为(用表示)
-
18、圆锥的侧面展开图是半径为的半圆,则该圆锥的体积为.
-
19、角的终边上有一点 , 则
-
20、如图,已知正方体的棱长为 , , , 分别是棱 , , 的中点,则下列说法正确的是( )
 A、与是共面直线 B、如果正方体的所有顶点在一个球面上,则这个球的体积为 C、过 , , 三点作一个截面,截得的几何体的体积 D、若在上存在一点使得最小,最小值为
A、与是共面直线 B、如果正方体的所有顶点在一个球面上,则这个球的体积为 C、过 , , 三点作一个截面,截得的几何体的体积 D、若在上存在一点使得最小,最小值为