相关试卷
-
1、定义在上的函数满足以下条件:① , ②对任意 , 当时都有 , 则 , , 的大小关系是( )A、 B、 C、 D、
-
2、下列图形中,可以表示函数的是( )A、
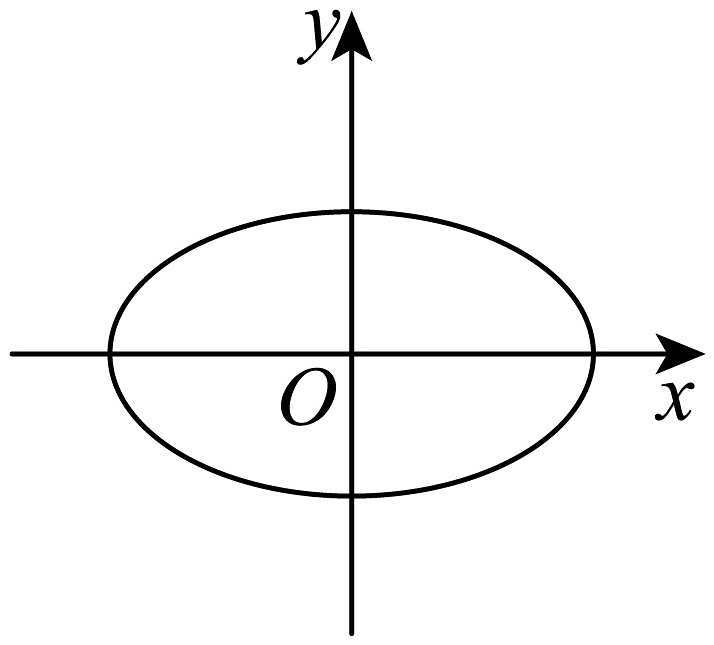 B、
B、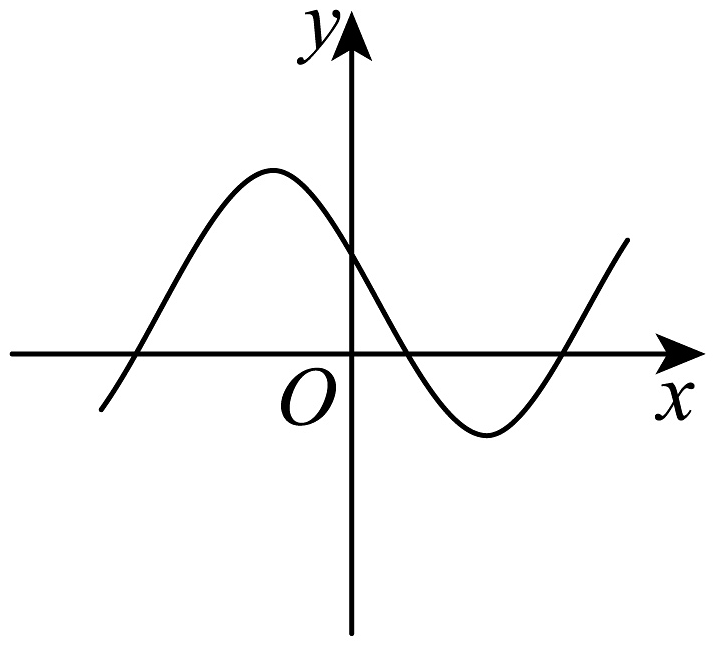 C、
C、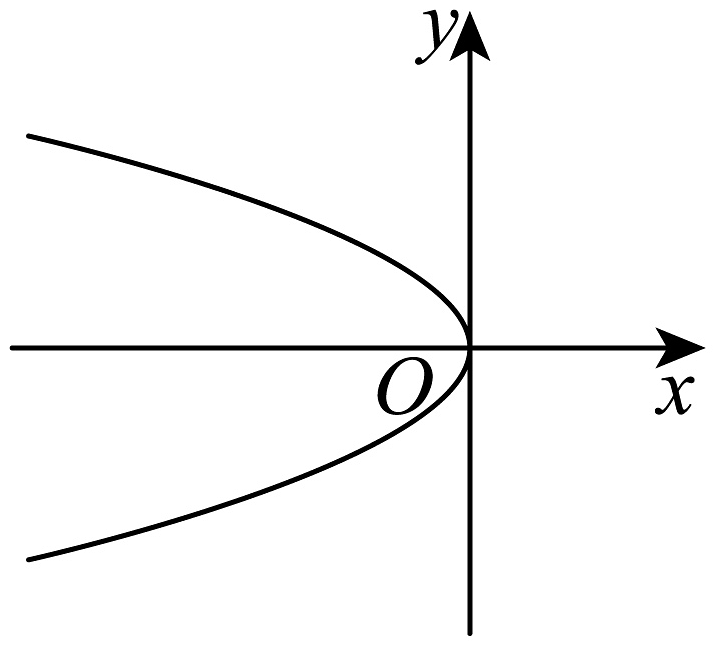 D、
D、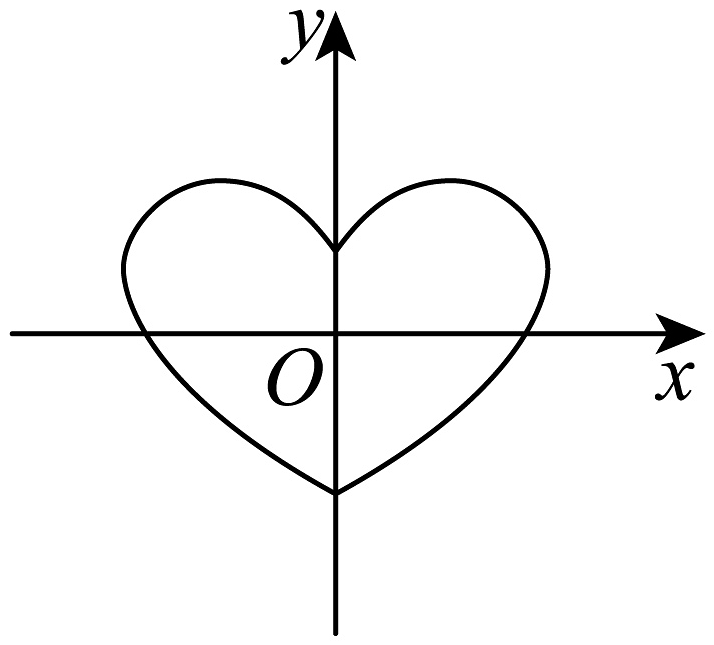
-
3、已知三棱柱 , 底面三角形为正三角形,侧棱底面 , , 为的中点,为中点.

(1)求证:直线平面;
(2)求平面和平面所成的锐二面角的余弦值.
-
4、设函数 .(1)、求函数F(x)的单调区间.(2)、若方程有且仅有三个实根,求实数的取值范围.
-
5、抛物线的焦点为F,过F的直线与抛物线交于A、B两点,且满足 , 点O为原点,则的面积为.
-
6、已知定义在R上的函数满足 , 则下列式子成立的是( )A、 B、 C、是R上的增函数 D、 , 则有
-
7、【2018江西抚州市高三八校联考】已知双曲线 ( , )与抛物线有相同的焦点 , 且双曲线的一条渐近线与抛物线的准线交于点 , 则双曲线的离心率为( )A、 B、 C、 D、
-
8、已知、是椭圆上关于原点对称的两点,是椭圆上任意一点,且直线、的斜率分别为、(),若的最小值为 , 则椭圆的离心率为( ).A、 B、 C、 D、
-
9、在数列中, , 其前n项和为 , 且(且).(1)、求的通项公式;(2)、设数列满足 , 其前项和为 , 若恒成立,求实数的取值范围.
-
10、下列命题正确的是( )A、命题“ , ”的否定是“ , ” B、与是同一个函数 C、函数的值域为 D、若函数的定义域为 , 则函数的定义域为
-
11、已知函数和的定义域分别为和 , 若对任意 , 恰好存在个不同的实数 , 使得(其中),则称为的“重覆盖函数”.(1)、试判断是否为的“2重覆盖函数”?请说明理由;(2)、若 , 为 , 的“2重覆盖函数”,求实数的取值范围;(3)、函数表示不超过的最大整数,如 . 若为的“2024重覆盖函数”,求正实数的取值范围.
-
12、如图,在正方体中,为的中点.
 (1)、求证:平面;(2)、连接交于点 , 求三棱锥的体积;(3)、已知点为中点,点为平面内的一个动点,若平面 , 求长度的最小值.
(1)、求证:平面;(2)、连接交于点 , 求三棱锥的体积;(3)、已知点为中点,点为平面内的一个动点,若平面 , 求长度的最小值. -
13、如图,在菱形中,分别是边的中点,与交于点 , 设 .
 (1)、用表示;(2)、求的余弦值.
(1)、用表示;(2)、求的余弦值. -
14、已知函数的最小正周期为 .(1)、求的值;(2)、求在上的值域.
-
15、球面被平面所截得的一部分叫做球冠,截得的圆叫做球冠的底,垂直于截面的直径被截得的一段叫做球冠的高球体被平面截下的一部分几何体叫做球缺,截面叫做球缺的底面,垂直于截面的直径被截下的线段长叫做球缺的高,球缺是旋转体,可以看做是球冠和其底所在的圆面所围成的几何体.如图1,一个球面的半径为 , 球冠的高是 , 球冠的表面积公式是 , 与之对应的球缺的体积公式是 . 如图2,已知是以为直径的圆上的两点, , 则扇形绕直线旋转一周形成的几何体的表面积为 , 体积为 .

-
16、勒洛三角形是一种典型的定宽曲线,以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形就是勒洛三角形.在如图所示的勒洛三角形中,已知为弧(含端点)上的一点,则的范围为 .

-
17、已知函数 , 则 .
-
18、函数的部分图象如图所示,则下列说法中正确的是( )
 A、 B、的表达式可以写成 C、的图象向左平移个单位长度后得到的新函数是偶函数 D、若方程在上有且只有6个根,则
A、 B、的表达式可以写成 C、的图象向左平移个单位长度后得到的新函数是偶函数 D、若方程在上有且只有6个根,则 -
19、已知 , 为两个不同的平面, , 为两条不同的直线,A为点,下列说法不正确的是( )A、 B、为异面直线 C、 D、
-
20、在中,内角的对边分别为 , 且 , 则的最大值为( )A、2 B、4 C、 D、