相关试卷
-
1、已知定义在上的可导函数f(x)的导函数为f(x),满足且为偶函数.为奇函数,若 , 则不等式的解集为( )A、 B、 C、 D、
-
2、已知 , 若 , 则.
-
3、已知双曲线的左、右焦点分别为 , , 双曲线上一点A关于原点O对称的点为B,且满足 , , 则该双曲线的渐近线方程为 .
-
4、函数的最大值为.
-
5、若圆关于直线对称,则 .
-
6、已知 , 则( )A、 B、 C、 D、2
-
7、椭圆的长轴长为6,则该椭圆的离心率为( )A、 B、 C、 D、
-
8、已知 , 且 , 则的最小值为( )A、4 B、 C、6 D、8
-
9、5个人排成一排,如果甲必须站在排头或排尾,而乙不能站在排头或排尾,那么不同站法总数为( )A、18 B、36 C、48 D、60
-
10、已知等差数列的首项为1,若成等比数列,则( )A、-2 B、4 C、8 D、-2或4
-
11、已知 , 为虚数单位,若复数的实部与虚部相等,则( )A、 B、 C、 D、
-
12、已知平面向量 , 若 , 则( )A、 B、 C、2 D、
-
13、下列选项正确的是( )A、 B、 C、 D、
-
14、如图,正方体的棱长为1,E是的中点,则( )
 A、直线平面 B、 C、三棱锥的体积为 D、三棱锥的外接球的表面积为
A、直线平面 B、 C、三棱锥的体积为 D、三棱锥的外接球的表面积为 -
15、折纸又称“工艺折纸”,是一种把纸张折成各种不同形状物品的艺术活动,在我国源远流长.某些折纸活动蕴含丰富的数学内容,例如:如图,用圆形纸片,按如下步骤折纸.
步骤1:设圆心是 , 在圆内不是圆心处取一点,标记为;
步骤2:把纸片对折,使圆周正好通过点 , 此时圆周上与点重合的点标记为;
步骤3:把纸片展开,于是就留下一条折痕,此时与折痕交于点;
步骤4:不断重复步骤2和3,能得到越来越多条折痕和越来越多的交点 .
现取半径为4的圆形纸片,定点到圆心的距离为2,按上述方法折纸.以线段的中点为原点,线段所在直线为轴,建立平面直角坐标系 , 记动点的轨迹为曲线 .
 (1)、求曲线的标准方程;(2)、已知点 , 点A,B是曲线上两个不同的动点(不在轴上),直线的斜率分别为 , 且 , 证明:直线过定点.
(1)、求曲线的标准方程;(2)、已知点 , 点A,B是曲线上两个不同的动点(不在轴上),直线的斜率分别为 , 且 , 证明:直线过定点. -
16、已知函数 , 则下列说法正确的是( )A、当时,在上是增函数 B、当时,在处的切线与坐标轴围成的三角形的面积为 C、若在上为减函数,则 D、当时,若函数有且只有一个零点,则
-
17、已知点是离心率为的椭圆:上的一点.(1)、求椭圆的方程;(2)、点在椭圆上,点关于坐标原点的对称点为 , 直线和的斜率都存在且不为 , 试问直线和的斜率之积是否为定值?若是,求此定值;若不是,请说明理由;(3)、斜率为的直线交椭圆于、两点,求面积的最大值,并求此时直线的方程.
-
18、如图,在四棱锥中,平面 , 底面是直角梯形,其中 , , , , 为棱上的点,且 , 点在棱上(不与点 , 重合).
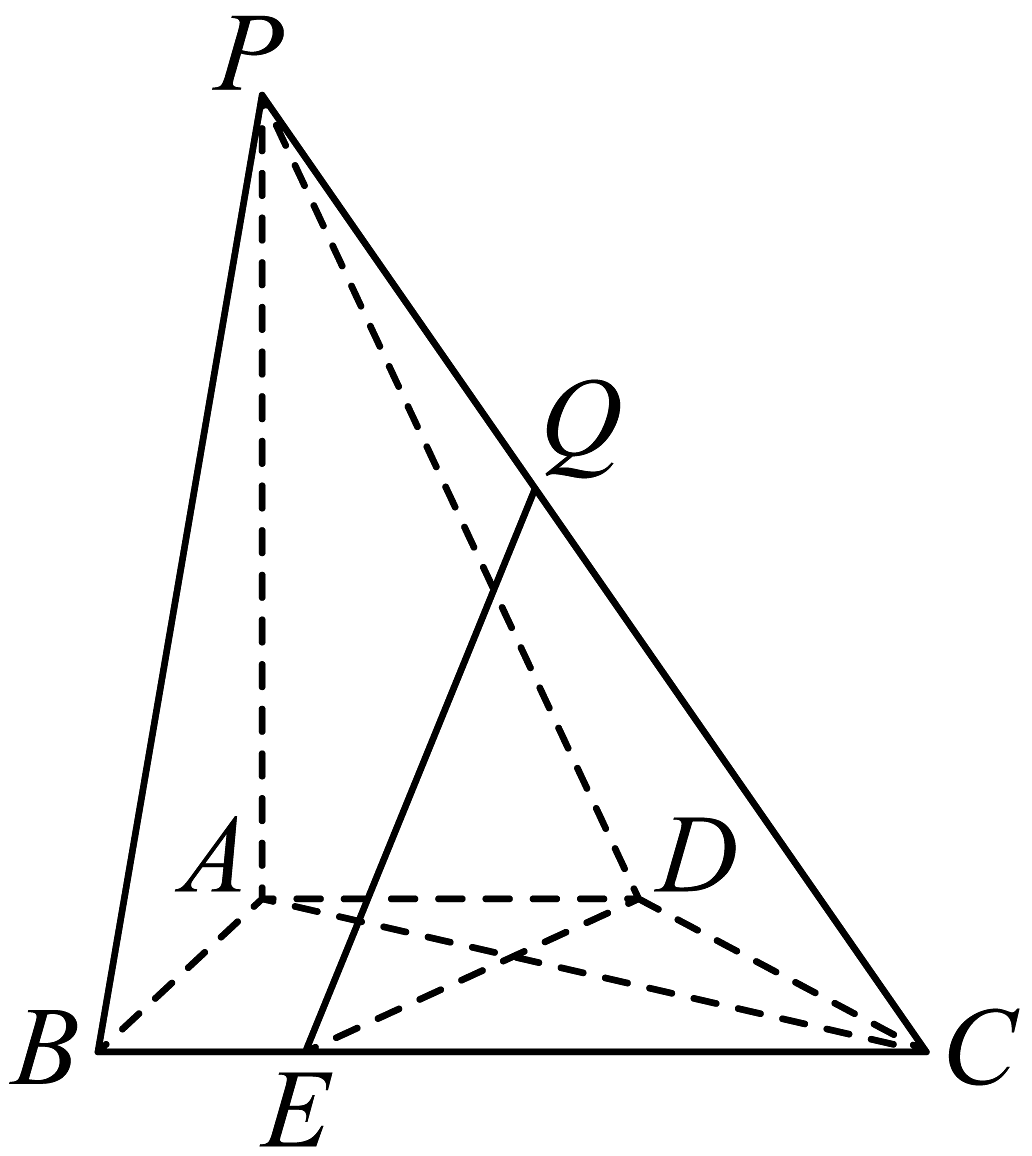 (1)、求证:平面平面;(2)、求二面角的平面角的余弦值;(3)、直线能与平面垂直吗?若能,求出的值;若不能,请说明理由.
(1)、求证:平面平面;(2)、求二面角的平面角的余弦值;(3)、直线能与平面垂直吗?若能,求出的值;若不能,请说明理由. -
19、设平面内两个非零向量的夹角为 , 定义一种运算“”: . 试求解下列问题:(1)、已知向量满足 , 求的值;(2)、①若 , 用坐标表示;
②在平面直角坐标系中,已知点 , 求的值;
(3)、已知向量 , 求的最小值. -
20、如图,某公园有一块扇形人工湖OMN,其中圆心角 , 半径为1千米,为了增加观赏性,公园在人工湖中划分出一片荷花池,荷花池的形状为矩形(四个顶点都落在扇形边界上);再建造一个观景台,形状为 , 记
 (1)、当角取何值时,荷花池的面积最大?并求出最大面积.(2)、若在OA的位置架起一座观景桥,已知建造观景桥的费用为每千米8万元不计桥的宽度;且建造观景台的费用为每平方千米16万元,求建造总费用的范围.
(1)、当角取何值时,荷花池的面积最大?并求出最大面积.(2)、若在OA的位置架起一座观景桥,已知建造观景桥的费用为每千米8万元不计桥的宽度;且建造观景台的费用为每平方千米16万元,求建造总费用的范围.