版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、若数列 $\{a_{n}\}$ 满足 $a_{n + 1} = S_{n} + 1$ ， $a_{1} = 0$ ，则 $a_{8} =$ .

查看解析
2、有3台车床加工同一型号的零件. 第1台加工的次品率为 $6 %$ ，第2，3台加工的次品率均为 $5 %$ ，加工出来的零件混放在一起. 已知第1，2，3台车床的零件数分别占总数的 $25 %$ ， $30 %$ ， $45 %$ . 则下列结论正确的是（）

A、任取一个零件，它是第1台车床加工的次品的概率为 $0.06$ B、任取一个零件，它是次品的概率为 $0.0525$ C、如果取到的零件是次品，它是第2台车床加工的概率为 $\frac{2}{7}$ D、如果取到的零件不是第3台车床加工的，它是次品的概率为 $\frac{3}{55}$

查看解析
3、如图，正方形 $A B C D$ 的边长为 $2 cm$ ，取正方形 $A B C D$ 各边的中点 $E$ ， $F$ ， $G$ ， $H$ ，作第2个正方形 $E F G H$ ，然后再取正方形 $E F G H$ 各边的中点 $I$ ， $J$ ， $K$ ， $L$ ，作第3个正方形的 $I J K L$ ，依此方法一直继续下去. 设第 $k$ 个正方形面积为 $a_{k}$ ，则下列结论正确的是（）

A、 $a_{3} = 1 {cm}^{2}$ B、 $a_{2} = 16 a_{6}$ C、前6个正方形面积和为 $\frac{63}{16} {cm}^{2}$ D、如果这个作图过程可以一直继续下去，那么这些正方形的面积之和将趋近 $8 {cm}^{2}$

查看解析
4、设离散型随机变量 $X$ 的分布列如下表，若离散型随机变量 $Y$ 满足 $Y = 2 X - 1$ . 则下列结论正确的是（）
$X$
0
1
2
3
$P$
$q$
0.2
0.1
0.2

A、 $E (X) = 1.2$ B、 $E (Y) = 1$ C、 $D (X) = 1.4$ D、 $D (Y) = 28$

查看解析
5、有一个游戏，规则如下：如图，在圆上有 $A$ ， $B$ ， $C$ ， $D$ ， $E$ ， $F$ ， $G$ ， $H$ 共八个点，一枚棋子起始位置在点 $A$ 处，抛掷一枚均匀的骰子，若骰子正面向上的点数为 $i (i = 1, 2, \dots, 6)$ . 则棋子前进 $i$ 步，每步从一个点按顺时针方向前进到相邻的另一个点，可以循环进行，抛掷三次骰子后，游戏结束.若此时棋子在点 $A$ 处，则游戏过关. 试问游戏结束时过关的概率为（）

A、 $\frac{1}{18}$ B、 $\frac{1}{12}$ C、 $\frac{1}{6}$ D、 $\frac{1}{8}$

查看解析
6、下列四个不等式① $ln x < x < e^{x}$ ， ② $e^{x - 1} \geq x$ ， ③ $ln x \geq x - 1$ ， ④ $x ln x \geq x - 1$ 中正确的个数为（）

A、1 B、2 C、3 D、4

查看解析
7、某企业节能降耗技术改造后，在生产某产品过程中的产量 $x$ （吨）与相应的生产能耗 $y$ （吨）的几组对应数据如表所示：
$x$
3
4
5
6
$y$
2.5
3
4
4.5
根据表中数据得出 $y$ 关于 $x$ 的线性回归方程为 $y = 0.7 x + \hat{a}$ ，若生产7吨产品，预计相应的生产能耗为（）

A、5.15吨 B、5.25吨 C、5.5吨 D、9.5吨

查看解析
8、2025有（）个不同的正因数

A、8 B、10 C、12 D、15

查看解析
9、五一假期期间，某单位安排5人值5天班，每人值班一天，要求甲不值第一天，乙不值第五天，则不同安排方法的种数有（）

A、42 B、72 C、78 D、96

查看解析
10、已知函数 $f (x) = x - ln x$ ，则 $f (x)$ 单调递增区间是（）

A、 $(- \infty, 0)$ B、 $(1, + \infty)$ C、 $(- \infty, 0) \cup (1, + \infty)$ D、 $(0, 1)$

查看解析
11、已知随机变量 $ξ$ 服从正态分布 $N (3, σ^{2})$ ，且 $P (ξ < 4) = 0.6$ ，则 $P (ξ < 2)$ 等于（）

A、0.1 B、0.2 C、0.3 D、0.4

查看解析
12、在等差数列 $\{a_{n}\}$ 中， $S_{n}$ 为其前 $n$ 项和，若 $S_{3} = 1$ ， $S_{6} = 4$ ，则 $S_{9} =$ （）

A、7 B、8 C、9 D、12

查看解析
13、在 $△ A B C$ 中，角A，B，C所对的边分别为a，b，c， $2 a - c = 2 b cos C$ .

(1)、求B；

(2)、若点D为边BC的中点，点E，F分别在边AB，AC（包括顶点）上， $∠ E D F = \frac{π}{6}$ ， $b = c = 2$ .设 $∠ B D E = α$ ，将 $△ D E F$ 的面积S表示为 $α$ 的函数，并求S的取值范围.

查看解析
14、某学校为了解本校历史、物理方向学生的学业水平模拟测试数学成绩情况，分别从物理方向的学生中随机抽取60人的成绩得到样本甲，从历史方向的学生中随机抽取n人的成绩得到样本乙，根据两个样本数据分别得到如下直方图：
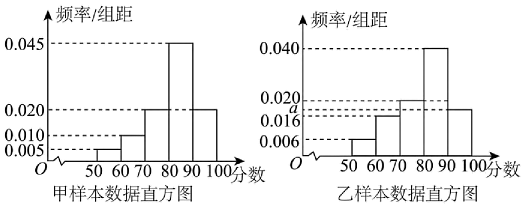
已知乙样本中数据在 $[70, 80)$ 的有10个．

(1)、求n和乙样本直方图中a的值；

(2)、试估计该校物理方向的学生本次模拟测试数学成绩的平均值和历史方向的学生本次模拟测试数学成绩的第75百位数（同一组中的数据用该组区间中点值为代表）；

(3)、采用分层抽样的方法从甲样本数据中分数在 $[60, 70)$ 和 $[70, 80)$ 的学生中抽取6人，并从这6人中任取2人，求这两人分数都在 $[70, 80)$ 中的概率．

查看解析
15、 $G$ 是 $△ A B C$ 的重心， $A B = 2, A C = 4, ∠ C A B = 120^{\circ}, P$ 是 $△ A B C$ 所在平面内的一点，则下列结论正确的是（）

A、 $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ B、 $\vec{A B}$ 在 $\vec{A C}$ 上的投影向量等于 $- \frac{1}{2} \vec{A C}$ . C、 $|\vec{A G}| = \frac{2 \sqrt{3}}{3}$ D、 $\vec{A P} \cdot (\vec{B P} + \vec{C P})$ 的最小值为 $- \frac{3}{2}$

查看解析
16、已知函数 $f (x)$ 和 $g (x)$ 的定义域分别为 $D_{1}$ 和 $D_{2}$ ，若对任意 $x_{0} \in D_{1}$ ，恰好存在n个不同的实数 $x_{1}$ ， $x_{2}$ ， …， $x_{n} \in D_{2}$ ，使得 $g (x_{i}) = f (x_{0})$ （其中 $i = 1$ ， 2，…，n， $n \in N^{*}$ ），则称 $g (x)$ 为 $f (x)$ 的“n重覆盖函数”.

(1)、判断 $g (x) = x^{2} - 2 x + 1$ （ $x \in [0, 4]$ ）是否为 $f (x) = x + 4$ （ $x \in [0, 5]$ ）的“n重覆盖函数”，如果是，求出n的值；如果不是，说明理由；

(2)、若 $g (x) = \{\begin{array}{l} a x^{2} + (2 a - 3) x + 1, - 2 \leq x \leq 1 \\ x - 1, x > 1 \end{array}$ 为 $f (x) = \log_{2} \frac{2^{x} + 2}{2^{x} + 1}$ 的“2重覆盖函数”，求实数a的取值范围；

(3)、函数 $[x]$ 表示不超过x的最大整数，如 $[1.2] = 1$ ， $[2] = 2$ ， $[- 1.2] = - 2$ ，若 $h (x) = a x - [a x]$ ， $x \in [0, 2)$ 为 $f (x) = \frac{x}{x^{2} + 1}$ ， $x \in [0, + \infty)$ 的“2024重覆盖函数”，求正实数a的取值范围.

查看解析
17、在 $△ A B C$ 中，角 $A, B, C$ 所对的边分别为 $a, b, c$ ， $2 c \sin A \cos B + b \sin B = \frac{5}{2} c \sin A$

(1)、求 $\frac{\sin A}{\sin C}$

(2)、若 $a > c$ ，角 $B$ 的平分线交 $A C$ 于 $D$ .
（I）求证： $B D^{2} = B A \cdot B C - D A \cdot D C$ .
（II）若 $a = 1$ ，求 $D B \cdot A C$ 的最大值

查看解析
18、如图，四棱锥 $P - A B C D$ 中， $P A ⊥$ 平面ABCD，PB与底面所成的角为 $45^{\circ}$ ，底面ABCD为直角梯形， $∠ A B C = ∠ B A D = 90^{\circ} ， A D = 2 P A = 2 B C = 2$

(1)、求证：平面 $P A C ⊥$ 平面PCD：

(2)、在线段PD上是否存在点E，使CE与平面PAD所成的角为 $45^{\circ}$ ？若存在，求出有 $\frac{P E}{P D}$ 的值：若不存在，说明理由.

查看解析
19、某市为提高市民对文明城市创建的认识，举办了“创建文明城市”知识竞赛，从所有答卷中随机抽取100份作为样本，将样本的成绩（满分100分，成绩均为不低于40分的整数）分成六段： $[40, 50)$ ， $[50, 60)$ ， $\dots$ ， $[90, 100]$ 得到如图所示的频率分布直方图.

(1)、求频率分布直方图中 $a$ 的值；

(2)、求样本成绩的第75百分位数；

(3)、已知落在 $[50, 60)$ 的平均成绩是56，方差是7，落在 $[60, 70)$ 的平均成绩为65，方差是4，求两组成绩的总平均数 $\bar{z}$ 和总方差 $s ^{2}$ .

查看解析
20、将四个半径为 $2$ 的小球放入一个大球中，则这个大球表面积的最小值为．

查看解析

上一页 1361 1362 1363 1364 1365 下一页跳转

$X$	0	1	2	3
$P$	$q$	0.2	0.1	0.2

$x$	3	4	5	6
$y$	2.5	3	4	4.5