相关试卷
-
1、对于任意的两个向量 , , , 下列命题一定正确的是( )A、 B、 C、 D、
-
2、已知是边长为1的正的边上的动点,为的中点,则的取值范围是( )A、 B、 C、 D、
-
3、已知 , , 且 , 则与的夹角为( )A、0° B、90° C、135° D、180°
-
4、如图,在矩形中,为中点,那么向量等于( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
5、若角的终边与单位圆的交点坐标是 , 则( )A、 B、 C、 D、
-
6、下列向量组中,能作为表示它们所在平面内的所有向量的基底的是( )A、 , B、 , C、 , D、 ,
-
7、如图,斜三棱柱中,底面是正三角形,分别是侧棱上的点,且 , 设直线与平面所成的角分别为 , 平面与底面所成的锐二面角为 , 则( )
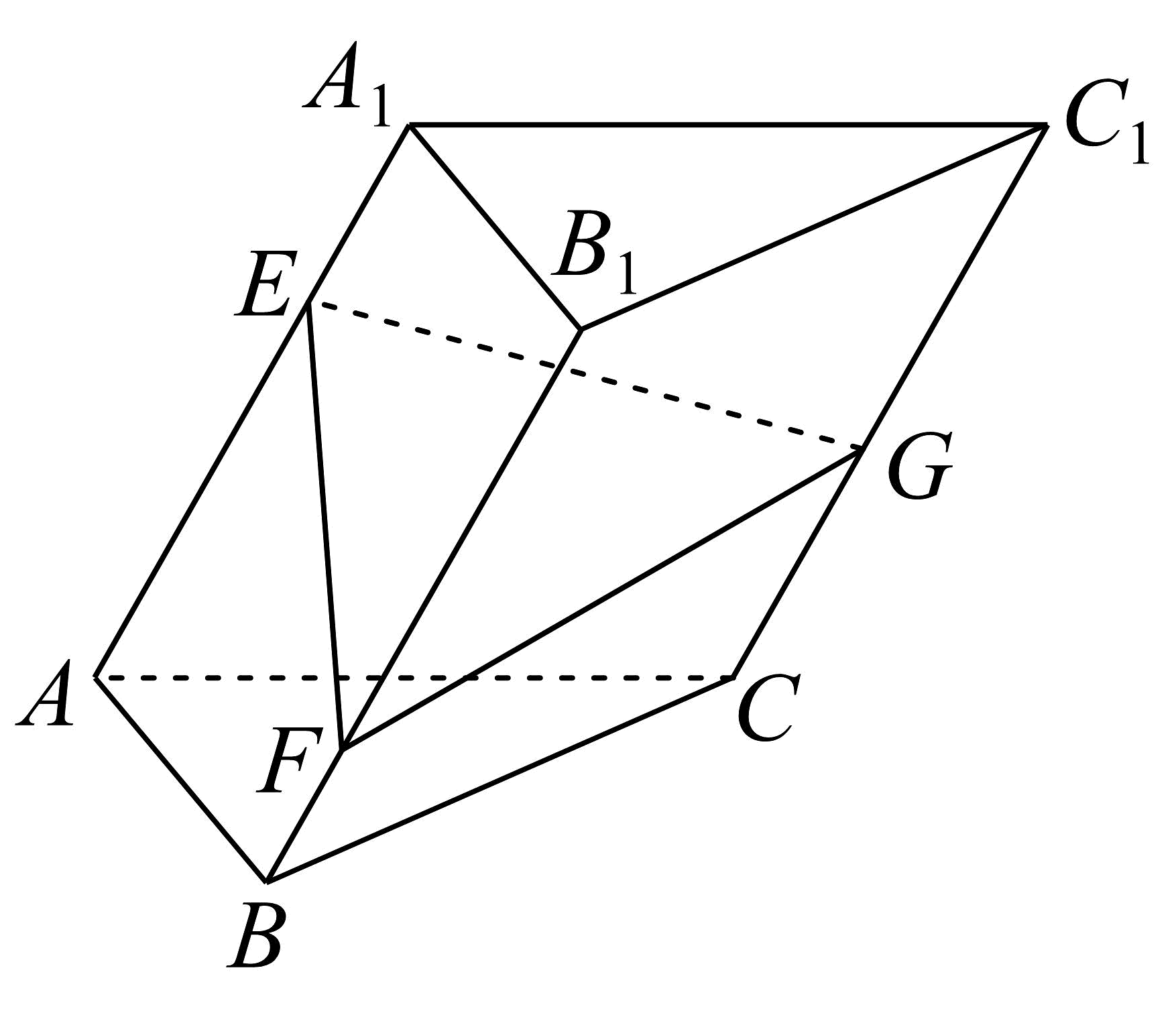 A、 B、 C、 D、
A、 B、 C、 D、 -
8、在中,角、、所对的边分别为、、 , 且 , .(1)、求;(2)、若为锐角三角形,求的面积范围.
-
9、已知正的边长为1,中心为 , 过的动直线与边分别相交于点 .
 (1)、若 , 求 .(2)、求与的面积之比的最小值.
(1)、若 , 求 .(2)、求与的面积之比的最小值. -
10、已知角是的内角,若 , .
(1)若 , 求角A的值;
(2)设 , 当取最大值时,求在上的投影向量(用坐标表示).
-
11、已知复数( , 为虚数单位).(1)、当时,求;(2)、设为复数z的共轭复数,若不是纯虚数,求m的取值范围.
-
12、已知 , , 向量 , 的夹角为 , 则 .
-
13、在中,角 , , 所对的边分别为 , , , 点为所在平面内点,满足 , 下列说法正确的有( )A、若 , 则点为的重心 B、若 , 则点为的外心 C、若 , , , 则点为的内心 D、若 , , , 则点为的垂心
-
14、已知菱形的对角线相交于点 , 点为的中点,若 , , 则( )A、 B、 C、 D、
-
15、如图所示,为测一树的高度,在地面上选取A,B两点,从A,B两点分别测得树尖的仰角为 , 且A,B两点之间的距离为6 m,则树的高度为( )
 A、 m B、 m C、 m D、 m
A、 m B、 m C、 m D、 m -
16、已知向量满足 , , 且 , 则与的夹角的余弦值为A、 B、 C、 D、
-
17、已知复数 , , 则( )A、 B、 C、0 D、1
-
18、已知函数 .(1)、求曲线在点处的切线方程;(2)、求证:;
-
19、为纪念五四青年运动105周年,进一步激励广大团员青年继承和发扬五四精神,宁波市教育局组织中小学开展形式多样、内容丰富、彰显青年时代风貌的系列主题活动.某中学开展“读好红色经典,争做强国少年”经典知识竞赛答题活动,现从该校参加竞赛的全体学生中随机选取100份学生的答卷作为样本,所有得分都分布在 , 将得分数据按照 , , …,分成7组,得到如图所示的频率分布直方图.
 (1)、估计该中学参加竞赛学生成绩的平均分(注:同一组中的数据用该组区间的中点值作代表);(2)、估计该中学参加竞赛学生成绩的第75百分位数(结果精确到0.1);(3)、若竞赛得分100分及以上的学生视为“强国少年”.根据选取的100份答卷数据统计;竞赛得分在内学生的平均分和方差分别为110和9,竞赛得分在内学生的平均分和方差分别为128和6,请估计该中学“强国少年”得分的方差.
(1)、估计该中学参加竞赛学生成绩的平均分(注:同一组中的数据用该组区间的中点值作代表);(2)、估计该中学参加竞赛学生成绩的第75百分位数(结果精确到0.1);(3)、若竞赛得分100分及以上的学生视为“强国少年”.根据选取的100份答卷数据统计;竞赛得分在内学生的平均分和方差分别为110和9,竞赛得分在内学生的平均分和方差分别为128和6,请估计该中学“强国少年”得分的方差. -
20、如图,在三棱锥中, , , , , 点在上,点为的中点.
 (1)、求证:平面平面;(2)、求与平面所成角的正弦值.
(1)、求证:平面平面;(2)、求与平面所成角的正弦值.