相关试卷
-
1、如图,在中, , , , , , 设与交于点 , 且 .
 (1)、求的值;(2)、定义平面非零向量之间的一种运算“”:(其中是两非零向量和的夹角).
(1)、求的值;(2)、定义平面非零向量之间的一种运算“”:(其中是两非零向量和的夹角).(ⅰ)若为的中点,求的值;
(ⅱ)若 , 求的值.
-
2、(用坐标法不给分)已知平行六面体所有棱长均为 .
 (1)、求证:平面平面;(2)、设平面与平面交于直线 , 求证:直线平面;(3)、求二面角的平面角的正弦值.
(1)、求证:平面平面;(2)、设平面与平面交于直线 , 求证:直线平面;(3)、求二面角的平面角的正弦值. -
3、某商店举行促销抽奖活动,在一个不透明袋子中放有6个大小质地完全相同的球,其中()个为红球,其余均为白球,现从中不放回地依次随机摸出2个球,若取到的两个球同色,则称为中奖,可以领取一张优惠券;若取到的两个球不同色,则称为不中奖.一次抽奖结束后,取出的球放回袋子中,供下一位顾客抽奖(每位顾客只有一次抽奖机会).(1)、若 , 求一次抽奖中奖的概率;(2)、若要求一次抽奖中奖的概率最小.
(ⅰ)求;
(ⅱ)求两位顾客抽奖至少有一位顾客中奖的概率.
-
4、在中,内角所对的边分别为 .(1)、若 , 且的面积为 , 求;(2)、若的平分线交于 , 求的长.
-
5、2025年春节期间国产动漫电影《哪吒之魔童闹海》火爆全世界,引起人们对中国动漫产业的关注.为了解中国动漫市场受市场群体关注的年龄(单位:岁)占比情况,某电影院调查了某天观看中国动漫系列电影的观众年龄情况,并按年龄进行适当分组(每组为左闭右开的区间),得到频率分布直方图如图所示(同一组的数据用该区间的中点值代表).
 (1)、求的值;(2)、求该样本的平均数和中位数 .
(1)、求的值;(2)、求该样本的平均数和中位数 . -
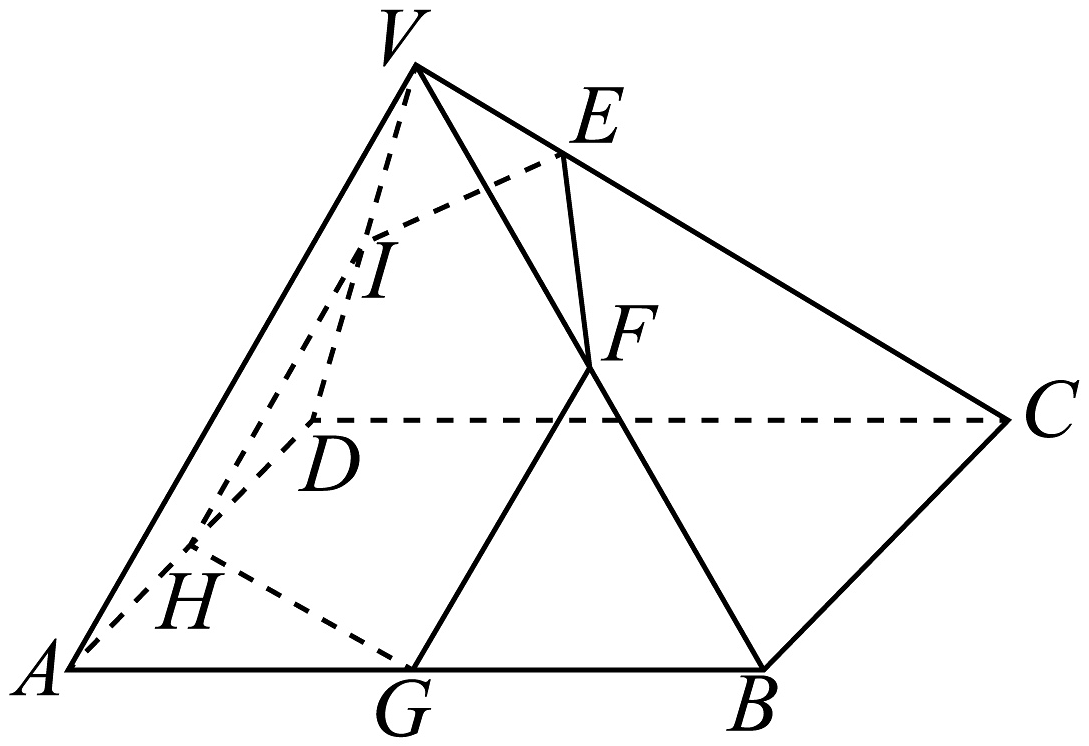
6、如图,在棱长均为4的正四棱锥中, , 若过点且垂直于棱的平面分别交棱于点 , 则五边形的面积为 .
-
7、如图,小明为了测量河对岸的塔高 , 选取了与塔底在同一水平面内的两个测量基点与 . 现测得 , 则塔高 .

-
8、设是一个随机试验中的两个事件,记为事件的对立事件,若 , 且与相互独立,则 .
-
9、在中,内角所对的边分别为 , 若在上的投影向量为 , 则( )A、 B、 C、 D、
-
10、已知复数均不为零,则( )A、 B、 C、 D、
-
11、如图,在圆锥中, , 点为线段上的动点,则( )
 A、 B、圆锥的侧面积为 C、直线与所成角为 D、当为线段中点时,直线与平面所成角的正弦值最大
A、 B、圆锥的侧面积为 C、直线与所成角为 D、当为线段中点时,直线与平面所成角的正弦值最大 -
12、一个棱长为6的正方体纸盒内有一个正四面体,若正四面体可以在纸盒内任意转动,则正四面体体积的最大值为( )A、 B、 C、 D、
-
13、在中,内角所对的边分别为 , 若 , 且 , 则( )A、 B、 C、 D、
-
14、已知是两个垂直的单位向量.若 , 设向量的夹角为 , 则( )A、 B、 C、 D、
-
15、柜子里有3双不同的手套,现从中随机地取出2只.若表示事件“取出的手套是一只左手一只右手的,但不是一双手套”,表示事件“取出的手套都是右手的”,表示事件“取出的手套不成双”,则( )A、 B、 C、 D、
-
16、已知直线与平面 , 则能使的充分条件是( )A、 B、 C、 D、
-
17、已知 , 则的虚部为( )A、 B、1 C、 D、2
-
18、已知三点共线,则( )A、1 B、3 C、 D、
-
19、某市有大型超市20家、中型超市60家、小型超市120家.为掌握各类超市的营业情况,现用比例分配的分层随机抽样方法抽取一个样本容量为20的样本,则抽取中型超市的数量为( )A、12 B、6 C、4 D、2
-
20、在中,角A,B,C的对边分别是a,b,c,已知 .(1)、求角A;(2)、点M在线段上,且满足 . 若 , 求的面积.