相关试卷
-
1、在三个地区暴发了流感,这三个地区分别有的人患了流感,假设这三个地区的人口数之比为 , 现从这三个地区中任意选取一个人,下列结论正确的是( )A、若此人选自地区,则其患流感的概率为0.05 B、此人患流感的概率为0.0485 C、若此人患流感,则其选自地区的概率为 D、若此人患流感,则其选自地区的概率为
-
2、已知 , 则下列说法正确的是( )A、 B、 C、 D、
-
3、已知数列: , 从中任选三项组成一个新数列,则所有新数列中的最小项之和为( )A、 B、 C、 D、
-
4、已知函数的图象在点处的切线的倾斜角为 , 则曲线在点处的切线的方程为( )A、 B、 C、 D、
-
5、已知 , 若 , 则( )A、-1 B、-2 C、11.8 D、2
-
6、如图,要让电路从处到处只有一条支路接通,则不同的路径有( )
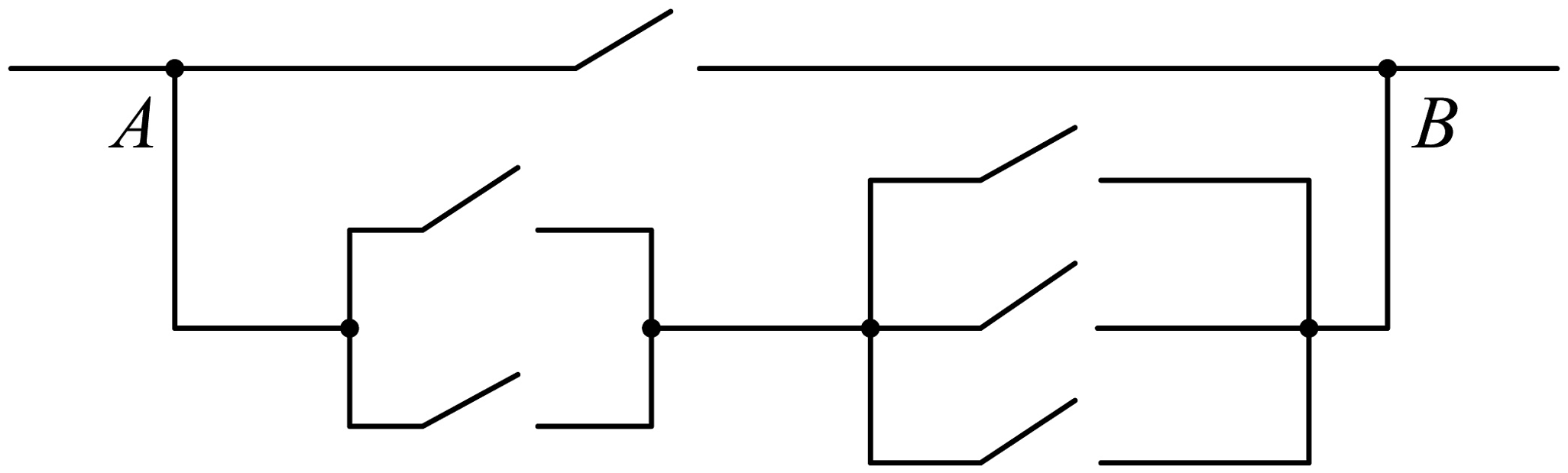 A、5种 B、6种 C、7种 D、9种
A、5种 B、6种 C、7种 D、9种 -
7、某班级有名学生,其中男生、女生的人数及是否喜爱篮球的人数如表所示,从这名学生中随机选择人作为体育课代表,若选到的学生喜爱“篮球”,则该学生是女生的概率为( )
喜爱“篮球”
不喜爱“篮球”
合计
男生
女生
合计
A、 B、 C、 D、 -
8、某活动室有足球和篮球,从中随机挑选2个球,若这2个球中足球个数为 , 且的分布列如下表所示,则( )
0
1
2
A、 B、 C、 D、 -
9、已知 , 则的值为( )A、-1 B、-2 C、0 D、2
-
10、( )A、8 B、13 C、63 D、66
-
11、在中,角A,B,C所对的边分别为a,b,c,且 .
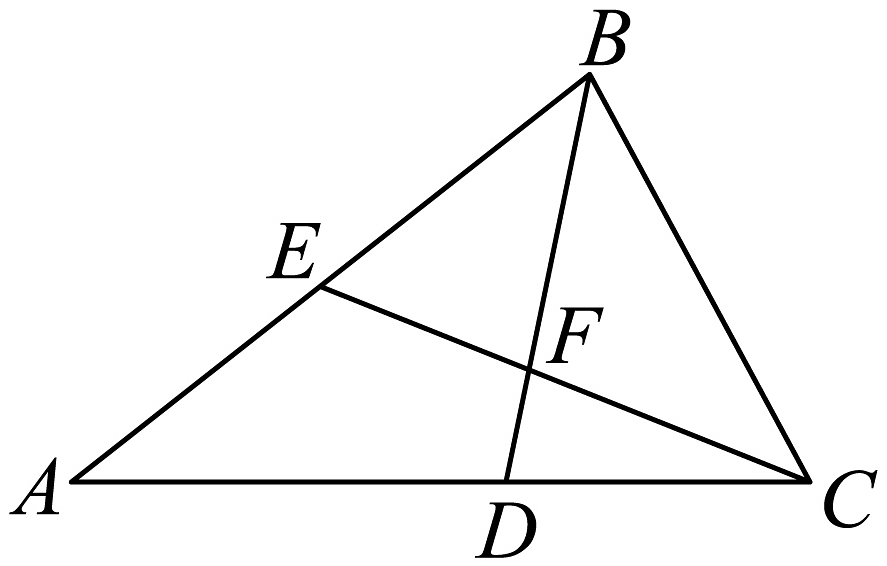 (1)、求角B;(2)、如图,的角平分线交于点D,且 , ,
(1)、求角B;(2)、如图,的角平分线交于点D,且 , ,(i)求的长度;
(ii)若边上的中线与相交于点F,求的余弦值.
-
12、某校举办环保知识竞赛,初赛中每位参赛者有三次答题机会,每次回答一道题,若答对,则通过初赛,否则直到三次机会用完.已知甲、乙、丙都参加了这次环保知识竞赛,且他们每次答对题目的概率都是 , 假设甲、乙、丙每次答题是相互独立的,且甲、乙、丙的答题结果也是相互独立的.(1)、求甲第二次答题通过初赛的概率;(2)、求乙通过初赛的概率;(3)、求甲、乙、丙三人中恰有两人通过初赛的概率.
-
13、如图,正三棱柱中,是的中点, .
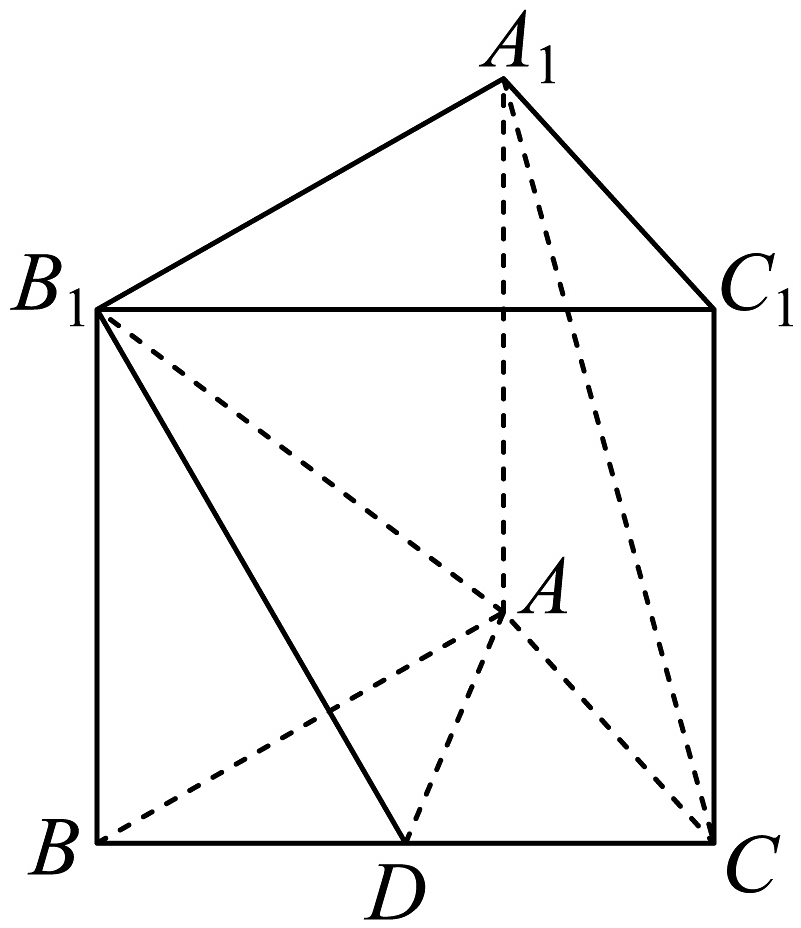 (1)、求证:平面;(2)、若三棱锥的体积为 , 求 .
(1)、求证:平面;(2)、若三棱锥的体积为 , 求 . -
14、在对某中学高一年级学生体重(单位:kg)的调查中,按男、女生人数比例用分层随机抽样的方法抽取部分学生进行测量,已知抽取的男生有50人,其体重的平均数和方差分别为54,20,抽取的女生有40人,其体重的平均数和方差分别为45,11,则估计该校高一年级学生体重的方差为 .
(参考公式:已知总体分为两层,各层的样本量,平均数,方差分别为m, , ;n, , , 记总的样本平均数和样本方差为 , , 其中 .
-
15、某商场为优化服务,对顾客做满意度问卷调查,满意度采用计分制(满分100).现随机抽取了其中10个数据依次为80,85,86,89,91,92,93,95,95,96,则这组数据的第25百分位数为 .
-
16、如图,正方体的棱长为1,P为的中点,Q为线段上的动点,过点A,P,Q的平面截该正方体所得截面记为S,则下列命题正确的是( )
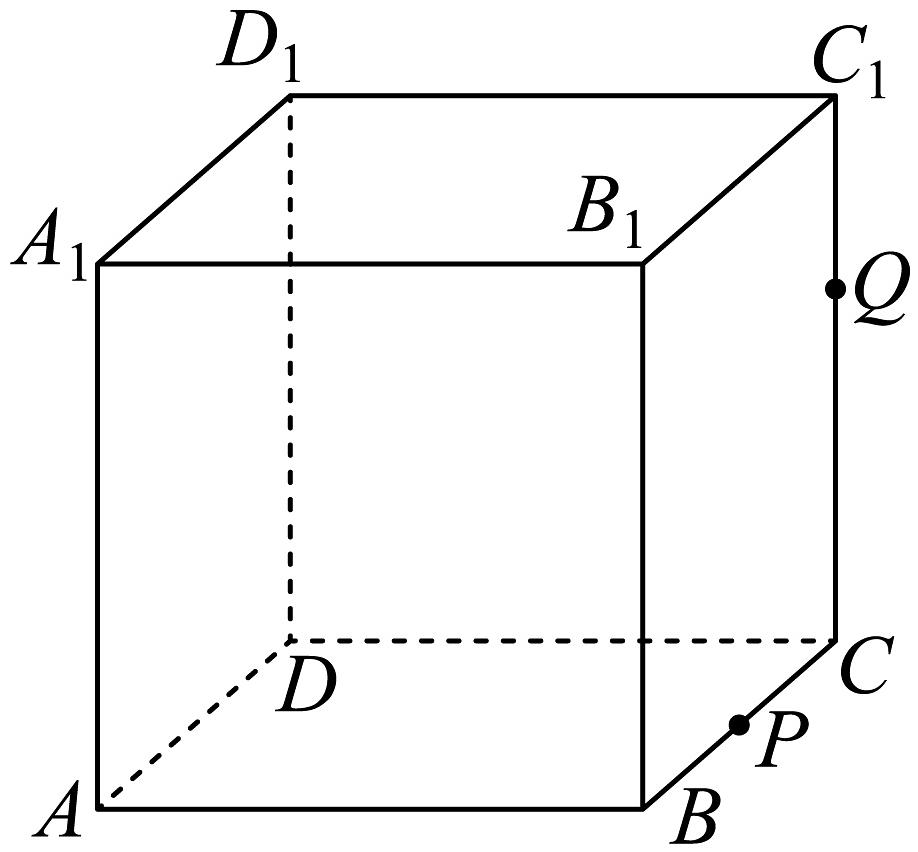 A、直线与直线所成角的正切值为 B、当时,截面S的形状为等腰梯形 C、当时,S与交于点R,则 D、当时,直线与平面的夹角正弦值的取值范围是
A、直线与直线所成角的正切值为 B、当时,截面S的形状为等腰梯形 C、当时,S与交于点R,则 D、当时,直线与平面的夹角正弦值的取值范围是 -
17、已知为虚数单位,以下四个说法中正确的是( )A、 B、若 , 则复平面内对应的点位于第二象限 C、复数 , D、若复数满足 , 则的最大值为6
-
18、抛一枚质地均匀的骰子两次,设事件表示“第二次朝上的数字为偶数”,则下列事件中与事件相互独立的是( )A、第二次朝上的数字是奇数 B、第二次朝上的数字为2 C、两次朝上的数字之和为9 D、两次朝上的数字之和为10
-
19、已知两个单位向量满足 , 则( )A、0 B、 C、1 D、2
-
20、如图,空间四边形中, , , , 点在线段上,且 , 点为中点,则等于( )
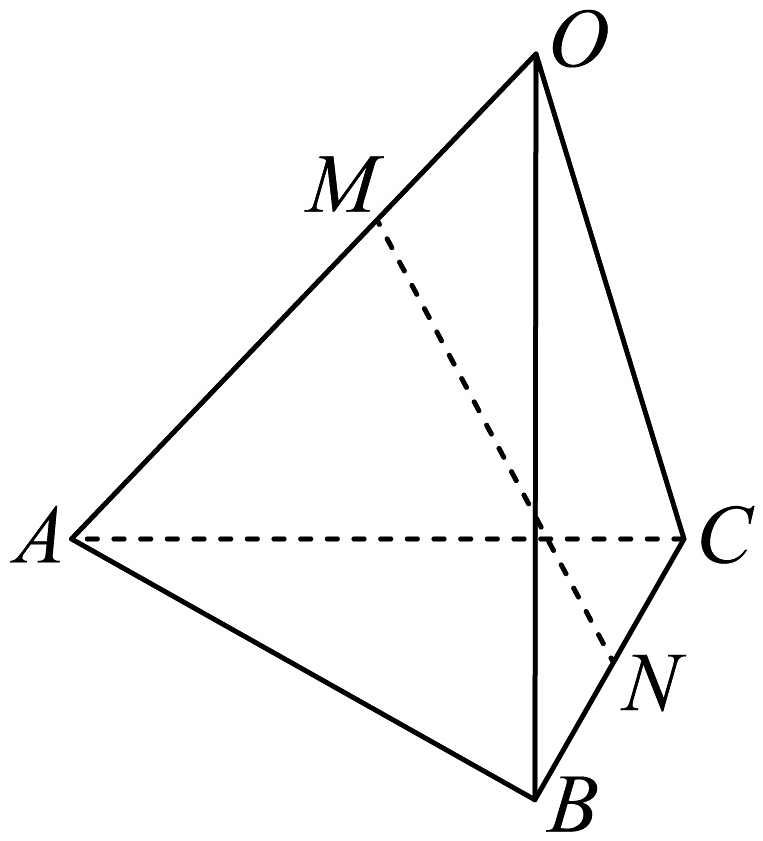 A、 B、 C、 D、
A、 B、 C、 D、