相关试卷
-
1、在内函数的定义域是( )A、 B、 C、 D、
-
2、已知函数 , 其中为自然对数的底数.(1)、讨论的单调性;(2)、若方程有两个不同的根 .
(i)求的取值范围;
(ii)证明: .
-
3、已知函数.(1)、求的最小正周期及单调递增区间;(2)、若方程在上有两个不相等的实数根,则实数的取值范围.
-
4、已知1是函数(a,b,)的极值点,在处的切线与直线垂直.(1)、求a,b的值;(2)、若函数在上有最大值2,在上有最小值也有最大值,求实数m的取值范围.
-
5、已知函数.(1)、完善下面的表格并作出函数在上的图象:
0
1
 (2)、将函数的图象向右平个单位后再向上平移1个单位得到的图象,解不等式.
(2)、将函数的图象向右平个单位后再向上平移1个单位得到的图象,解不等式. -
6、已知函数的图象过点 , 若在内有5个零点,则的取值范围为.
-
7、已知 , , , 则.
-
8、已知函数为奇函数,则实数的值为.
-
9、已知函数 , 则下列结论正确的是( )A、的图象关于轴对称 B、的图象关于点对称 C、的图象关于直线对称 D、是的极大值点
-
10、已知 , 则下列说法正确的是( )A、若 , 则 B、若 , 则 C、若 , , 则的最大值为 D、 , , 使得
-
11、如果关于的不等式的解集为 , 那么下列数值中,可取到的数为( )A、 B、0 C、1 D、2
-
12、已知直线是函数图象的任意两条对称轴,且的最小值为 , 则的单调递增区间是( )A、 B、 C、 D、
-
13、已知(且)是上的奇函数,且(1)、求的解析式;(2)、把区间等分成份,记等分点的横坐标依次为 , , 记 , 是否存在正整数n,使不等式有解?若存在,求出所有n的值,若不存在,说明理由;(3)、函数在区间上的值域是 , 求的取值范围.
-
14、已知 , 且 , 则( )A、 B、 C、 D、
-
15、如图,在四棱锥中,底面是正方形,侧棱底面 , , 是的中点,作交于点 .
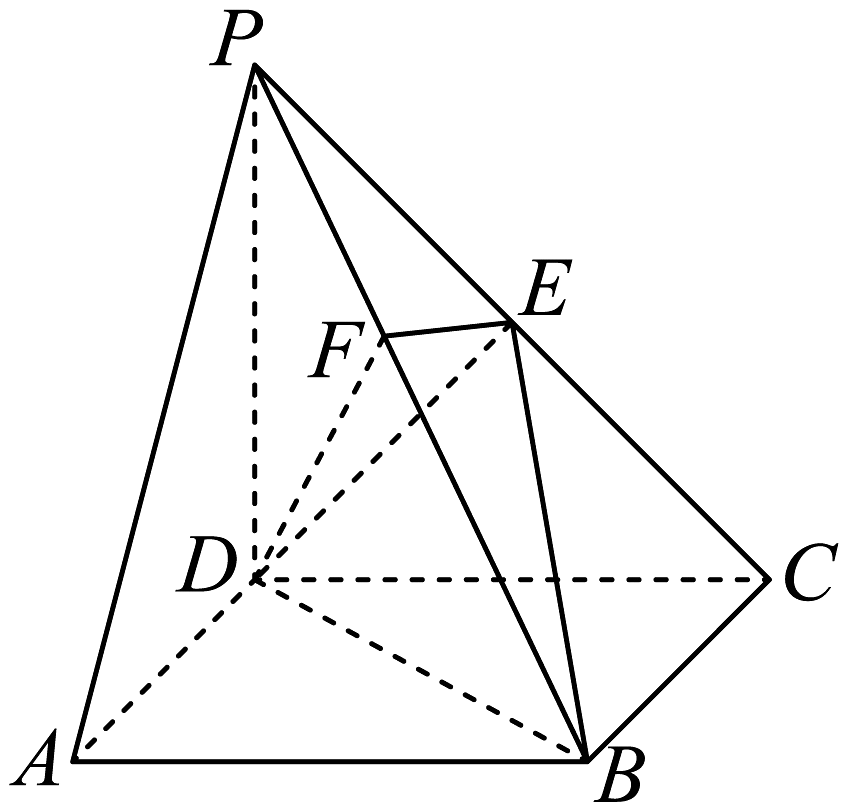 (1)、求证:面;(2)、求平面与平面的夹角的大小;(3)、求点到平面的距离.
(1)、求证:面;(2)、求平面与平面的夹角的大小;(3)、求点到平面的距离. -
16、若 , , , 则以下不等式正确的是( )A、 B、 C、 D、
-
17、已知定义域为的函数是奇函数。(1)、求的值(2)、判断并证明该函数在定义域上的单调性(3)、若对任意的 , 不等式恒成立,求实数的取值范围.
-
18、已知函数 , .若的零点恰为的零点,则a的最大值是.
-
19、已知抛物线的焦点为F,斜率为1的直线l过F与C交于A,B两点,AB的中点到抛物线准线的距离为8,则 .
-
20、已知平面向量 , , 则( )A、当时, B、若 , 则 C、若 , 则 D、若与的夹角为钝角,则