相关试卷
-
1、在扇形中, , 且弦 , 则扇形的面积为( )A、 B、 C、 D、
-
2、如图,四边形为梯形, , 四边形为平行四边形.
 (1)、求证:∥平面;(2)、若平面 , 求:
(1)、求证:∥平面;(2)、若平面 , 求:(ⅰ)直线与平面所成角的正弦值;
(ⅱ)点D到平面的距离.
-
3、在统计某学校所有选择理科和文科的学生数据中,发现理科生多于文科生,女生多于男生,则关于本次学生样本的数据中,结论一定成立的是( )A、理科男生多于文科女生 B、文科女生多于文科男生 C、理科女生多于文科男生 D、理科女生多于理科男生
-
4、直线:与:交于点P,圆C:上有两动点A,B,且 , 则的最小值为( )A、 B、 C、 D、
-
5、(1)若对恒成立,求的值;
(2)求的值域;
(3)正五棱锥的所有棱长均为 , 求此正五棱锥的表面积.
-
6、如图,四棱锥中,底面是边长为4的菱形, , , E为中点,与交点为O.
 (1)、求证:平面;(2)、求证:平面平面;(3)、若 , 求点C到平面的距离.
(1)、求证:平面;(2)、求证:平面平面;(3)、若 , 求点C到平面的距离. -
7、在中,角A,B,C的对边分别为a,b,c,若 .
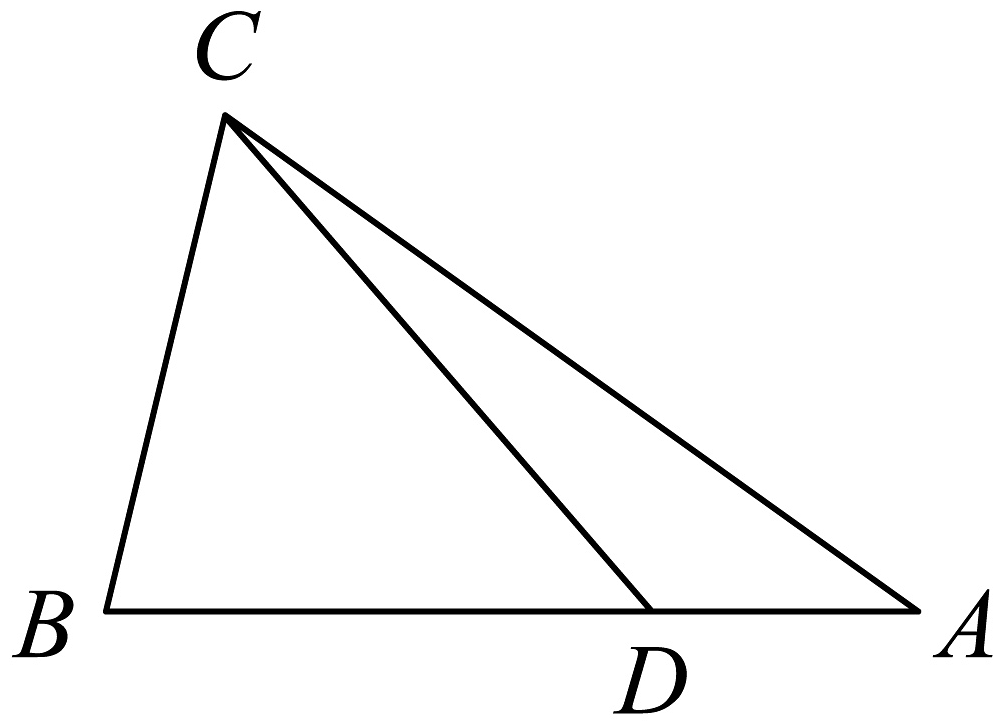 (1)、求角C的大小;(2)、设D是上一点,且 , , 且 , 求的面积.
(1)、求角C的大小;(2)、设D是上一点,且 , , 且 , 求的面积. -
8、如图,边长为6的正中,点D在边上,且 , 点M在线段上.
 (1)、若 , 求的值;(2)、若 , 求x及的值.
(1)、若 , 求的值;(2)、若 , 求x及的值. -
9、已知函数 , 其中 , 且函数的图象的对称中心与对称轴的距离的最小值为 .(1)、求的解析式;(2)、求在区间上的值域.
-
10、欧拉公式:(i是虚数单位,)是由瑞士著名数学家欧拉发现的,被誉为“数学中的天桥”.根据欧拉公式,可求出的最大值为 .
-
11、的内心为P,外心为O,重心为G,若 , , 下列结论正确的是( )A、的内切圆半径为 B、 C、 D、
-
12、下列命题正确的是( )A、一个三棱锥被过三条侧棱的中点的平面所截,截得的两部分为一个三棱台和一个小三棱锥,则此三棱台与小三棱锥的体积比为7 B、圆锥被过其顶点的某平面所截,截面形状为一个三角形,若圆锥的底面半径 , 高 , 则截面三角形面积的最大值为48 C、圆锥被过其顶点的某平面所截,截面形状为一个三角形,若圆锥的底面半径 , 高 , 则截面三角形面积的最大值为48 D、若一个平行六面体被某平面所截,所得截面形状为四边形,则此四边形至少有一组对边互相平行
-
13、设都是复数,i是虚数单位,则下列结论中一定成立的是( )A、方程无复数解 B、若 , 则 C、 D、
-
14、四面体中,若 , , , 则此四面体的外接球的表面积为( )A、 B、 C、 D、
-
15、八角星纹是大汶口文化中期彩陶纹样中具有鲜明特色的花纹.八角星纹常绘于彩陶盆和豆的上腹,先于器外的上腹施一圈红色底衬,然后在上面绘并列的八角星形的单独纹样.八角星纹以白彩的成,黑线勾边,中为方形或圆形,且有向四面八方扩张的感觉.八角星纹延续的时间较长,传播范围亦广,在长江以南的时间稍晚的崧泽文化的陶豆座上也屡见刻有八角大汶口文化八角星纹.图2是图1抽象出来的图形,在图2中,圆中各个三角形(如△ACD)为等腰直角三角形,点O为圆心,中间部分是正方形且边长为2,定点A,B所在位置如图所示,则的值为( )
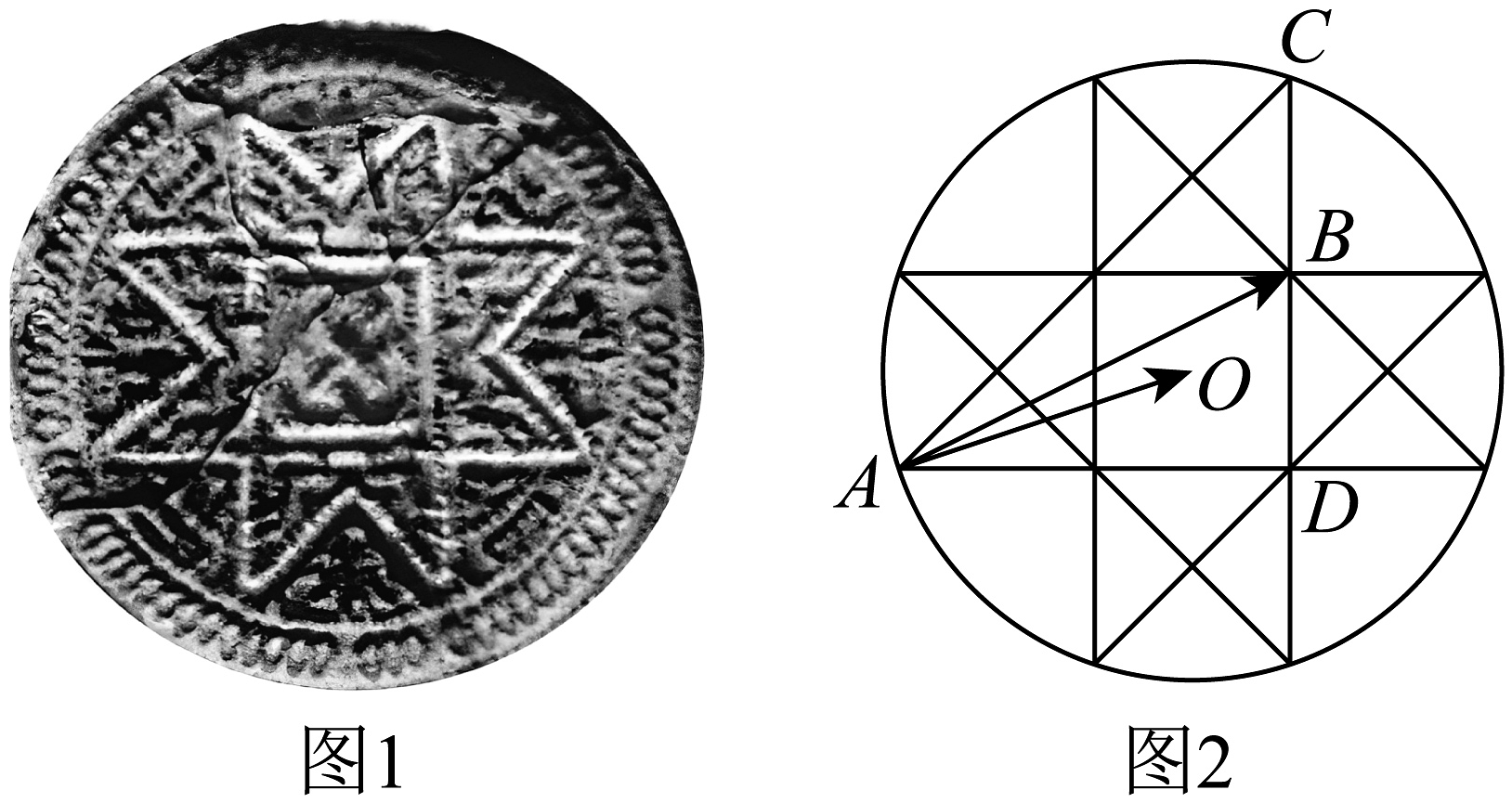 A、14 B、12 C、10 D、8
A、14 B、12 C、10 D、8 -
16、中,角所对的边分别为 , , , 交于点 , 且 , 则的值为( )
 A、 B、 C、6 D、3
A、 B、 C、6 D、3 -
17、在直角坐标平面内,已知 , , , , 以y轴为旋转轴,将四边形ABCD旋转一周,得一个旋转体,则此旋转体的表面积为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
18、在正四棱锥的所有棱长均相等,E为的中点,则异面直线与所成角的余弦值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
19、将函数图象上的所有点的横坐标变为原来的倍(纵坐标不变),再将图象向左平移后得函数的图象,则函数的解析式为( )A、 B、 C、 D、
-
20、在直角坐标平面内,的三顶点的坐标分别为 , , , 则的面积为( )
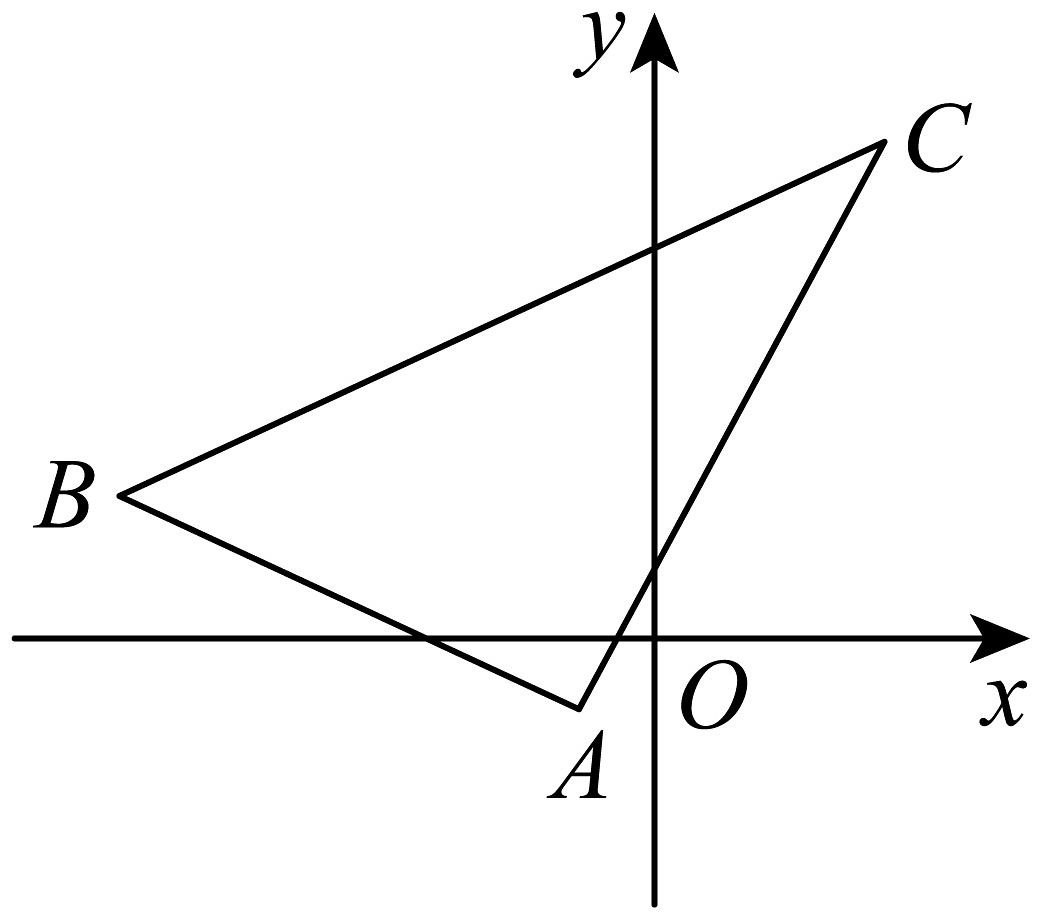 A、120 B、60 C、30 D、15
A、120 B、60 C、30 D、15