相关试卷
-
1、已知偶函数在区间上单调递增且存在最大值为 , 则函数在区间上( )A、单调递增且最大值为 B、单调递增且最小值为 C、单调递减且最大值为 D、单调递减且最小值为
-
2、函数的图象大致是( )A、
 B、
B、 C、
C、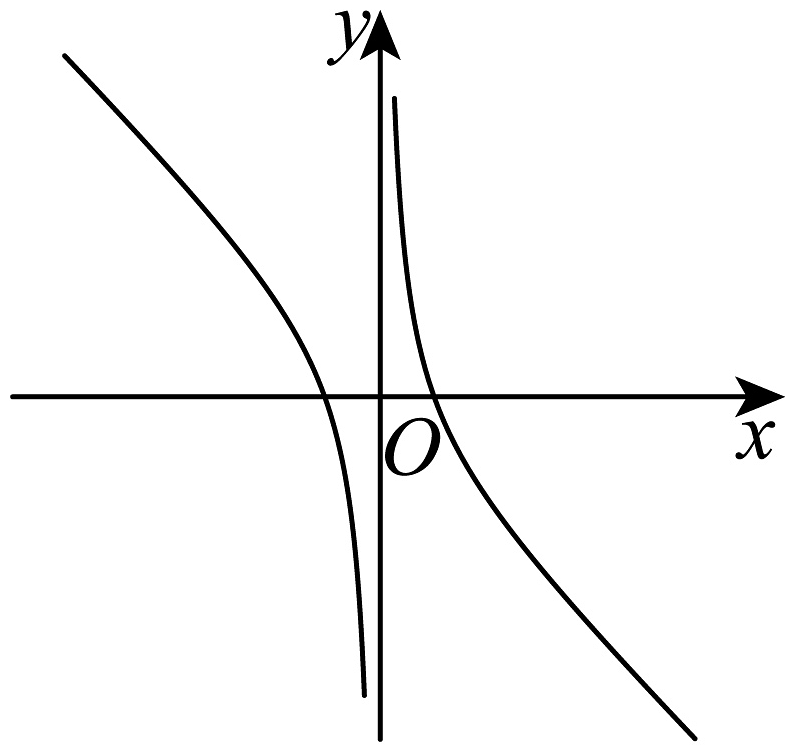 D、
D、
-
3、命题“ , ”的否定是( )A、 , B、 , C、 , D、 ,
-
4、已知集合 , 则( )A、 B、 C、 D、
-
5、已知空间中三点 , 则下列说法正确的是( )A、 B、与是共线向量 C、和夹角的余弦值是1 D、与同向的单位向量是
-
6、已知双曲线的一条渐近线方程为 , 焦点到渐近线的距离为.(1)、求双曲线的方程;(2)、设为坐标原点,若直线过点 , 与双曲线的左、右两支分别交于A,B两点,且的面积为 , 求直线的方程.
-
7、“九子游戏”是一种传统的儿童游戏,它包括打弹子、滚圈子、踢毽子、顶核子、造房子、拉扯铃子、刮片子、掼结子、抽陀子九种不同的游戏项目,某小学为丰富同学们的课外活动,举办了“九子游戏”比赛,所有的比赛项目均采用局胜的单败淘汰制,即先赢下局比赛者获胜.造房子游戏是同学们喜爱的项目之一,经过多轮淘汰后,甲、乙二人进入造房子游戏的决赛,已知每局比赛甲获胜的概率为 , 乙获胜的概率为.(1)、若 , 设比赛结束时比赛的局数为 , 求的分布列与数学期望;(2)、现有两种赛制:赛制一:采用3局2胜制,赛制二:采用5局3胜制,乙选手要想获胜概率大,应选哪种赛制?并说明理由.
-
8、在中,角A, , 所对的边分别为 , , , . 且 , 则 .
-
9、已知点为平面内不同的四点,若 , 且 , 则
-
10、已知数列的前项和为 , 且 , 若 , 则( )A、是等比数列 B、是等比数列 C、是等差数列 D、是等差数列
-
11、如图,在边长为4的正方体ABCD-A1B1C1D1中,E,F分别是棱B1C1 , C1D1的中点,P是正方形A1B1C1D1内的动点,则下列结论正确的是( )
 A、若DP∥平面CEF,则点P的轨迹长度为 B、若AP= , 则点P的轨迹长度为 C、若AP= , 则直线AP与平面CEF所成角的正弦值的最小值是 D、若Р是棱A1B1的中点,则三棱锥的外接球的表面积是
A、若DP∥平面CEF,则点P的轨迹长度为 B、若AP= , 则点P的轨迹长度为 C、若AP= , 则直线AP与平面CEF所成角的正弦值的最小值是 D、若Р是棱A1B1的中点,则三棱锥的外接球的表面积是 -
12、若 , 则( )A、 B、 C、 D、
-
13、已知四面体的各个面均为全等的等腰三角形,且.设为空间内一点,且五点在同一个球面上,若 , 则点的轨迹长度为( )A、 B、 C、 D、
-
14、已知在四边形中, , , , 则的长为( )A、 B、 C、 D、
-
15、已知圆关于直线对称,且过点.(1)、求证:圆与直线相切;(2)、若直线过点与圆交于、两点,且 , 求此时直线的方程.
-
16、数列的前项和为 ,
-
17、几何体结构素描是学习素描最重要的一个阶段.某同学在画“切面圆柱体”(用不平行于圆柱底面的平面去截圆柱,圆柱底面与截面之间的部分叫做切面圆柱体)的过程中,发现“切面”是一个椭圆,若切面所在平面与底面成角,则该椭圆的离心率为.

-
18、已知点P在双曲线的右支上, , 是双曲线的左、右焦点,则下列说法正确的是( )A、 B、离心率 C、渐近线方程为 D、点到渐近线的距离为3
-
19、已知数列的首项是1,其前项和是 , 且 , .(1)、求 , 的值及数列的通项公式;(2)、若存在实数 , 使得关于的不等式 , 有解,求实数取到最大值时的值.
-
20、现有一个抽奖活动,主持人将奖品放在编号为1、2、3的箱子中,甲从中选择了1号箱子,但暂时未打开箱子,主持人此时打开了另一个箱子(主持人知道奖品在哪个箱子,他只打开甲选择之外的一个空箱子).记表示第号箱子有奖品,表示主持人打开第号箱子.则下列说法正确的是( )A、 B、 C、若再给甲一次选择的机会,则甲换号后中奖概率增大 D、若再给甲一次选择的机会,则甲换号后中奖概率不变