相关试卷
-
1、已知集合(其中),(1)、求;(2)、当时,求;(3)、若 , 求实数的取值范围.
-
2、如图所示,以为始边作角与 , 它们的终边与单位圆分别交于两点,已知点的坐标为 , 点的坐标为.
 (1)、求的值;(2)、求的值.
(1)、求的值;(2)、求的值. -
3、若函数且是指数函数,其图象过点 , 则函数的单调递增区间为.
-
4、设函数 , 则.
-
5、已知弧长为的弧所对的圆心角为 , 则该弧所在的扇形面积为.
-
6、函数的部分图象如图所示,则( )
 A、函数的图象关于点对称 B、该图象向左平移个单位长度可得图象 C、该图象的横坐标伸长到原来的2倍,纵坐标缩短到原来倍可得图象 D、函数在上单调递减
A、函数的图象关于点对称 B、该图象向左平移个单位长度可得图象 C、该图象的横坐标伸长到原来的2倍,纵坐标缩短到原来倍可得图象 D、函数在上单调递减 -
7、下列说法正确的是( )A、二次函数的零点是 B、函数与是同一函数 C、函数且的图象恒过点 D、若函数在上单调递增,则实数的取值范围是
-
8、下列四个式子中,计算正确的是( )A、 B、 C、 D、若 , 则
-
9、函数 , 若 , 且互不相等,则的取值范围是( )A、 B、 C、 D、
-
10、已知命题 , 命题 , 则( )A、和都是真命题 B、和都是真命题 C、和都是真命题 D、和都是真命题
-
11、某物流公司为了提高运输效率,计划在机场附近建造新的仓储中心.已知仓储中心建造费用(单位:万元)与仓储中心到机场的距离(单位)之间满足的关系为 , 则当最小时,的值为( )A、2080 B、40020 C、 D、20
-
12、函数是( )A、最小正周期为的奇函数 B、最小正周期为的偶函数 C、最小正周期为的奇函数 D、最小正周期为的偶函数
-
13、下列说法正确的是( )A、 B、 C、 D、
-
14、已知是直线的方向向量,是平面的法向量,若 , 则实数( )A、 B、 C、1 D、4
-
15、圆心为且与直线相切的圆的方程为( )A、 B、 C、 D、
-
16、在锐角中,角 , , 的对边为 , , , 若 , .
 (1)、求角的大小;(2)、若为的中点,且 , 求的面积;(3)、如图,过点在所在平面内作 , 且满足.求线段的最大值.
(1)、求角的大小;(2)、若为的中点,且 , 求的面积;(3)、如图,过点在所在平面内作 , 且满足.求线段的最大值. -
17、如图,在正三棱柱中, , 分别为棱 , 的中点,.
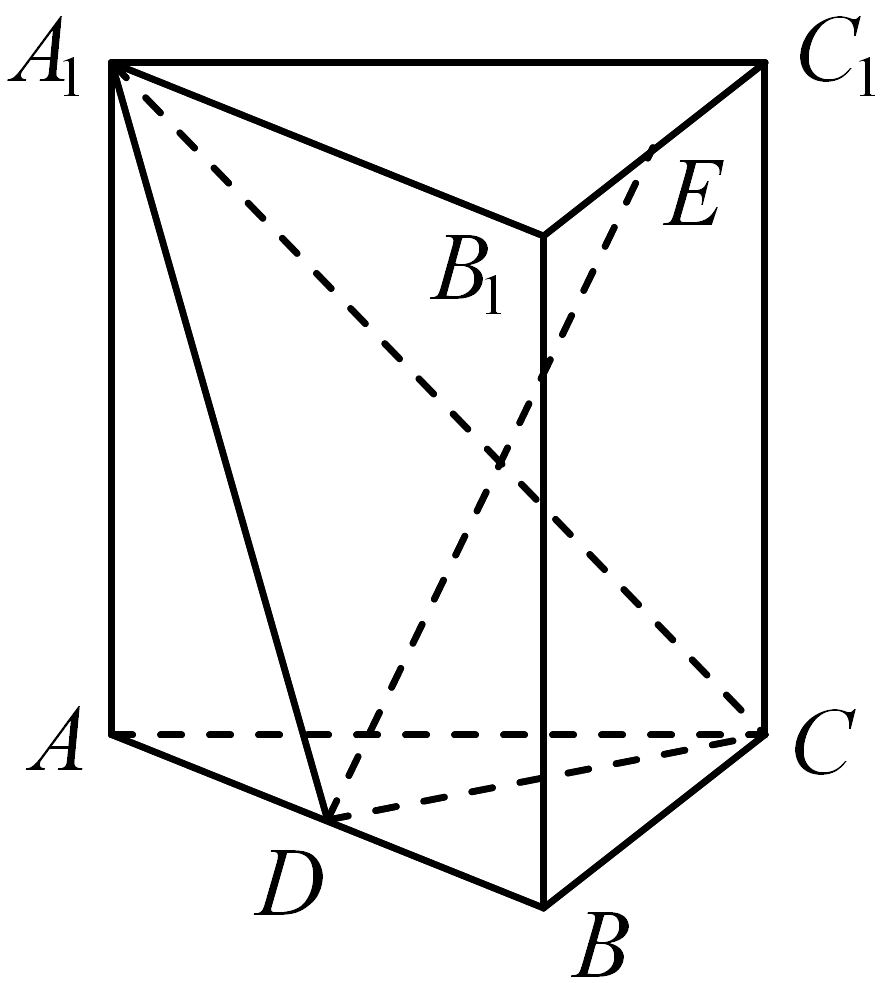 (1)、证明:平面;(2)、若三棱锥的体积为 , 求二面角的余弦值.
(1)、证明:平面;(2)、若三棱锥的体积为 , 求二面角的余弦值. -
18、“数学好玩”是国际著名数学家陈省身赠送给少年数学爱好者们的一句话.某校为了更好地培养学生创新精神和实践能力,激发学生钻研数学的兴趣和热情,特举办数学节活动.在活动中,共有20道数学问题,满分100分在所有的答卷中随机抽取100份作为样本,将样本的成绩分成六段: , , ……, , 得到如图所示的频率分布直方图.
 (1)、求频率分布直方图中a的值,并估计该校全体学生这次数学成绩的中位数;(2)、活动中,甲、乙、丙三位同学独立参加竞赛,已知甲同学答对了12道,乙同学答对了8道,丙同学答对了n道,假设每道数学问题难度相当,被答对的可能性都相同.
(1)、求频率分布直方图中a的值,并估计该校全体学生这次数学成绩的中位数;(2)、活动中,甲、乙、丙三位同学独立参加竞赛,已知甲同学答对了12道,乙同学答对了8道,丙同学答对了n道,假设每道数学问题难度相当,被答对的可能性都相同.(i)任选一道数学问题,求甲、乙两位同学恰有一人答对的概率;
(ii)任选一道数学问题,若甲、乙、丙三个人中至少有一个人答对的概率为 , 求n的值.
-
19、已知向量 , , 设.(1)、求的最小正周期;(2)、若 , , 求的值.
-
20、在圆台中,圆的半径是2,母线 , 圆是的外接圆, , , 则三棱锥体积最大值为 .