相关试卷
-
1、若存在满足 , 且 , 则称为函数的次不动点.
已知为常数且.
(1)、当时,判断是否为函数的次不动点,并说明理由;(2)、已知有两个次不动点 , ,①求的取值范围;
②若对任意 , 且 , , , , 求△的面积的取值范围.
-
2、已知为坐标原点,椭圆:()的左焦点为 , 且经过点 , 过点的直线与椭圆相交于、两点,且、在轴的同侧.(1)、求椭圆的标准方程;(2)、为的重心,直线、分别交轴于、两点,记和的面积分别为 , , 求的取值范围.
-
3、如图,等腰直角三角形中, , 是中点,、分别是、边上的动点,且 , 将沿折起,将点折至点的位置,得到四棱锥.
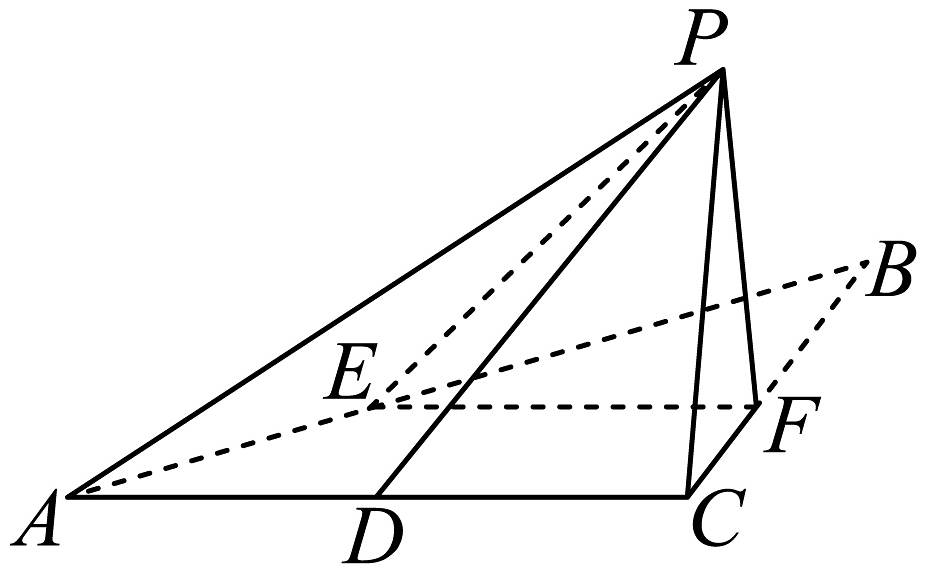 (1)、求证:;(2)、若 , 二面角是直二面角,求平面与平面夹角的余弦值;(3)、当时,是否存在这样的点 , 使得二面角为 , 且直线与平面所成角为 , 若存在,求出的长,若不存在,请说明理由.
(1)、求证:;(2)、若 , 二面角是直二面角,求平面与平面夹角的余弦值;(3)、当时,是否存在这样的点 , 使得二面角为 , 且直线与平面所成角为 , 若存在,求出的长,若不存在,请说明理由. -
4、已知为坐标原点,直线过定点 , 设圆的半径为2,圆心在直线:上.(1)、若圆心也在直线上,求过点与圆相切的直线方程;(2)、若圆上存在点 , 使得 , 求圆心的横坐标的取值范围.
-
5、在中,内角 , , 的对边分别为 , , , 且.(1)、求角的大小;(2)、已知 , , 求.
-
6、已知椭圆()的左焦点为 , 直线与椭圆交于点、 , 的周长最大值为 , 则椭圆离心率的最大值为.
-
7、在G5联盟考试成绩中,从某班随机抽取8名同学的数学成绩,分数从低到高为:70,77,90,101,115,119,138,149,则第70百分位数为.
-
8、已知正方体的棱长为1, , 是棱、的中点,动点满足 , 其中 , , , 则下列命题正确的是( )A、若 , , 则平面 B、若 , 则与所成角的取值范围为 C、若平面 , 则 D、若 , 则
-
9、已知双曲线:( , )的离心率为 , 焦距为 , 直线与双曲线交于、两点,点位于第一象限,过点作轴的垂线,垂足为 , 点为双曲线的左焦点,则( )A、若 , 则 B、若 , 则 C、若 , 则 D、
-
10、已知复数 , , 且 , 则以下四个命题正确的是( )A、 B、为纯虚数 C、为纯虚数 D、为虚数
-
11、已知抛物线:()的焦点到的距离为1,是抛物线上的动点,到的距离与之和的最小值为1,则点的轨迹围成的面积是( )A、 B、 C、 D、
-
12、曲线与在内有3个交点,则可能的值为( )A、4 B、3 C、2 D、1
-
13、已知 , 均为正实数, , 则的最大值为( )A、 B、 C、 D、
-
14、把一个圆锥分割成两个侧面积相等的小圆锥和圆台,则小圆锥和圆台的高之比为( )A、1 B、 C、2 D、
-
15、曲线: , 则“”是“曲线表示双曲线”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
16、已知直线: , : , 若 , 则( )A、 B、 C、4 D、1
-
17、直线的倾斜角为( )A、0 B、 C、 D、不存在
-
18、已知函数 .(1)、已知函数在点处的切线的倾斜角为 , 求的值.(2)、若函数为增函数,求的取值范围;(3)、已知 . 证明:;
-
19、某公司为考核员工,采用某方案对员工进行业务技能测试,并统计分析测试成绩以确定员工绩效等级.该公司统计了七个部门测试的平均成绩(满分100分)与绩效等级优秀率 , 如下表所示:
32
41
54
68
74
80
92
0.28
0.34
0.44
0.58
0.66
0.74
0.94
根据数据绘制散点图,初步判断,选用作为回归方程.令 , 经计算得 ,
(1)、已知某部门测试的平均成绩为60分,估计其绩效等级优秀率;(2)、根据统计分析,大致认为各部门测试平均成绩 , 其中近似为样本平均数 , 近似为样本方差 . 经计算 , 求某个部门绩效等级优秀率不低于的概率.参考公式与数据:
① .
②线性回归方程中, , .
③若随机变量 , 则 , , .
-
20、在中,内角的对边分别为 , 且 , .(1)、求的值;(2)、若的面积为 , 求边上的高.