版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、已知双曲线 $C : \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0, b > 0)$ 的左焦点为 $F_{1}, O$ 为坐标原点，若在 $C$ 的右支上存在关于 $x$ 轴对称的两点 $P, Q$ ，使得 $△ P F_{1} Q$ 为正三角形，且 $O Q ⊥ F_{1} P$ ，则 $C$ 的离心率为.

查看解析
2、已知空间中的三点 $A (- 2, 0, 2), B (- 1, 1, 2), C (- 3, 0, 4)$ ，则点 $B$ 到直线 $A C$ 的距离为．

查看解析
3、在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A B = B C = A A_{1} = 2$ ， $∠ A B C = 90 °$ ， $E$ ， $F$ 分别为棱 $A C$ 和 $C C_{1}$ 的中点， $D$ 为棱 $A_{1} B_{1}$ 上的动点，则（）

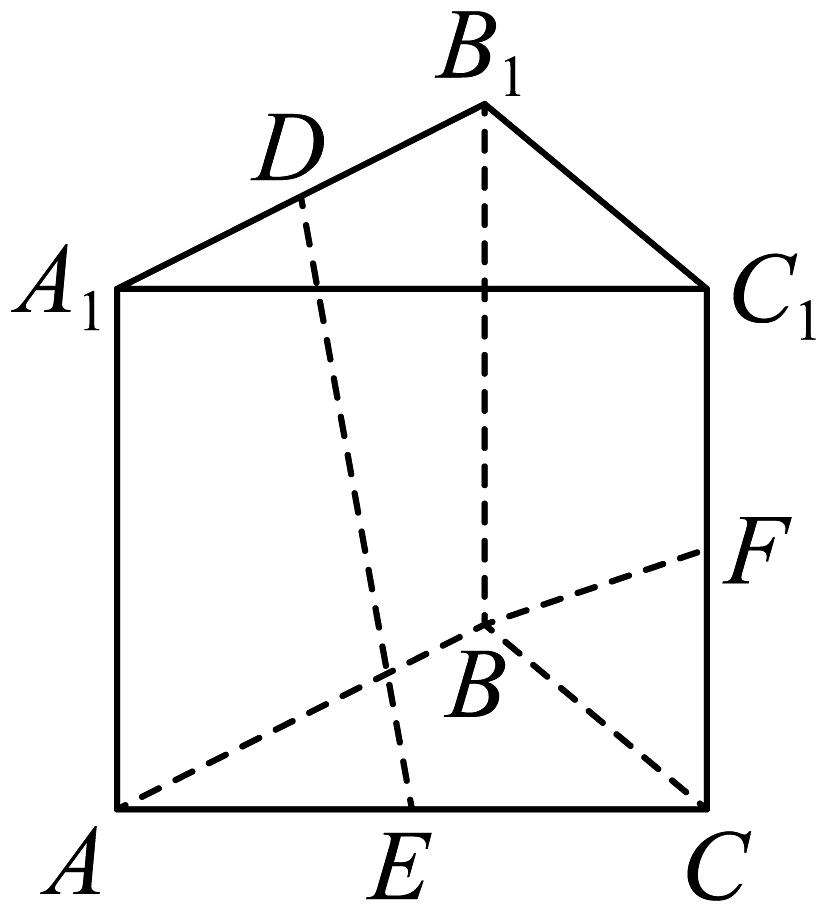A、 $B F ⊥ D E$ B、该三棱柱的体积为4 C、过 $A_{1}$ ， $B_{1}$ ， $E$ 三点截该三棱柱的截面面积为 $\sqrt{5}$ D、直线 $D E$ 与平面 $A B B_{1} A_{1}$ 所成角的正切值的最大值为 $\frac{1}{2}$

查看解析
4、已知直线l： $x - y + 5 = 0$ 与圆C： $x^{2} + y^{2} - 2 x - 7 = 0$ ，下列说法正确的是（）

A、点 $A (3, 1)$ 在圆C外 B、直线l与圆C相离 C、点P为圆C上的动点，点Q为直线l上的动点，则 $|P Q|$ 的取值范围是 $[\sqrt{2}, + \infty)$ D、将直线l下移4个单位后得到直线l＇，则圆C上有且仅有3个点到直线l＇的距离为 $\sqrt{2}$

查看解析
5、已知直线 $l_{1} : 3 x + a y + 1 = 0, l_{2} : (a + 2) x + y + a = 0$ ，（）

A、当 $a = \sqrt{3}$ 时，直线 $l_{1}$ 的倾斜角为 $60^{\circ}$ B、当 $a = - \frac{3}{2}$ 时， $l_{1} ⊥ l_{2}$ C、若 $l_{1}$ $/ /$ $l_{2}$ ，则 $a = - 3$ 或 $a = 1$ D、直线 $l_{2}$ 始终过定点 $(- 1, 2)$

查看解析
6、已知点 $P$ 为椭圆 $\frac{x^{2}}{16} + \frac{y^{2}}{12} = 1$ 上任意一点，直线 $l$ 过 $⊙ M : x^{2} + y^{2} - 4 x + 3 = 0$ 的圆心且与 $⊙ M$ 交于 $A$ ， $B$ 两点，则 $\vec{P A} \cdot \vec{P B}$ 的取值范围是（）

A、 $[3, 35]$ B、 $[2, 34]$ C、 $[2, 36]$ D、 $[4, 36]$

查看解析
7、空间直角坐标系 $O - x y z$ 中，经过点 $P (x_{0}, y_{0}, z_{0})$ 且法向量为 $\vec{m} = (A, B, C)$ 的平面方程为 $A (x - x_{0}) + B (y - y_{0}) + C (z - z_{0}) = 0$ ，经过点 $(x_{0}, y_{0}, z_{0})$ 且一个方向向量为 $\vec{n} = (a, b, c) (a b c \neq 0)$ 的直线 $l$ 的方程为 $\frac{x - x_{0}}{a} = \frac{y - y_{0}}{b} = \frac{z - z_{0}}{c}$ ，阅读上面的材料并解决下列问题：现给出平面 $α$ 的方程为 $2 x - 3 y - z = 0$ ，经过点 $(0, 0, 0)$ 的直线 $l$ 的方程为 $\frac{x}{- 1} = \frac{y}{2} = \frac{z}{- 3}$ ，则直线 $l$ 与平面 $α$ 所成角的正弦值为（）

A、 $\frac{5}{14}$ B、 $\frac{3}{14}$ C、 $\frac{5}{13}$ D、 $\frac{3}{13}$

查看解析
8、如图是某抛物线形拱桥的示意图，当水面处于 $l$ 位置时，拱顶离水面的高度为2.5m，水面宽度为8m，当水面上涨0.9m后，水面的宽度为（）

A、6.4m B、6m C、3.2m D、3m

查看解析
9、圆 $C_{1} : {(x - 2)}^{2} + {(y - 4)}^{2} = 9$ 与圆 $C_{2} : x^{2} + y^{2} - 10 x + 9 = 0$ 的公切条数为（）

A、1条 B、2条 C、3条 D、4条

查看解析
10、已知 $△ A B C$ 三个顶点的坐标分别为 $A (3, - 1)$ ， $B (- 5, 2)$ ， $C (7, 4)$ ，则 $B C$ 边上的中线所在直线的方程为（）

A、 $x + 2 y - 1 = 0$ B、 $2 x + y - 5 = 0$ C、 $2 x - y - 7 = 0$ D、 $x - 2 y - 5 = 0$

查看解析
11、已知 $\vec{a} = (- 3, 2, 5), \vec{b} = (1, 5, - 1)$ ，则 $|\vec{a} - \vec{b}| =$ （）

A、 $\sqrt{57}$ B、 $\sqrt{59}$ C、 $\sqrt{61}$ D、 $3 \sqrt{7}$

查看解析
12、已知抛物线 $y^{2} = 12 x$ 的焦点为 $F$ ，点 $P$ 在抛物线上，定点 $Q (5, 2)$ ，则 $| P Q | + | P F |$ 的最小值为（）

A、6 B、7 C、8 D、9

查看解析
13、在四棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A A_{1} ⊥$ 平面 $A B C D$ ， $A B ⊥ A D$ ， $A B = A D = 2 A A_{1} = 2$ ， $\vec{A E} = λ \vec{A B_{1}}$ ， $\vec{A_{1} F} = μ \vec{A_{1} D}$ ，其中 $λ \in [0, 1]$ ， $μ \in [0, 1]$ .若 $E F$ 与底面 $A B C D$ 所成角的正弦值为 $\frac{\sqrt{5}}{5}$ ，则 $λ μ$ 的最大值是.

查看解析
14、小洪从某公司购进6袋白糖，每袋白糖的标准质量是500g，为了了解这些白糖的质量情况，称出各袋白糖的质量（单位：g）为495，500，500，495，510，500，则这6袋白糖的平均质量为g，这6袋白糖质量的标准差为g.

查看解析
15、抛物线 $x - \frac{1}{16} y^{2} = 0$ 的焦点坐标为，准线方程为.

查看解析
16、如果函数 $y = f (x)$ 满足以下两个条件，我们就称函数 $y = f (x)$ 为 $U$ 型函数.
①对任意的 $x \in [0, 1]$ ，有 $f (x) \geq 1, f (1) = 3$ ；
②对于任意的 $x, y \in [0, 1]$ ，若 $x + y \leq 1$ ，则 $f (x + y) \geq f (x) + f (y) - 1$ .
求证：

(1)、 $y = 3^{x}$ 是 $U$ 型函数；

(2)、 $U$ 型函数 $y = f (x)$ 在 $[0, 1]$ 上为增函数；

(3)、对于 $U$ 型函数 $y = f (x)$ ，有 $f (\frac{1}{3^{n}}) \leq \frac{2}{3^{n}} + 1$ （ $n$ 为正整数）.

查看解析
17、如图的封闭图形的边缘由抛物线 $Γ$ 和垂直于拋物线对称轴的线段 $A B$ 组成.已知 $A B = 4$ ，拋物线的顶点到线段 $A B$ 所在直线的距离为 $2$ .

(1)、请用数学符号语言表达这个封闭图形的边缘；

(2)、在该封闭图形上截取一个矩形 $C D E F$ ，其中点 $C ､ D$ 在线段 $A B$ 上，点 $E ､ F$ 抛物线 $Γ$ 上.求以矩形 $C D E F$ 为侧面， $C F$ 为母线的圆柱的体积最大值；

(3)、求证：抛物线 $Γ$ 的任何两条相互垂直的切线的交点都在同一条直线上.

查看解析
18、如图所示，正三棱锥 $A - B C D$ 的侧面是边长为2的正三角形.

(1)、求正三棱锥 $A - B C D$ 的体积 $V$ ；

(2)、设 $E ､ F ､ G$ 分别是线段 $A C ､ A D ､ B C$ 的中点.
求证：① $C D / /$ 平面 $E F G$ ；②若平面 $E F G$ 交 $B D$ 于点 $H$ ，则四边形 $E F H G$ 是正方形.

查看解析
19、已知向量 $\vec{a} = (cos \frac{3 x}{2}, sin \frac{3 x}{2}), \vec{b} = (cos \frac{x}{2}, - sin \frac{x}{2})$ ，且 $x \in [0, \frac{π}{2}]$ .

(1)、求 $\vec{a} \cdot \vec{b}$ 及 $|\vec{a} + \vec{b}|$ ；

(2)、记 $f (x) = \vec{a} \cdot \vec{b} - |\vec{a} + \vec{b}|$ ，求函数 $y = f (x)$ 的最小值.

查看解析
20、设函数 $f (x) = x + \frac{4}{x}, x \in (- \infty, 0) \cup (0, + \infty)$ .

(1)、求函数 $y = f (x)$ 的单调区间；

(2)、求不等式 $f (x) < 2 x$ 的解集.

查看解析

上一页 880 881 882 883 884 下一页跳转