版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、已知 $△ A B C$ 的内角 $A ､ B ､ C$ 所对边的长度分别为 $a ､ b ､ c$ .

(1)、若 ${(a + b)}^{2} - c^{2} = 4, C = 60 °$ ，求 $△ A B C$ 的面积；

(2)、若 $\frac{cos C}{c} = \frac{cos A}{3 b - a}$ ，求 $sin C$ 的值.

查看解析
2、如图，在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，点 $E$ 、 $F$ 分别是棱 $A B$ 、 $B C$ 的中点.

(1)、求证： $E F ⊥ B D_{1}$ ；

(2)、求二面角 $B_{1} - E F - B$ 的大小.

查看解析
3、设无穷数列 $\{a_{n}\}$ 的前 $n$ 项和为 $S_{n}$ ，且对任意的正整数 $n, a_{n + 1} = \frac{S_{n}}{a_{n}}$ ，则 $\sum_{i = 1}^{5} a_{2 i} - \sum_{i = 1}^{6} a_{2 i - 1}$ 的值可能为（）

A、 $- 6$ B、0 C、6 D、12

查看解析
4、小李研究数学建模“雨中行”问题，在作出“降雨强度保持不变”､“行走速度保持不变”､“将人体视作一个长方体”等合理假设的前提下，他设了变量：
人的身高
人体宽度
人体厚度
降雨速度
雨滴密度
行走距离
风速
行走速度
$h$
$w$
$d$
$v_{r}$
$p$
$D$
$v_{w}$
$v$
并构建模型如下：
当人迎风行走时，人体总的淋雨量为 $T = \frac{p w D}{v} [d v_{r} + h (v_{w} + v)]$ .
根据模型，小李对“雨中行”作出如下解释：
①若两人结伴迎风行走，则体型较高大魁梧的人淋雨是较大；
②若某人迎风行走，则走得越快淋雨量越小，若背风行走，则走得越慢淋雨量越小；
③若某人迎风行走了 $10$ 秒，则行走距离越长淋雨量越大.
这些解释合理的个数为（）

A、 $0$ B、 $1$ C、 $2$ D、 $3$

查看解析
5、如果 $A ､ B$ 是独立事件， $\bar{A}, \bar{B}$ 分别是 $A ､ B$ 的对立事件，那么以下等式不一定成立的是（）.

A、 $P (A \cap B) = P (A) P (B)$ B、 $P (\bar{A} \cap B) = P (\bar{A}) P (B)$ C、 $P (A \cup B) = P (A) + P (B)$ D、 $P (\bar{A} \cap \bar{B}) = [1 - P (A)] [1 - P (B)]$

查看解析
6、已知实数 $a \neq 0$ ，则“ $a > 2$ ”是“ $\frac{1}{a} < \frac{1}{2}$ ”的（）条件.

A、充分非必要 B、必要非充分 C、充分必要 D、既非充分也非必要

查看解析
7、已知实数 $a > 0$ ， $i$ 是虚数单位，设集合 $A = \{z ∣ z = w + \frac{1}{w}, |w| > 1, w \in C, z \in C\}$ ，集合 $B = \{z ∣ |z - 1 + i| = a, z \in C\}$ ，如果 $B \subseteq A$ ，则 $a$ 的取值范围为.

查看解析
8、中国探月工程又称“嫦娥工程”，是中国航天活动的第三个里程碑.在探月过程中，月球探测器需要进行变轨，即从一条椭圆轨道变到另一条不同的椭圆轨道上.若变轨前后的两条椭圆轨道均以月球中心为一个焦点，变轨后椭圆轨道上的点与月球中心的距离最小值保持不变，而距离最大值扩大为变轨前的4倍，椭圆轨道的离心率扩大为变轨前的2.5倍，则变轨前的椭圆轨道的离心率为.（精确到0.01）

查看解析
9、已知 $f (x) = \{\begin{matrix} x^{\frac{1}{3}}, & 0 \leq x \leq a, \\ {log}_{3} x, & x > a \end{matrix}$ ，其中实数 $a > 0$ .若函数 $y = f (x) - 2$ 有且仅有2个零点，则 $a$ 的取值范围为.

查看解析
10、将一个半径为1的球形石材加工成一个圆柱形摆件，则该圆柱形摆件侧面积的最大值为.

查看解析
11、某次杨浦区高三质量调研数学试卷中的填空题第八题，答对得5分，答错或不答得0分，全区共4000人参加调研，该题的答题正确率是 $60 %$ ，则该次调研中全区同学该题得分的方差为.

查看解析
12、已知一个正四棱锥的每一条棱长都为2，则该四棱锥的体积为.

查看解析
13、已知 $|\vec{a}| = |\vec{b}| = 1$ ，若 $(2 \vec{a} - \vec{b}) ⊥ \vec{b}$ ，则向量 $\vec{a}$ 与 $\vec{b}$ 的夹角的余弦值为.

查看解析
14、已知 $|x + 3| + |x - 5| = 8$ ，则实数 $x$ 的取值范围为.

查看解析
15、已知函数 $y = x^{2} + a x + 1$ 是偶函数，则实数 $a$ 的值为.

查看解析
16、已知集合 $A = \{a, b\}$ ，则 $A$ 的子集个数为.

查看解析
17、设 $f (x)$ 为定义在 $R$ 上的偶函数，如图是函数图象的一部分，当 $0 \leq x < 2$ 时，是线段 $O A$ ；当 $x \geq 2$ 时，图象是顶点为 $P (3, 4)$ ，且过点 $(2, 2)$ 的抛物线的一部分.

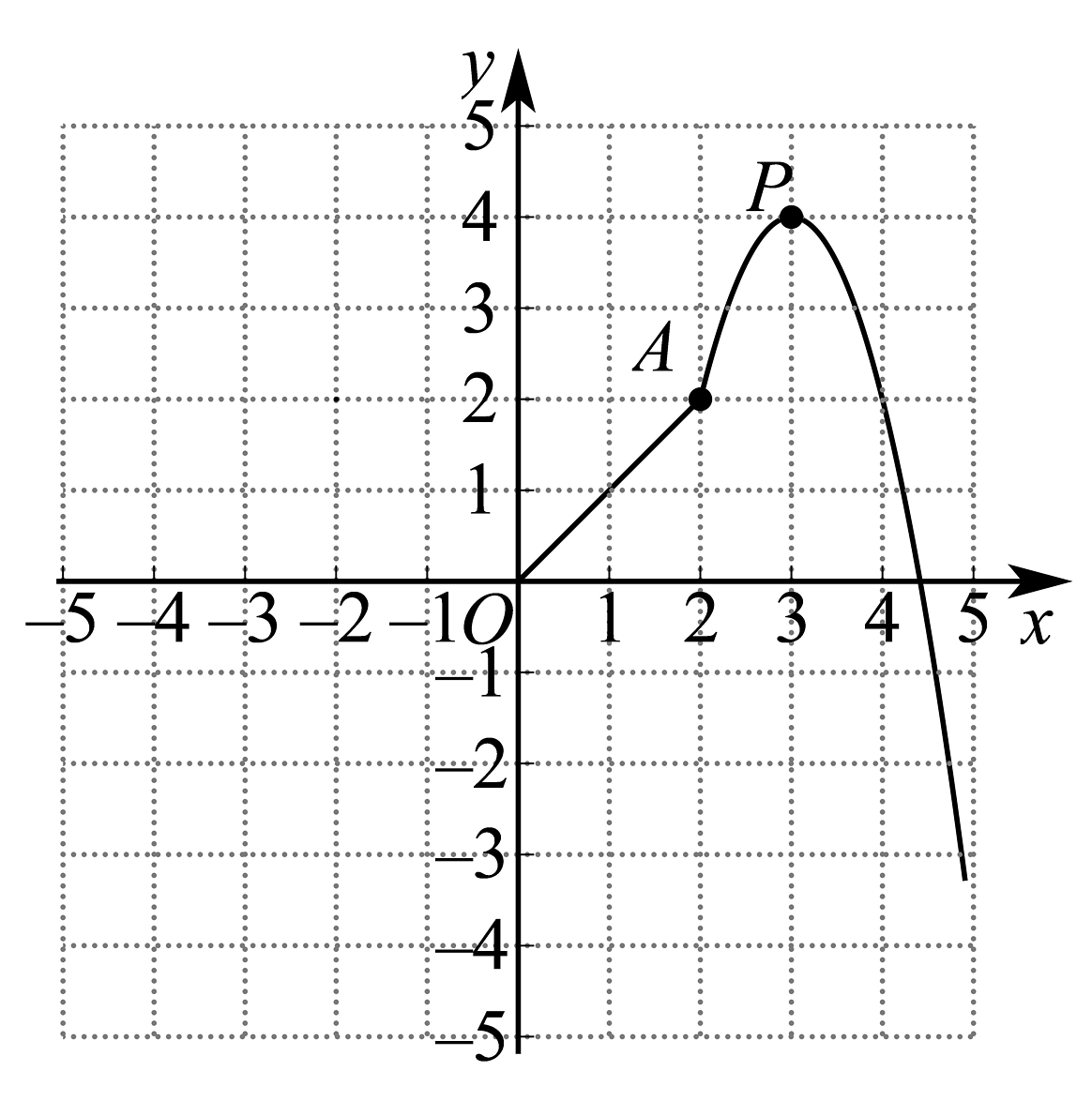(1)、在图中的直角坐标系中画出函数 $f (x)$ 的图象；

(2)、求函数 $f (x)$ 在 $[0, + \infty)$ 上的解析式；

(3)、写出函数 $f (x)$ 的单调区间.

查看解析
18、已知定义域为 $R$ 的函数 $f (x) = \frac{1 - 3^{x}}{b + 3^{x}}$ 是奇函数．

(1)、求 $b$ 的值；

(2)、判断函数 $f (x)$ 在 $R$ 上的单调性，并证明你的结论；

(3)、若 $\exists t \in [0, 6]$ ，使 $f (k - t^{2}) + f (2 t^{2} - 6 t) > 0$ 成立，求实数 $k$ 的取值范围．

查看解析
19、已知各项均为正数的等比数列 $\{a_{n}\}$ 中， $a_{2} + a_{4} = 10, a_{1} a_{5} = 9, a_{1} < a_{5}$ .

(1)、求数列 $\{a_{n}\}$ 的通项公式；

(2)、令 $b_{n} = 3 n a_{n}$ ，求数列 $\{b_{n}\}$ 的前 $n$ 项和 $S_{n}$ .

查看解析
20、已知数列 $\{a_{n}\}$ 为等差数列， $S_{n}$ 为 $\{a_{n}\}$ 的前 $n$ 项和， $a_{3} = 5$ ， $S_{8} = 64$ .

(1)、求数列 $\{a_{n}\}$ 的通项公式；

(2)、设数列 $\{\frac{1}{a_{n} a_{n + 1}}\}$ 的前 $n$ 项和为 $T_{n}$ ，求证： $T_{n} < \frac{1}{2}$ .

查看解析

上一页 800 801 802 803 804 下一页跳转

人的身高	人体宽度	人体厚度	降雨速度	雨滴密度	行走距离	风速	行走速度
$h$	$w$	$d$	$v_{r}$	$p$	$D$	$v_{w}$	$v$