相关试卷
-
1、已知非零向量 , 满足 , 则( )A、 , 的夹角为 B、 C、若 , , 则的外接圆半径长为 D、若 , 向量满足 , 则的最大值是
-
2、若函数的图象关于点对称,在定义域上单调递增,则不等式的解是( )A、 B、 , C、 , D、 ,
-
3、水是生命之源,我国是一个严重缺水的国家,保护水资源是每个公民的义务.在日常生活中淡水需过滤后才能作为饮用水供人们生活使用,假设某工厂在淡水的过滤过程中的各种有害物质的残留数量Y(单位:毫克/升)与过滤时间t(单位:小时)之间的关系满足 , 其中为正常数,为原有害物质数量.该工厂某次过滤淡水时,若前4个小时淡水中的有害物质恰好被过滤掉90%,那么再继续过滤4小时,淡水中有害物质的残留量约为原有害物质的( )A、5% B、3% C、2% D、1%
-
4、的重心为O,过点O的直线与AB,BC所在直线交于点E,F,若 , (),则xy的最小值为( )A、 B、 C、 D、4
-
5、在正方形ABCD中,P是BC的中点,AP与BD交于点Q,则在上的投影向量是( )A、 B、 C、 D、
-
6、已知函数(e为自然对数的底数),且 , 则( )A、2024 B、 C、2022 D、
-
7、已知 , 是不共线的单位向量, , 若 , 则 , 的夹角为( )A、 B、 C、60° D、120°
-
8、已知复数z满足 , 则( )A、 B、 C、 D、
-
9、已知双曲函数 , .(1)、证明:(2)、判断函数的单调性(不用证明),并解关于x的不等式.(3)、若 , 不等式成立,求实数的取值范围.
-
10、已知.(1)、若函数在处取得极值,求实数的值;(2)、若 , 求函数的单调递增区间;(3)、若 , 存在正实数 , 使得成立,求的取值范围.
-
11、已知()在处取得极值.(1)、求实数的值;(2)、求的单调区间;(3)、求在区间上的最大值和最小值.
-
12、已知点 , 点Р是圆C:上的任意一点,线段PA的垂直平分线与直线CP交于点E.(1)、求点E的轨迹方程;(2)、若直线与点E的轨迹有两个不同的交点F和Q,且原点О总在以FQ为直径的圆的内部,求实数m的取值范围.
-
13、已知函数 , 其导函数为 , 则的值为( )A、1 B、2 C、3 D、4
-
14、如图是函数的图象,则下列说法正确的是( )
 A、在上单调递减 B、在上单调递增 C、在区间上的最大值为3,最小值为 D、在上有最大值3,有最小值
A、在上单调递减 B、在上单调递增 C、在区间上的最大值为3,最小值为 D、在上有最大值3,有最小值 -
15、定义:在一个有穷数列的每相邻两项之间插入这两项的和,形成新的数列,我们把这样的操作称为该数列的一次“和扩充”,例如:数列经过第一次“和扩充”后得到数列;第二次“和扩充”后得到数列 . 设数列经过次“和扩充”后得到的数列的项数为 , 所有项的和为 .(1)、若 , 求;(2)、求不等式的解集;(3)、是否存在数列 , 使得数列为等比数列?请说明理由.
-
16、已知双曲线的焦距为8,右焦点为 , 直线与双曲线在一、三象限的交点分别为 , 且 .(1)、求双曲线的方程及的面积;(2)、直线与双曲线交于两点,若直线与轴分别交于点 , 且 . 证明:为定值.
-
17、为增加学生对于篮球运动的兴趣,学校举办趣味投篮比赛,第一轮比赛的规则为:选手需要在距离罚球线1米,2米,3米的三个位置分别投篮一次.在三个位置均投进得10分;在处投进,且在两处至少有一处未投进得7分;其余情况(包括三处均不投进)保底得4分.已知小王在三处的投篮命中率分别为 , 且在三处的投篮相互独立.(1)、设为小王同学在第一轮比赛的得分,求的分布列和期望;(2)、若第二轮比赛中设置两种参赛方法.方法1:按第一轮比赛规则进行比赛;方法2:选手可以选择在处缩短投篮距离0.5米,但得分会减少分.选手可以任选一种规则参加比赛.若小王在处缩短投篮距离0.5米后,投篮命中率会增加 . 请你根据统计知识,帮助小王同学选择采用哪种方法参加比赛更好.
-
18、在三棱柱中,侧面平面 , , 侧面为菱形,且为中点.
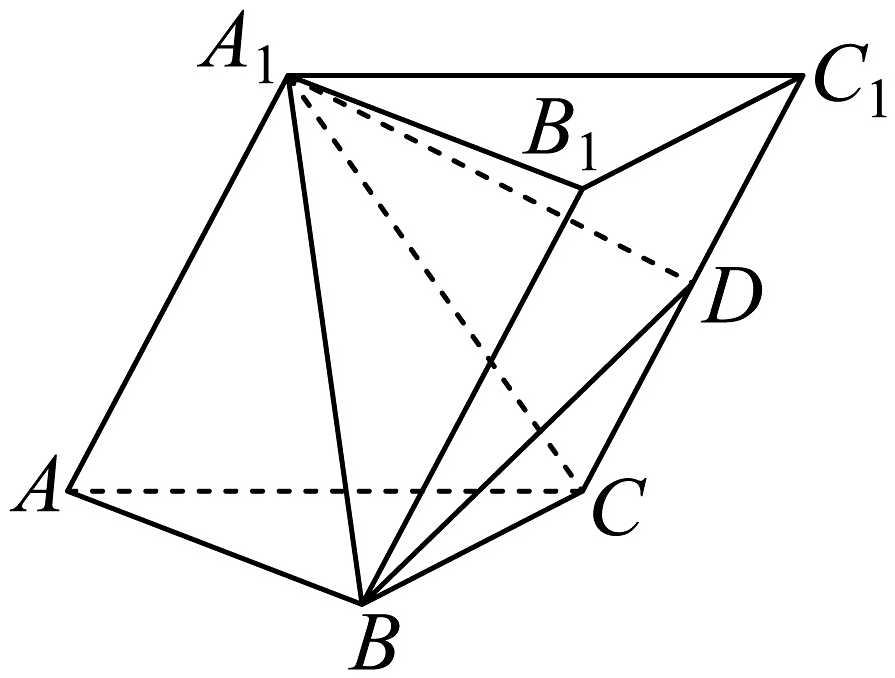 (1)、证明:平面;(2)、求二面角的余弦值.
(1)、证明:平面;(2)、求二面角的余弦值. -
19、已知函数的图象在点处的切线过点 .(1)、求实数的值;(2)、求的单调区间和极值.
-
20、已知抛物线的焦点为 , 直线交抛物线于两点,为抛物线的准线与轴的交点,直线分别交抛物线于两点(点异于点 , ),为坐标原点,则实数的取值范围为; .