相关试卷
-
1、已知 , 那么 .
-
2、已知为上的偶函数, , 为的导函数,且当时, , 则( )A、当时, B、 C、 D、
-
3、根据分类变量x与y的成对样本数据,提出零假设 , 并计算得到 , 则下列说法正确的是( )
0.1
0.05
0.01
0.005
0.001
2.706
3.841
6.635
7.879
10.828
附:
A、零假设为:分类变量x与y独立 B、根据小概率值的独立性检验,可以认为x与y不独立,这个结论犯错误的概率不超过0.1 C、根据小概率值的独立性检验,可以认为x与y不独立,这个结论犯错误的概率不超过0.01 D、若所有样本数据都扩大为原来的10倍,根据小概率值的独立性检验,可以认为x与y不独立,这个结论犯错误的概率不超过0.01 -
4、的展开式中,下列说法正确的是( )A、展开式共有7项 B、常数项为20 C、第二项与第四项的二项式系数相等 D、各项系数之和为0
-
5、已知函数 , 若恒成立,则正整数的最大值为( )A、1 B、2 C、3 D、4
-
6、的展开式中的系数为( )A、495 B、375 C、135 D、15
-
7、如图,一质点在随机外力的作用下,从原点O出发,每次向左或向右移动一个单位长度,向左移动的概率为 , 向右移动的概率为 , 共移动4次,则该质点位于原点右侧的概率为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
8、如图,直线与曲线相切于点P,则函数在上的极值点的个数为( )
 A、3 B、2 C、1 D、0
A、3 B、2 C、1 D、0 -
9、记试验的样本空间 , 事件 , , 则( )A、 B、 C、 D、
-
10、树人中学高二年级举办古诗词比赛,所有同学均可自愿报名参加.某学习小组有6名同学,其中甲、乙两位同学决定要么都去,要么都不去,则该学习小组不同的报名情况总数是( )A、64 B、32 C、31 D、16
-
11、已知随机变量 , 且 , 则( )A、0.3 B、0.4 C、0.5 D、0.6
-
12、对于函数 , 若在定义域内存在实数x,满足 , 则称为“局部奇函数”.(1)、已知二次函数 , , 试判断是否为“局部奇函数”,并说明理由;(2)、若为定义在R上的“局部奇函数”,求函数在的最小值.
-
13、如图,多面体中,底面是菱形, , 四边形是正方形且平面.
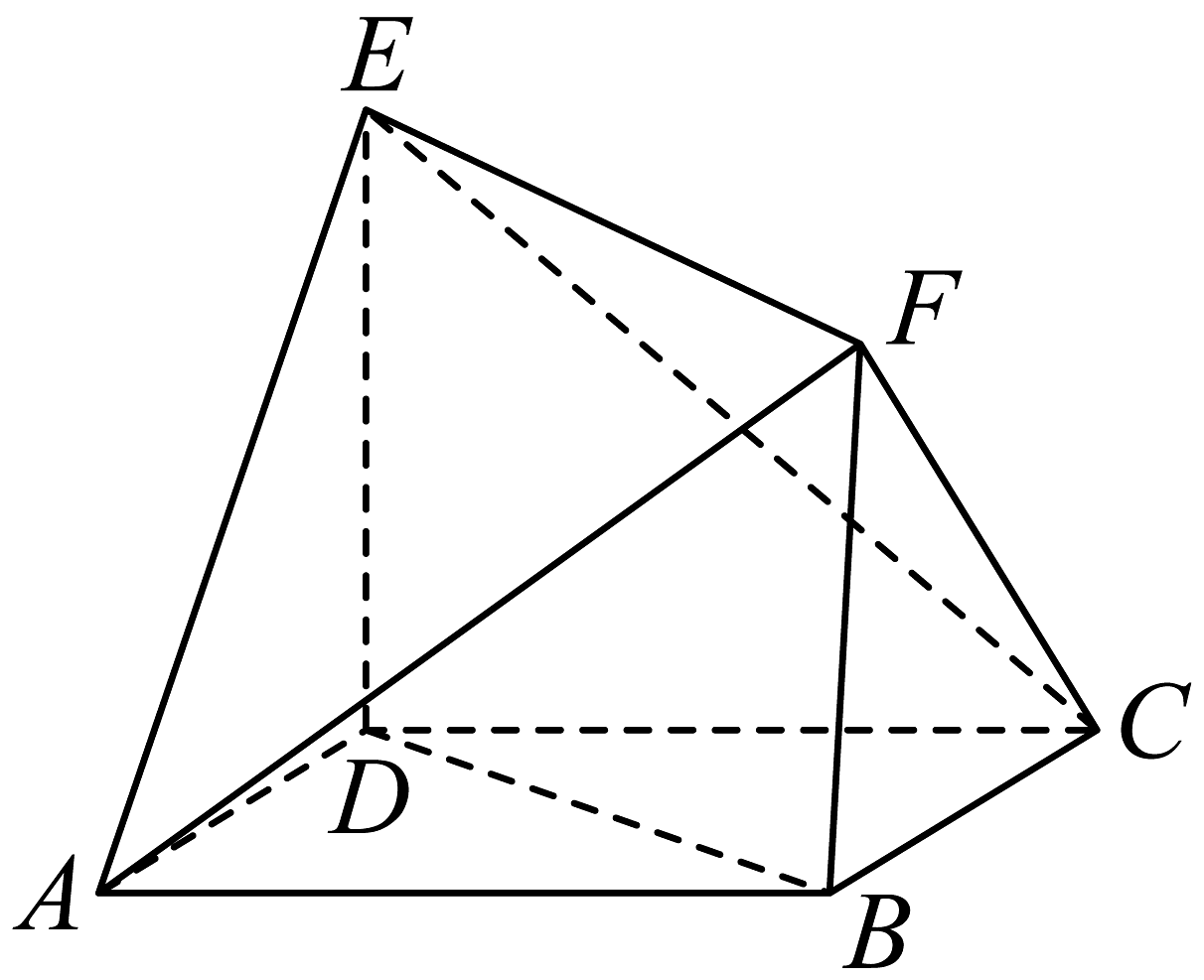
(1)求证:平面;
(2)若 , 求多面体的体积.
-
14、已知空间向量 , .(1)、若与共线,求实数的值;(2)、若与所成角是锐角,求实数的范围.
-
15、已知在中,为平面内一点,则的最小值是.
-
16、将函数的图像向左平移个单位长度,得到函数的图像,下列说法正确的是( )A、当时,为偶函数 B、当时,在区间上单调递增 C、当时,在区间上的值域为 D、当时,函数在区间上有2个零点
-
17、函数的定义域为 , 则的定义域是( )A、 B、 C、 D、
-
18、已知函数 , .(1)、若 , 求曲线在点处的切线方程;(2)、当时,恒成立,求实数的取值范围;(3)、设 , , 若存在 , 使得 . 证明: .
-
19、记等比数列的前n项和为 , 已知.
(1)求数列的通项公式;
(2)令 , 求数列的前n项和.
-
20、如图,在四棱锥中,与均为等腰直角三角形, , E为BC的中点.
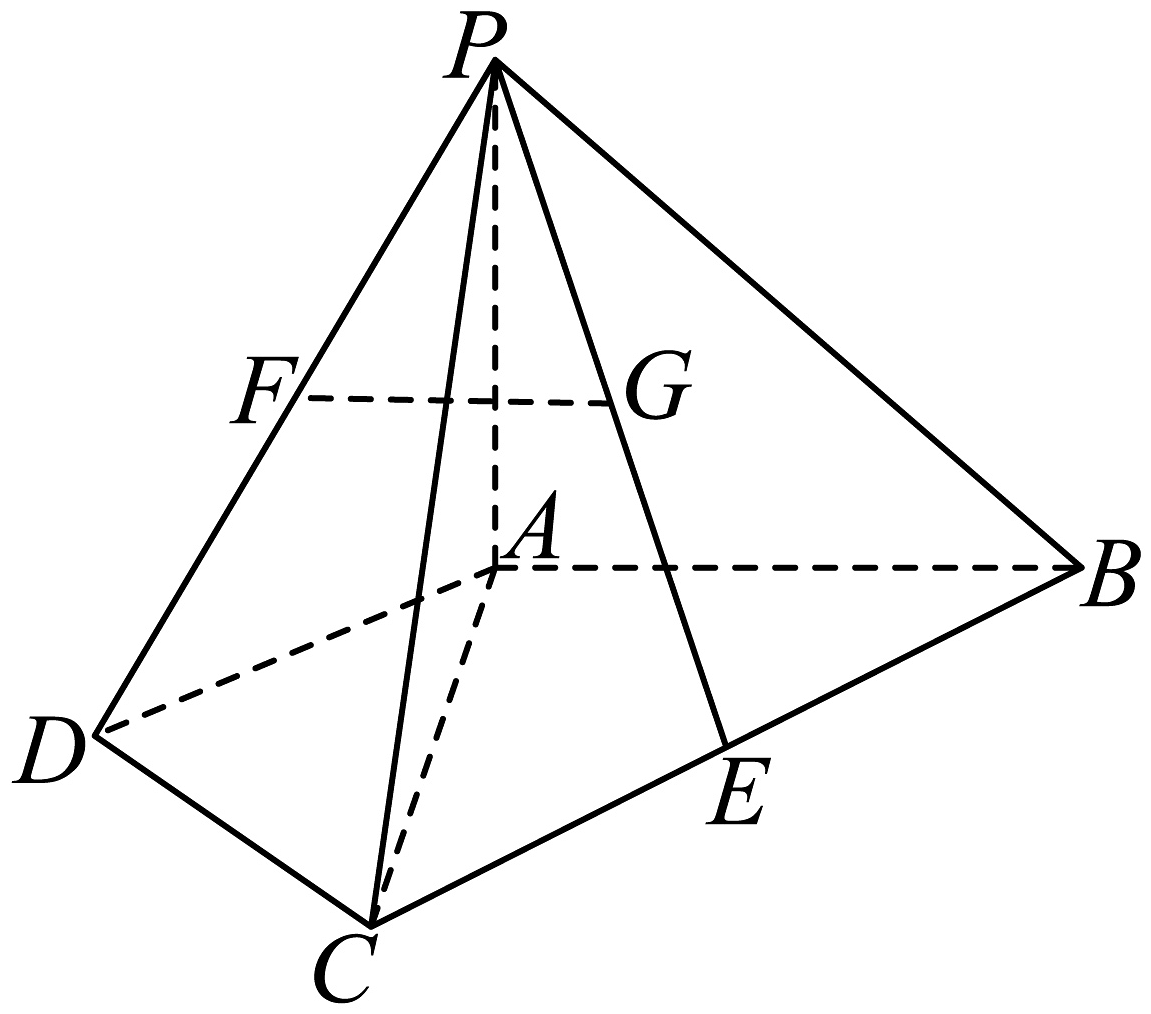 (1)、若分别为的中点,求证:平面PAB;(2)、若平面ABCD, , 求直线AB与平面PCD所成角的正弦值.
(1)、若分别为的中点,求证:平面PAB;(2)、若平面ABCD, , 求直线AB与平面PCD所成角的正弦值.