版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、若向量 $\vec{a} = (- 1, 2), \vec{b} = (m + 1, 2)$ ，且 $(\vec{a} + \vec{b}) ⊥ \vec{a}$ ，则 $m =$ （）

A、 $- 8$ B、8 C、 $- 2$ D、2

查看解析
2、已知：①定积分的定义：
设 $y = f (x)$ 为定义在 $[a, b]$ 上的连续非负函数，为求 $y = f (x) ､ x = a ､ x = b ､ x$ 轴围成的曲边梯形的面积，可采取如下方法：
将区间 $[a, b]$ 分为 $n$ 个小区间，每个小区间长度为 $\frac{b - a}{n}$ ，每个区间即可表示为 $[a + \frac{b - a}{n} (i - 1), a + \frac{b - a}{n} i] (i = 1, 2, 3, \dots n)$ ，再分别过每个区间的左右端点作 $x$ 轴的垂线与 $y = f (x)$ 图象相交，即可得到一个小的曲边梯形.如图，
当 $n \to + \infty$ 时，每个小曲边梯形可近似看作矩形，矩形的宽即为每个小区间的长度，长可由每个小区间内的任一点的函数值近似代替（一般用区间端点的函数值），将这样无穷多个小矩形的面积相加，所得之和即为所求的由 $y = f (x) ､ x = a ､ x = b ､ x$ 轴围成的曲边梯形的面积，即 $S = \lim_{n \to \infty} [\sum_{i = 1}^{n} f (a + \frac{b - a}{n} i) \cdot \frac{b - a}{n}]$ ，上式也记为 $\int_{a}^{b} f (x) d x$ ，即对 $y = f (x)$ 在 $[a, b]$ 上求定积分.
②定积分的计算： $\int_{a}^{b} f (x) d x = F (b) - F (a)$ 其中 $F^{'} (x) = f (x)$ .
根据以上信息，回答以下问题：

(1)、已知 $0 < α < \frac{π}{2}$ ，求证： $\int_{0}^{α} \cos x d x < α$ .

(2)、将 $x = 1 、 x = 2 、 y = \frac{1}{x} 、 x$ 轴围成的图形面积分别表示为定积分的形式与面积和的极限形式，并求其值；

(3)、试证明： $\frac{1}{101} + \frac{1}{102} + \dots + \frac{1}{200} < ln 2 < \frac{1}{100} + \frac{1}{101} + \dots + \frac{1}{199}$ .

查看解析
3、已知数列 $\{a_{n}\}$ 满足 $a_{1} = 1$ ，点 $(a_{n}, a_{n + 1})$ 在直线 $y = 3 x + 1$ 上.

(1)、设 $b_{n} = a_{n} + \frac{1}{2}$ ，证明 $\{b_{n}\}$ 为等比数列：

(2)、求数列 $\{a_{n}\}$ 的前 $n$ 项和 $S_{n}$ ；

(3)、设 $\{\frac{1}{a_{n}}\}$ 的前 $n$ 项和为 $T_{n}$ ，证明： $T_{n} < \frac{3}{2}$ .

查看解析
4、如图，在三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $△ A B_{1} C$ 为正三角形，四边形 $A A_{1} B_{1} B$ 为菱形.

(1)、求证： $A B_{1} ⊥$ 平面 $A_{1} B C$ ；

(2)、若 $A C = B C = 4$ ，且 $A C ⊥ B C, E$ 为 $C C_{1}$ 的中点，求平面 $A B_{1} E$ 与平面 $A B C$ 的夹角的余弦值.

查看解析
5、在 $△ A B C$ 中，角 $A, B, C$ 所对的边分别为 $a, b, c$ .已知 $\frac{1 + tan A}{1 - tan A} = 2 + \sqrt{3}$ .

(1)、求 $∠ A$ ；

(2)、若 $c = 3$ ，且 $△ A B C$ 的面积为 $3 \sqrt{3}$ ，求 $△ A B C$ 的周长.

查看解析
6、已知 $a > 0$ ，函数 $f (x) = |x - \frac{a}{x}| (x > 0)$ .若曲线 $y = f (x)$ 与直线 $y = 2$ 交于 $A, B$ 两点，设 $A, B$ 的横坐标分别为 $x_{1}, x_{2}$ ，写出 $x_{1}, x_{2}$ 与 $a$ 的一个关系式：；分别过点 $A, B$ 作 $x$ 轴的垂线段 $A A_{1}, B B_{1}$ ，垂足分别为 $A_{1}, B_{1}$ ，则四边形 $A A_{1} B_{1} B$ 的面积为.

查看解析
7、已知双曲线 $C : \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0, b > 0)$ 的左､右焦点分别为 $F_{1} 、 F_{2}$ ，若双曲线的左支上一点 $P$ 满足 $\frac{sin ∠ P F_{1} F_{2}}{sin ∠ P F_{2} F_{1}} = 3$ ，以 $F_{2}$ 为圆心的圆与 $F_{1} P$ 的延长线相切于点 $M$ ，且 $\vec{F_{1} M} = 3 \vec{F_{1} P}$ ，则双曲线的离心率为.

查看解析
8、甲､乙､丙三名工人加工同一型号的零件，甲加工的正品率为 $90 %$ ，乙加工的正品率为 $80 %$ ，丙加工的正品率为 $85 %$ ，加工出来的零件混放在一起.已知甲､乙加工的零件数相同，丙加工的零件数占总数的 $40 %$ .现任取一个零件，则它是正品的概率为.

查看解析
9、下列关于函数 $f (x) = x - x ln x$ 的说法，正确的有（）

A、 $x = 1$ 是 $f (x)$ 的极大值点 B、函数 $\dot{f} (x)$ 有两个零点 C、若方程 $f (x) = m$ 有两根 $x_{1}, x_{2}$ ，则 $x_{1} + x_{2} > e$ D、若方程 $f (x) = m$ 有两根 $x_{1}, x_{2}$ ，则 $x_{1} + x_{2} < e$

查看解析
10、下列函数中，对称中心为 $(1, 0)$ 的有（）

A、 $y = sinπ x$ B、 $y = cos (x - 1)$ C、 $y = \frac{1}{2} x - \frac{1}{2}$ D、 $y = x^{3} - 3 x^{2} + x + 1$

查看解析
11、某校举行数学竞赛，现将100名参赛学生的成绩（单位：分）整理如下：
成绩
$[40, 50)$
$[50, 60)$
$[60, 70)$
$[70, 80)$
$[80, 90)$
$[90, 100]$
频数
5
25
30
20
10
10
根据表中数据，下列结论正确的是（）

A、100名学生成绩的极差为60分 B、100名学生成绩的中位数大于70分 C、100名学生成绩的平均数大于60分 D、100名学生中成绩大于60分的人数所占比例超过 $80 %$

查看解析
12、已知平面向量 $\vec{a}, \vec{b}$ 满足 $|\vec{a}| = 1, |\vec{b}| = 2, (\vec{b} - \vec{a}) ⊥ \vec{a}$ ，则 $|\vec{a} + \vec{b}| =$ （）

A、3 B、 $\sqrt{3}$ C、 $\sqrt{7}$ D、1

查看解析
13、设 $z = \frac{2}{i - 1}$ ，则z的共轭复数为（）

A、 $- 1 + i$ B、 $- 1 - i$ C、 $1 + i$ D、 $1 - i$

查看解析
14、已知直线l过点 $(- 3, 4)$ 且方向向量为 $(1, - 2)$ ，则l在x轴上的截距为（）

A、 $- 1$ B、1 C、 $- 5$ D、5

查看解析
15、甲、乙两人参加玩游戏活动，每轮游戏活动由甲、乙各玩一盘，已知甲每盘获胜的概率为 $\frac{3}{4}$ ，乙每盘获胜的概率为 $\frac{2}{3}$ .在每轮游戏活动中，甲和乙获胜与否互不影响，各轮结果也互不影响，则甲、乙两人在两轮玩游戏活动中共获胜3盘的概率为.

查看解析
16、已知集合 $A = \{0, 2, 4, 6\}, B = \{x ∣ 0 < 3^{x} \leq 81\}$ ，则 $A \cap B =$ （）

A、 $\{0, 2, 4\}$ B、 $\{2, 4\}$ C、 $\{2\}$ D、 $\{2, 3, 4\}$

查看解析
17、设椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右顶点分别为 $A_{1}, A_{2}$ ，右焦点 $F (1, 0)$ ， $|A_{2} F| = 1$ ．

(1)、求椭圆方程及其离心率；

(2)、已知点 $P$ 是椭圆上一动点（不与顶点重合），直线 $A_{2} P$ 交 $y$ 轴于点 $Q$ ，若 $△ A_{1} P Q$ 的面积是 $△ A_{2} F P$ 面积的 $2$ 倍，求直线 $A_{2} P$ 的方程．

查看解析
18、半正多面体（semiregular solid）亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，体现了数学的对称美．二十四等边体就是一种半正多面体，是由正方体切截而成的，它由八个正三角形和六个正方形构成（如图所示），若它的所有棱长都为 $\sqrt{2}$ ，则（）

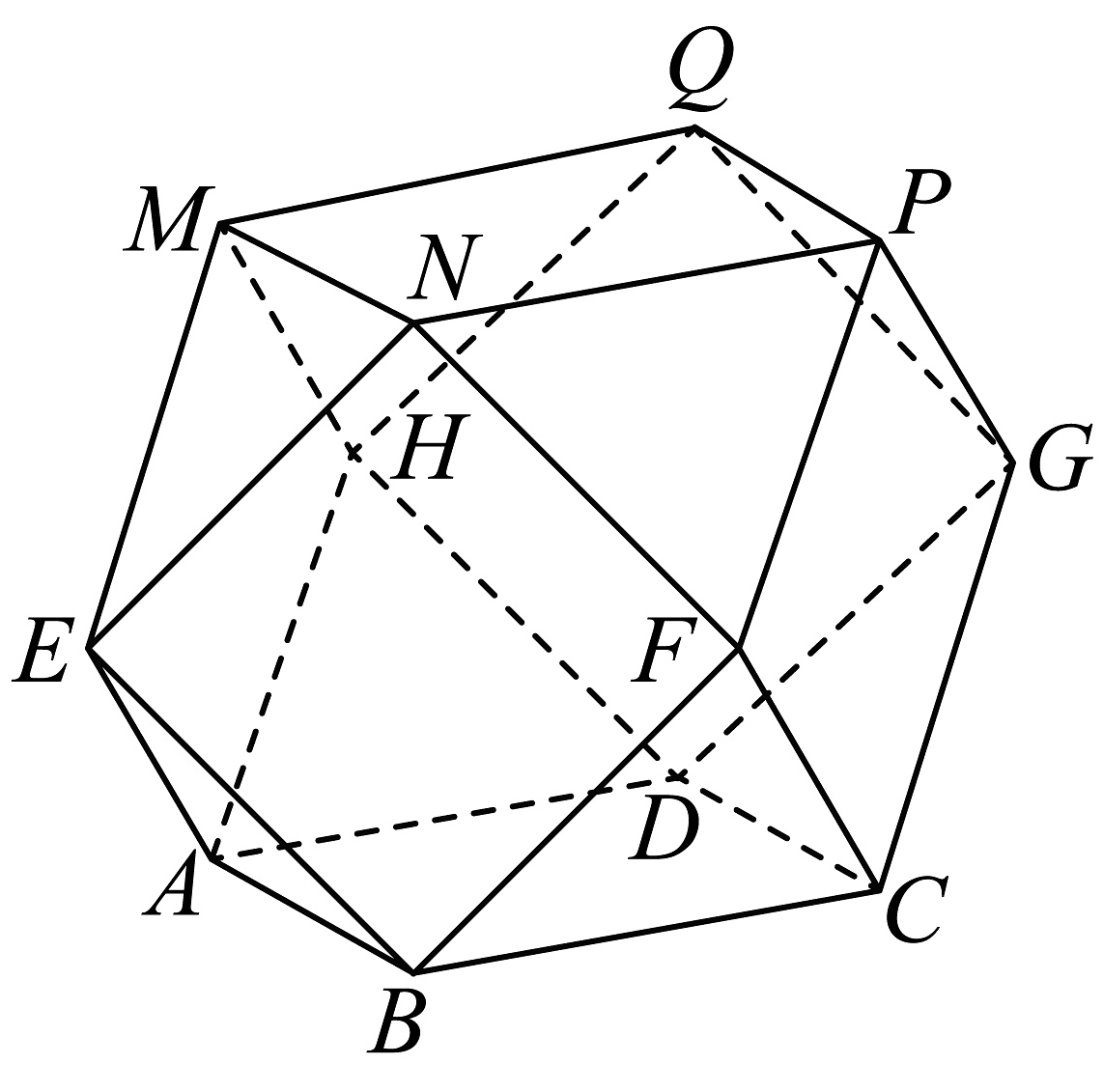A、 $B F ⊥$ 平面EAB B、该二十四等边体的体积为 $\frac{20}{3}$ C、该二十四等边体外接球的表面积为 $6 π$ D、PN与平面EBFN所成角的正弦值为 $\frac{\sqrt{2}}{2}$

查看解析
19、已知曲线 $f (x) = a x^{2} + ln x$ 在点 $(1, f (1))$ 处的切线与 $x$ 轴相交于点 $(\frac{1}{3}, 0)$ ，则实数 $a =$ （）

A、-2 B、-1 C、1 D、2

查看解析
20、已知椭圆 $E : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右顶点为 $A (- 2, 0)$ ， $B (2, 0)$ ，焦距为 $2 \sqrt{3}$ . $O$ 为坐标原点，过点 $O$ 、 $B$ 的圆 $G$ 交直线 $x = 1$ 于 $M$ 、 $N$ 两点，直线 $A M$ 、 $A N$ 分别交椭圆 $E$ 于 $P$ 、 $Q$ .

(1)、求椭圆 $E$ 的方程；

(2)、记直线 $A M$ ， $A N$ 的斜率分别为 $k_{1}$ 、 $k_{2}$ ，求 $k_{1} \cdot k_{2}$ 的值；

(3)、证明：直线 $P Q$ 过定点，并求该定点坐标.

查看解析

上一页 813 814 815 816 817 下一页跳转

成绩	$[40, 50)$	$[50, 60)$	$[60, 70)$	$[70, 80)$	$[80, 90)$	$[90, 100]$
频数	5	25	30	20	10	10