相关试卷
-
1、(1)比较与的大小;
(2)已知 , 求证: .
-
2、若对 , 使得成立,则实数的取值范围为 .
-
3、若命题p:“ , ”是假命题,命题q: , , 是真命题,则实数a的取值范围是 .
-
4、集合的真子集的个数是.
-
5、已知 , 则的最小值为( )A、 B、0 C、1 D、
-
6、设集合含有 , 1两个元素,含有 , 2两个元素,定义集合 , 满足 , 且 , 则中所有元素之积为( )A、 B、 C、8 D、16
-
7、“”是“关于的一元二次方程有实数根”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
8、的定义域为( )A、 B、 C、 D、
-
9、在中, , , , 分别是上的点,满足且经过的重心,将沿折起到的位置,使 , 是的中点,如图所示.
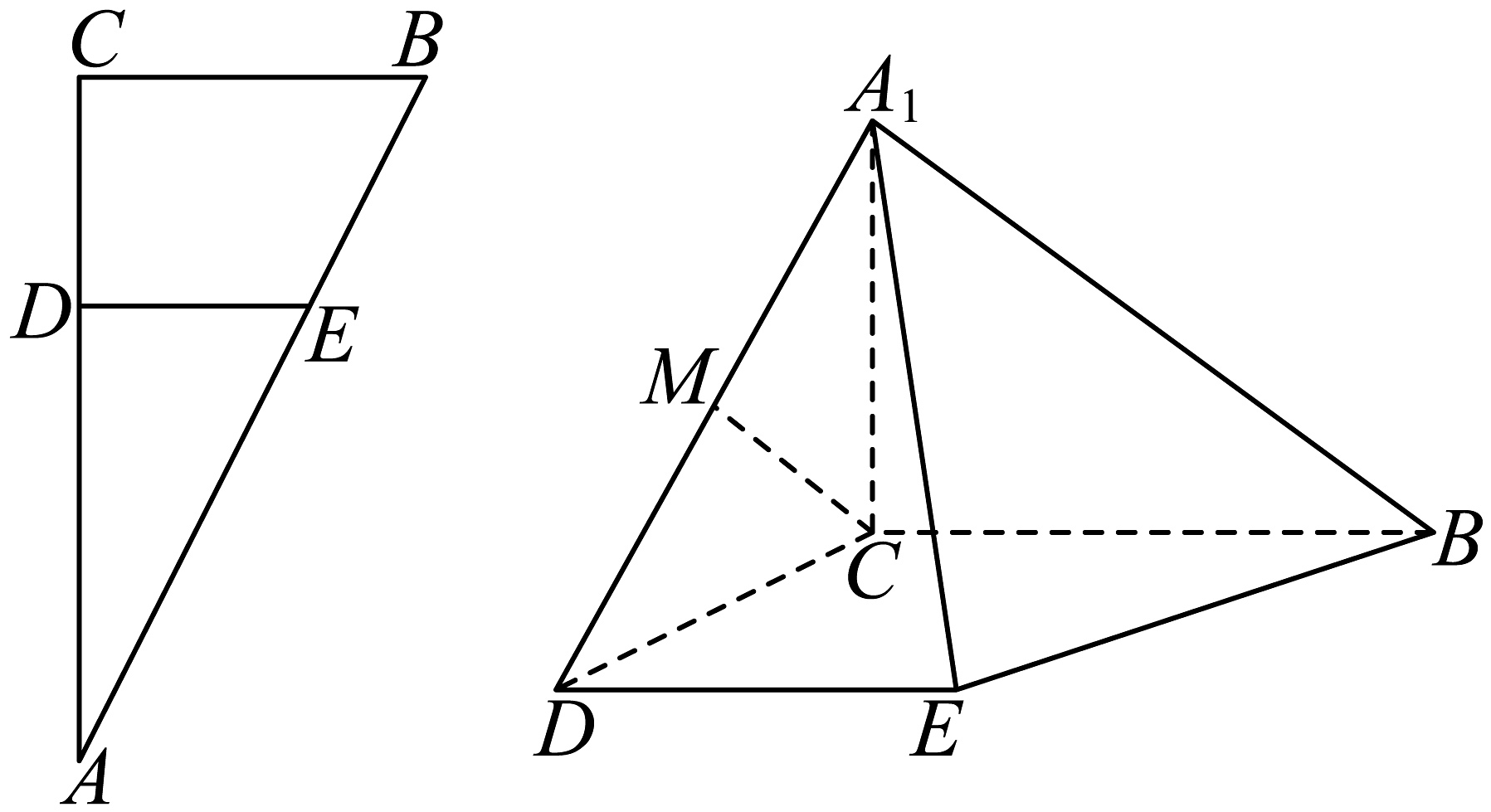 (1)、求证:平面;(2)、求与平面所成角的大小;(3)、在线段上是否存在点 , 使平面与平面成角余弦值为?若存在,求出的长度;若不存在,请说明理由.
(1)、求证:平面;(2)、求与平面所成角的大小;(3)、在线段上是否存在点 , 使平面与平面成角余弦值为?若存在,求出的长度;若不存在,请说明理由. -
10、伯努利试验是在同样的条件下重复地、相互独立地进行的一种随机试验,其特点是每次试验只有两种可能结果.若连续抛掷一枚质地均匀的硬币n次,记录这n次实验的结果,设事件M=“n次实验结果中,既出现正面又出现反面”,事件N=“n次实验结果中,最多只出现一次反面”,则下列结论正确的是( ).A、若 , 则M与N不互斥 B、若 , 则M与N相互独立 C、若 , 则M与N互斥 D、若 , 则M与N相互独立
-
11、已知二次函数满足 , 且该函数的图象经过点 , 在x轴上截得的线段长为4,设.(1)、求的解析式;(2)、求函数在区间上的最小值;(3)、设函数 , 若对于任意 , 总存在 , 使得成立,求a的取值范围.
-
12、如图,在四棱锥中,平面ABCD,PB与底面ABCD所成角为 , 底面ABCD为直角梯形,.
 (1)、求PB与平面PCD所成角的正弦值;(2)、求平面PCD与平面PBA所成角的余弦值;(3)、N为AD中点,线段PC上是否存在动点M(不包括端点),使得点P到平面BMN距离为.
(1)、求PB与平面PCD所成角的正弦值;(2)、求平面PCD与平面PBA所成角的余弦值;(3)、N为AD中点,线段PC上是否存在动点M(不包括端点),使得点P到平面BMN距离为. -
13、已知函数 .(1)、求的最小正周期及单调递增区间;(2)、求在区间上的最值,并求出此时对应的的值;(3)、若在区间上有两个零点,直接写出的取值范围.
-
14、已知等比数列满足 , .
(1)求的通项公式;
(2)从条件①、条件②这两个条件中选择一个作为已知,求数列的前项和 .
条件①:设;
条件②:设 .
-
15、已知函数给出下列四个结论:
①当时,存在最小值;
②当时,存在唯一的零点;
③的零点个数为 , 则函数的值域为;
④当时,对任意 , , .
其中所有正确结论的序号是.
-
16、设函数
①给出一个的值,使得的图像向右平移后得到的函数的图像关于原点对称,;
②若在区间上有且仅有两个零点,则的取值范围是 .
-
17、数列是公差为的等差数列,记的前项和为 , 且成等比数列,则;.
-
18、函数的定义域是 .
-
19、把物体放在冷空气中冷却,如果物体原来的温度是 , 空气的温度是 . 那么后物体的温(单位:℃)可由公式求得,其中k是一个随着物体与空气的接触情况而定的常数.现有46℃的物体,放在10℃的空气中冷却,以后物体的温度是38℃,则k的值约为( )A、0.25 B、 C、0.89 D、
-
20、设 , 则( )A、 B、 C、 D、