相关试卷
-
1、已知集合.(1)、集合 , 且中的任意三个不同的元素 , , 都有.
(i)当时,写出一个满足条件的恰有四个元素的集合;
(ii)对于任意给定的 , 求集合中的元素个数的最大值.
(2)、已知集合P={C|CA}, , 且同时满足以下条件:① , , 都有(其中 , , );② , , 使得(其中).求集合中的元素个数. -
2、如图,在三棱柱中,平面平面 , 平面.
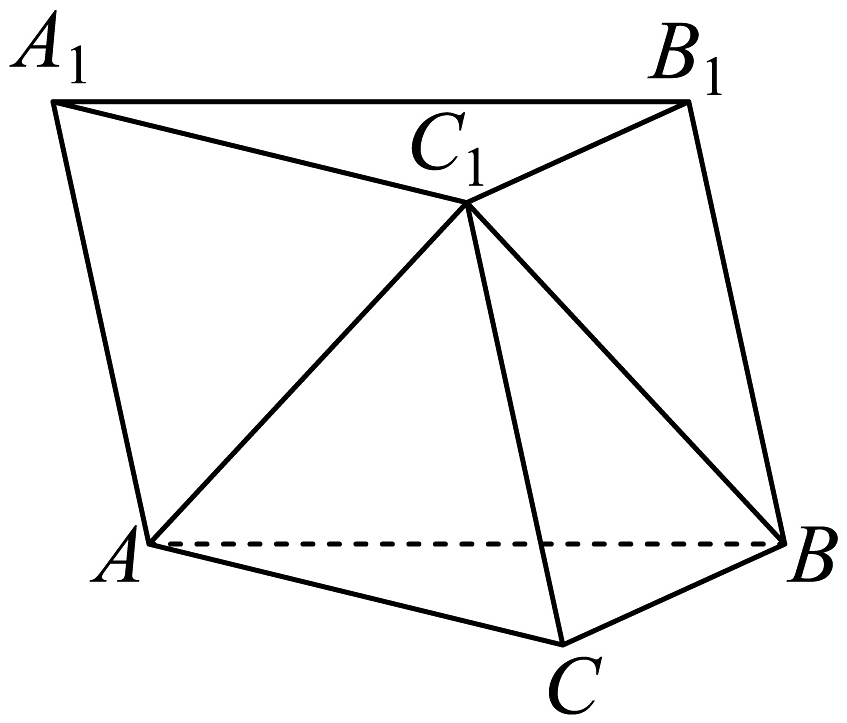 (1)、求证:;(2)、若二面角的正弦值为 , 且 , 求.
(1)、求证:;(2)、若二面角的正弦值为 , 且 , 求. -
3、如图所示的五面体为《九章算术》中记载的羡除,它指的是墓道或隧道.其中 , 四边形 , , 均为等腰梯形,平面平面 , , , , 和间的距离为2,和间的距离为4,则该羡除的体积为.

-
4、已知椭圆和双曲线的焦点相同,则.
-
5、已知函数 , 则( )A、 B、当时, C、当时, D、当时,
-
6、已知 , , , , 其中 , 点为平面内一点,记点到 , 的距离分别为 , , 则下列条件中能使点的轨迹为椭圆的是( )A、 B、 C、 D、
-
7、观察下列散点图的分布规律和特点,其中两个变量存在相关关系的有( )A、
 B、
B、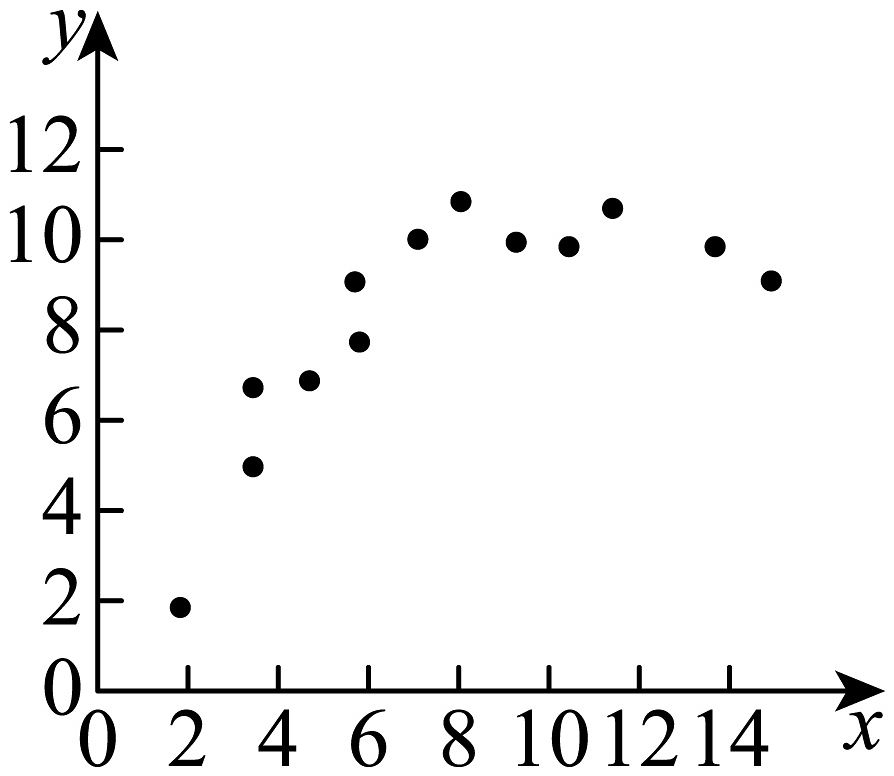 C、
C、 D、
D、
-
8、飞行棋是一种家喻户晓的竞技游戏,玩家根据骰子(骰子为均匀的正六面体)正面朝上的点数确定飞机往前走的步数,刚好走到终点处算“到达”,如果玩家投掷的骰子点数超出到达终点所需的步数,则飞机须往回走超出点数对应的步数.在一次游戏中,飞机距终点只剩3步(如图所示),设该玩家到达终点时投掷骰子的次数为 , 则( )
 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6 -
9、已知函数的值域为 , 则实数的取值范围为( )A、 B、 C、 D、
-
10、已知 , , 则( )A、 B、5 C、 D、
-
11、如图,在矩形中, , 取中点 , 将和分别沿直线 , 折叠,使 , 两点重合于点得到三棱锥 .
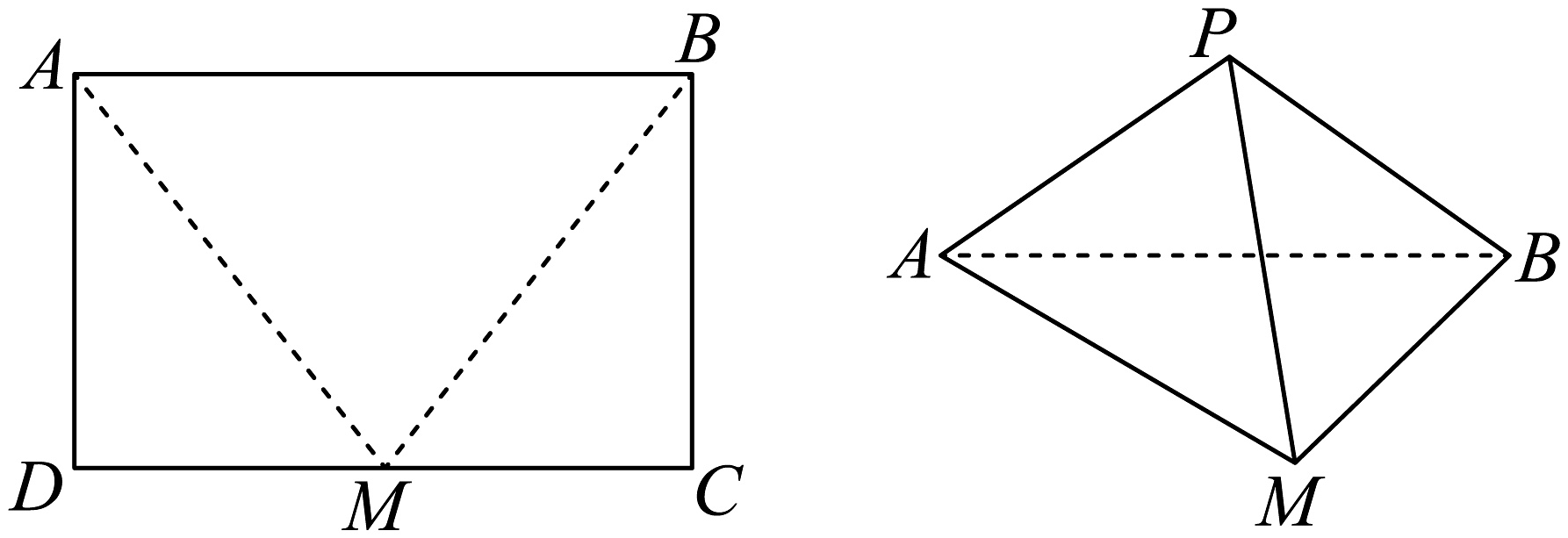 (1)、当时,求证:;(2)、若二面角的平面角为 , 是否存在上一点 , 使得与平面所成角的正弦值为?若存在,请求出点的位置;若不存在,请说明理由.
(1)、当时,求证:;(2)、若二面角的平面角为 , 是否存在上一点 , 使得与平面所成角的正弦值为?若存在,请求出点的位置;若不存在,请说明理由. -
12、如图,在棱长为的正方体中, , 分别是 , 的中点,为上一点.
 (1)、求证:;(2)、求点到平面的距离;(3)、当为何值时,平面与平面所成的夹角的余弦值为.
(1)、求证:;(2)、求点到平面的距离;(3)、当为何值时,平面与平面所成的夹角的余弦值为. -
13、已知圆经过点 , 且圆心为 .(1)、求圆的标准方程;(2)、直线经过点 , 且与圆相交所得弦长为 , 求直线的方程;(3)、求与圆关于直线对称的圆的一般方程.
-
14、已知的三个顶点为.
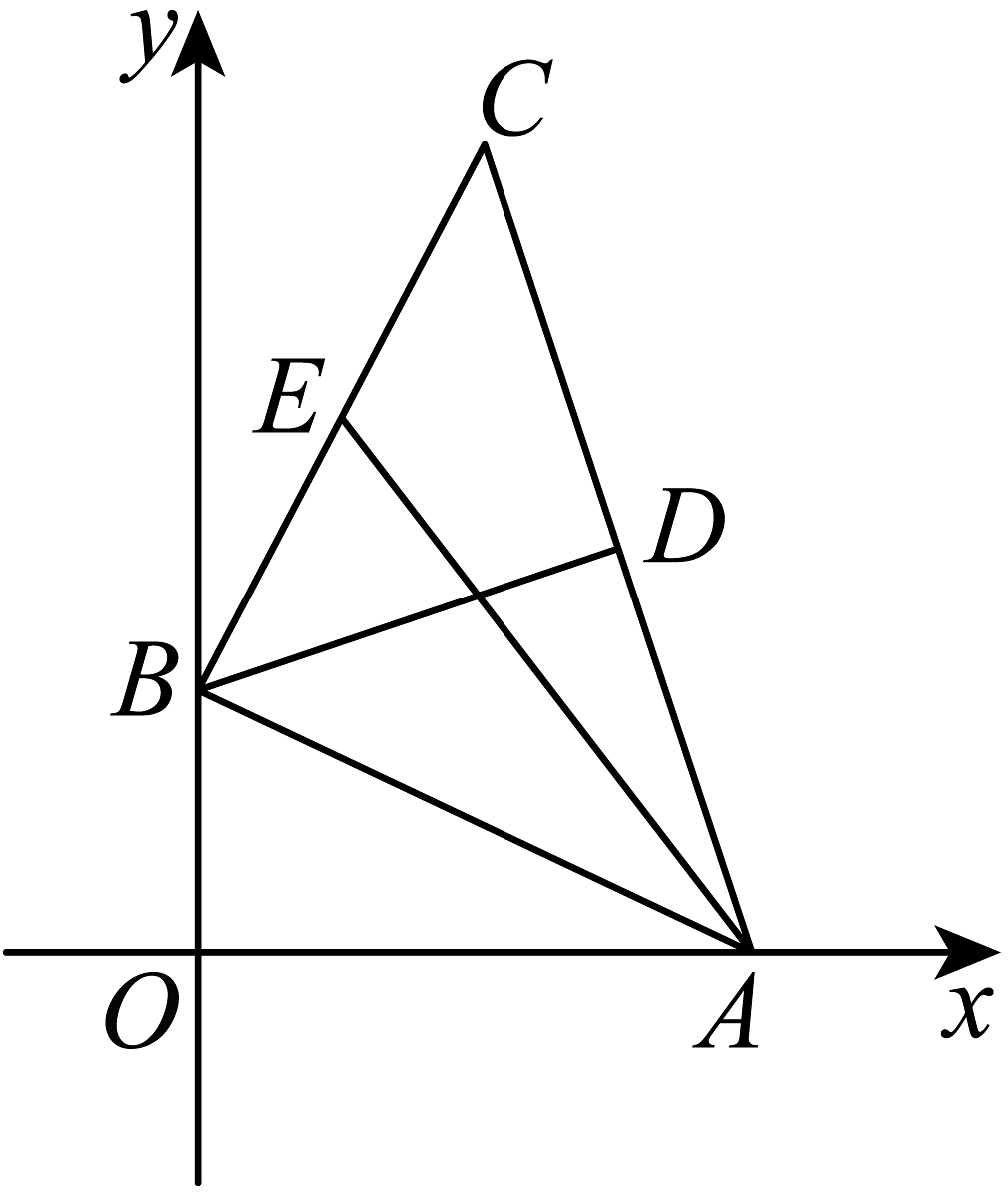 (1)、求边上的高所在直线的方程;(2)、求边上的中线所在直线的方程;(3)、求三角形的面积.
(1)、求边上的高所在直线的方程;(2)、求边上的中线所在直线的方程;(3)、求三角形的面积. -
15、已知正四面体的棱长为 , , 分别为棱 , 的中点,点为线段的中点.
 (1)、用 , , 表示;(2)、求的值;
(1)、用 , , 表示;(2)、求的值; -
16、如图,在直三棱柱中, , , . 以A为原点,建立如图所示空间直角坐标系.
 (1)、求平面的一个法向量.(2)、求直线与平面所成的线面角的正弦值;
(1)、求平面的一个法向量.(2)、求直线与平面所成的线面角的正弦值; -
17、著名数学家华罗庚曾说过“数无形时少直觉,形少数时难人微”,事实上,很多代数问题都可以转化为几何问题加以解决,如:可以转化为平面上点与点之间的距离,结合.上述观点,可得的最小值为 .
-
18、直线l的方向向量为 , 且l过点 , 则点到l的距离为.
-
19、已知直线的方程为 , 那么此直线在轴上的截距为 .
-
20、已知曲线 , 点在曲线上,则下列结论正确的是( )A、当时, B、当时,曲线为圆心为 , 半径为圆的一部分 C、曲线有4条对称轴,且围成的图形面积为 D、当点在第四象限,的最大值是1