版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、已知点 $P$ 为双曲线C： $\frac{x^{2}}{4} - y^{2} = 1$ 上的任意一点，过点 $P$ 作渐近线的垂线，垂足分别为 $E$ ， $F$ ，则（）

A、 $|P E| + |P F| = \frac{4 \sqrt{5}}{5}$ B、 $|P E| \cdot |P F| = \frac{4}{5}$ C、 $\vec{P E} \cdot \vec{P F} = - \frac{12}{25}$ D、 $S_{△ P E F}$ 为定值 $\frac{8}{25}$

查看解析
2、已知10个样本数据，若去掉其中最大和最小的数据，设剩下的8个样本数据的方差为 $s_{1}^{2}$ ，平均数 $\bar{x_{1}}$ ；最大和最小两个数据的方差为 $s_{2}^{2}$ ，平均数 $\bar{x_{2}}$ ；原样本数据的方差为 $S^{2}$ ，平均数 $\bar{x}$ ，若 $\bar{x_{1}} = \bar{x_{2}}$ ，则（）

A、剩下的8个样本数据与原样本数据的中位数不变 B、 $\bar{x} = {\bar{x}}_{1}$ C、剩下8个数据的下四分位数大于原样本数据的下四分位数 D、 $S^{2} = \frac{4}{5} s_{1}^{2} + \frac{1}{5} s_{2}^{2}$

查看解析
3、记函数 $f (x) = cos (ω x + φ) (ω > 0, 0 < φ < π)$ 的最小正周期为 $T$ ，若 $f (T) = - \frac{1}{2}$ ，且 $x = \frac{π}{2}$ 为 $f (x)$ 的一条对称轴，则 $ω$ 的最小值为（）

A、 $\frac{2}{3}$ B、 $\frac{4}{3}$ C、 $\frac{8}{3}$ D、 $\frac{10}{3}$

查看解析
4、上、下底面均为等边三角形的三棱台的所有顶点都在同一球面上，若三棱台的高为3，上、下底面边长分别为 $\sqrt{15}$ ， $2 \sqrt{6}$ ，则该球的表面积为（）

A、32 $π$ B、36 $π$ C、40 $π$ D、42 $π$

查看解析
5、在数列 $\{a_{n}\}$ 中， $a_{1} = 20$ ，对任意正整数 $n, a_{n + 1} = a_{n} - 3$ ，则数列 $\{a_{n}\}$ 的前 $n$ 项和 $S_{n}$ 的最大值为（）

A、77 B、76 C、75 D、74

查看解析
6、圆 $x^{2} + y^{2} = 9$ 的以 $M (2, 1)$ 为中点的弦所在直线方程为（）

A、 $x + 2 y - 4 = 0$ B、 $x - 2 y = 0$ C、 $2 x - y - 3 = 0$ D、 $2 x + y - 5 = 0$

查看解析
7、已知平面向量 $\vec{a} = (- 1, 2)$ ， $\vec{b} = (3, 4)$ ，则 $\vec{a}$ 在 $\vec{b}$ 上的投影向量为（）

A、 $(\frac{1}{4}, \frac{1}{3})$ B、 $(- \frac{1}{4}, \frac{1}{3})$ C、 $(\frac{3}{5}, \frac{4}{5})$ D、 $(- \frac{3}{5}, - \frac{4}{5})$

查看解析
8、设集合 $A = \{x| |x| < 3\}$ ， $B = \{x| x = 2 k$ ， $k \in Z\}$ ，则 $A \cap B =$ （）

A、 $\{0, 2\}$ B、 $\{- 2, 2\}$ C、 $\{- 2, 0, 2\}$ D、 $\{- 2, - 1, 0, 1, 2\}$

查看解析
9、现有A，B两个不透明盒子，都装有m个红球和m个白球，这些球的大小、形状、质地完全相同．

(1)、若 $m = 3$ ，甲、乙、丙依次从A盒中不放回的摸出一球，设X表示三人摸出的白球个数之和，求X的分布列与数学期望；

(2)、若 $m = 1$ ，从A、B两个盒子中各任取一个球交换放入另一个盒子中， $n (n \in N *)$ 次这样的操作后，记A盒子中红球的个数为 $X_{n}$ ，求：
（i） $X_{2} = 1$ 的概率；
（ii） $X_{n}$ 的分布列．

查看解析
10、在直角坐标系xOy中，动圆M与圆 $C_{1} : x^{2} + 2 x + y^{2} = 0$ 外切，同时与圆 $C_{2} : x^{2} - 2 x + y^{2} - 8 = 0$ 内切，记圆心M的轨迹为E．

(1)、求E的方程；

(2)、已知三点T，P，Q在E上，且直线TP与TQ的斜率之积为 $- \frac{3}{4}$ ；
（i）求证：P，O，Q三点共线；
（ii）若 $P Q ⊥ P T$ ，直线TQ交x轴于点A，交y轴于点B，求四边形OPAB面积的最大值．

查看解析
11、已知 $a \geq 0, f (x) = \frac{\ln (1 + a x)}{x}$ ．

(1)、讨论 $f (x)$ 的单调性；

(2)、当n为正整数时，试比较 ${(1 + \frac{1}{n})}^{n}, {(1 + \frac{1}{n + 1})}^{n}, {(1 + \frac{1}{n})}^{n + 1}, {(1 + \frac{1}{n + 1})}^{n + 1}$ 的大小关系，并证明．

查看解析
12、如图，在三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，底面是边长为2的等边三角形， $C C_{1} = 2$ ， $D ， E$ 分别是线段 $A C$ ， $C C_{1}$ 的中点， $C_{1}$ 在平面 $A B C$ 内的射影为 $D$ ．

(1)、求证： $A_{1} C ⊥$ 平面 $B D E$ ；

(2)、若点 $F$ 为线段 $B_{1} C_{1}$ 上的中点，求平面 $B D E$ 与平面 $B D F$ 夹角的余弦值．

查看解析
13、在 $△ A B C$ 中，角A，B，C的对边分别为a、b、c，且 $c \cos B + 2 a \cos A + b \cos C = 0$ ．

(1)、求A；

(2)、如图所示，D为平面上一点，与 $△ A B C$ 构成一个四边形ABDC，且 $∠ B D C = \frac{π}{3}$ ，若 $c = b = 2$ ，求AD的最大值．

查看解析
14、已知函数 $f (x) = \sin (ω x + φ) (ω > 0)$ 在区间 $(\frac{π}{6}, \frac{7 π}{12})$ 上单调，且满足 $f (\frac{π}{6}) = - 1$ ， $f (\frac{3 π}{4}) = 0$ ，则 $ω =$ .

查看解析
15、已知集合 $A = \{a, a + 1\}$ ，集合 $B = \{x \in N | x^{2} - x - 2 \leq 0\}$ ，若 $A \subseteq B$ ，则 $a =$ ．

查看解析
16、下列命题正确的是（）

A、已知变量 $x$ ， $y$ 的线性回归方程 $\hat{y} = 0.3 x - \bar{x}$ ，且 $\bar{y} = 2.8$ ，则 $\bar{x} = - 4$ B、数据4，6，7，7，8，9，11，14，15，19的 $75 %$ 分位数为11 C、已知随机变量 $X ~ B (7, 0.5), P (X = k)$ 最大，则 $k$ 的取值为3或4 D、已知随机变量 $X ~ N (0, 1), P (X \geq 1) = p$ ，则 $P (- 1 < X < 0) = \frac{1}{2} - p$

查看解析
17、已知 $A (x_{1}, y_{1}), B (x_{2}, y_{2})$ 是圆 $x^{2} + y^{2} = 2$ 上两点．若 $x_{1} x_{2} + y_{1} y_{2} = - 1$ ，则 $x_{1} + x_{2} + y_{1} + y_{2}$ 的取值范围是（）

A、 $[- \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}]$ B、 $[- 1, 1]$ C、 $[- \sqrt{2}, \sqrt{2}]$ D、 $[- 2, 2]$

查看解析
18、公元9世纪，阿拉伯计算家哈巴什首先提出正割和余割概念，1551年奥地利数学家、天文学家雷蒂库斯在《三角学准则》中首次用直角三角形的边长之比定义正割和余割，在某直角三角形中，一个锐角的斜边与其邻边的比，叫做该锐角的正割，用sec(角)表示；锐角的斜边与其对边的比，叫做该锐角的余割，用csc(角)表示，则 $\csc 10^{°} - \sqrt{3} \sec 10^{°}$ =（）

A、4 B、8 C、 $\sqrt{3}$ D、 $4 \sqrt{3}$

查看解析
19、 ${(8 - \sqrt{7} x)}^{9}$ 展开式中系数为无理数的项共有（）

A、2项 B、3项 C、4项 D、5项

查看解析
20、在平面直角坐标系 $x O y$ 中，过椭圆 $E :$ $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 中心 $O$ 作斜率为 $\sqrt{2}$ 的一条弦 $A B$ ，将坐标平面沿 $x$ 轴折成一个直二面角.

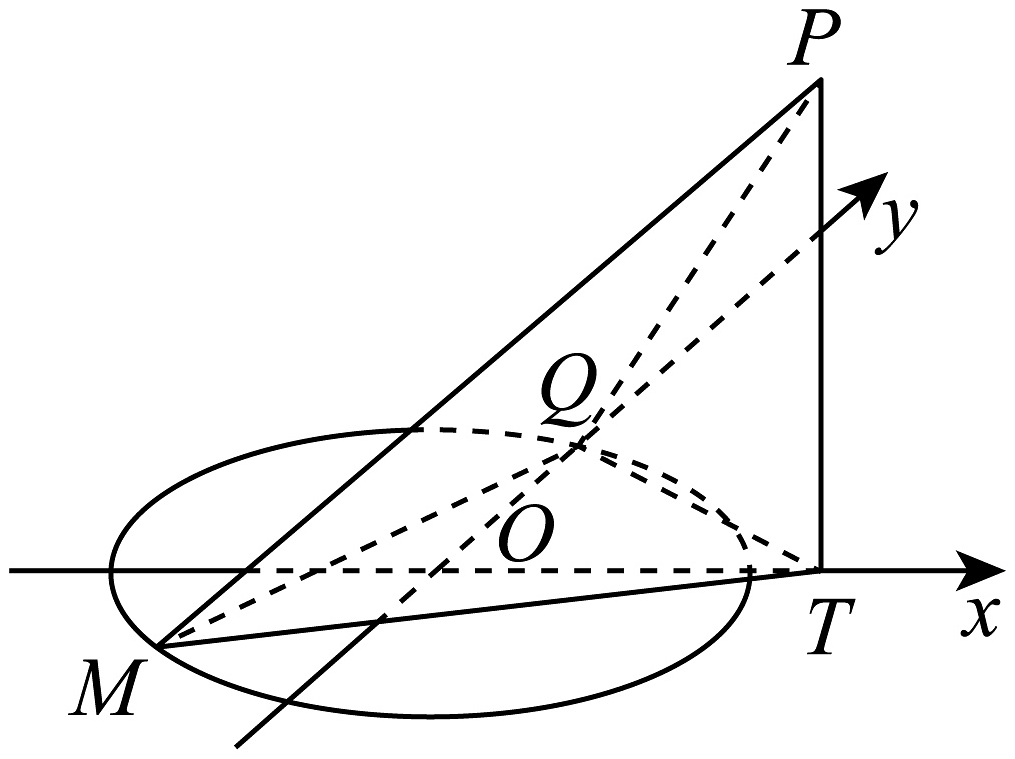(1)、求折起后的连线 $A B$ 与 $x$ 轴所成夹角的大小；

(2)、若此椭圆 $E$ 的离心率为 $\frac{2}{3}$ ，且过点 $Q (0, 1)$ ，求：
（ⅰ）椭圆 $E$ 的标准方程；
（ⅱ）设点 $T (2, 0)$ ，过点 $T$ 作平面 $x O y$ 的垂线 $T P$ ，且 $T P = 2$ ，问：椭圆 $E$ 上是否存在点 $M$ ，使得三角形 $P Q M$ 的面积与三角形 $T Q M$ 的面积之比为最小？若存在，求点 $M$ 坐标；若不存在，请说明理由.

查看解析

上一页 345 346 347 348 349 下一页跳转