相关试卷
-
1、已知全集 , , , 则( )A、 B、 C、 D、
-
2、命题“”的否定为( )A、 B、 C、 D、
-
3、设某公司生产某商品所获利润只由生产成本和销售收入决定.生产成本G(单位:万元)与产量x(单位:百台)的函数关系是;销售收入R(单位:万元)与产量x的函数关系式为 .(1)、将利润(单位:万元)表示为产量x的函数;(利润=销售收入-生产成本)(2)、当产量为何值时,公司所获利润最大?
-
4、已知 , .(1)、求的取值范围;(2)、若 , 求的最小值.
-
5、设全集 , 已知集合 , , .(1)、求;(2)、若 , 求a的取值范围.
-
6、已知函数y=f(x)是定义在(0,+∞)上的减函数,且f(2x-3)>f(5x-6),则实数x的取值范围为 .
-
7、已知定义域为R的函数的图象是连续不断的,且满足以下条件:① , ;② , , 当时,都有;③ , 则下列说法正确的是( )A、函数的图象关于y轴对称; B、; C、若 , 则; D、 , 使得对 , 恒成立.
-
8、已知不等式的解集为 , 下列说法正确的是( )A、; B、 , 2是方程的两个实数根; C、; D、不等式的解集为或 .
-
9、若关于的不等式在上恒成立,则实数的取值范围是( )A、 B、 C、或 D、
-
10、已知幂函数的图像过点 , 则( )A、是奇函数,在上是减函数 B、是偶函数,在上是减函数 C、是奇函数,在上是增函数 D、是偶函数,在上是减函数
-
11、若 , , 则一定有( ).A、 B、 C、 D、
-
12、在下面四个图中,可表示函数的图象的可能是( )
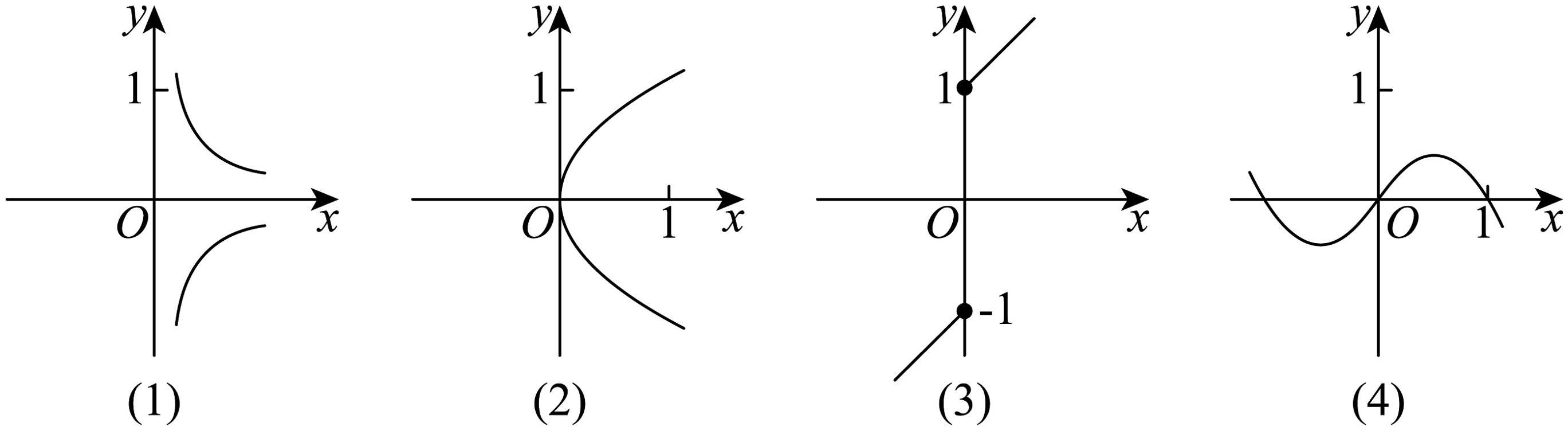 A、(1) B、(2) C、(3) D、(4)
A、(1) B、(2) C、(3) D、(4) -
13、已知正实数、满足 , 则的最小值是( )A、 B、 C、 D、
-
14、已知集合 , 则与集合A的关系为( )A、 B、 C、 D、
-
15、已知函数的图象过点和 .(1)、求函数的解析式;(2)、判断函数在区间上的单调性,并用单调性的定义证明 .
-
16、计算:(1)、;(2)、已知 , 求的值.
-
17、已知函数 , 若 , , 满足 , 记 , 则的取值范围为 .
-
18、已知不等式的解集为 , 则 , 函数的单调递增区间为.
-
19、函数的定义域为 .
-
20、函数在 , 上有定义,若对任意 , , , 有 , 则称在 , 上具有性质 . 设在 , 上具有性质 , 下列命题正确的有A、在 , 上的图象是连续不断的 B、在 , 上具有性质 C、若在处取得最大值1,则 , , D、对任意 , , , , , 有