版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、已知函数 $f (x)$ 的定义域为 $R$ ， $f (x + 1)$ 为奇函数， $f (x + 4) = f (x) + f (1)$ ，则（）

A、 $f (4) = 0$ B、 $f (5) = 0$ C、 $f (6) = 0$ D、 $f (7) = 0$

查看解析
2、已知 $2 a$ ， $a^{2}$ ， $| a |$ ， $2 a + 2$ 的中位数为 $- \frac{1}{2}$ ，则 $a =$ （）

A、 $- 3$ B、 $- 2$ C、 $- 1$ D、1

查看解析
3、若 $\tan α = - 2$ ，则 $\frac{\sin 2 α}{2 \cos^{2} α - \sin^{2} α}$ 的值为（）

A、2 B、 $- 2$ C、 $\frac{2}{3}$ D、 $- \frac{2}{3}$

查看解析
4、已知 $S_{n}$ 是等差数列 $\{a_{n}\}$ 的前 $n$ 项和，若 $a_{1} + a_{6} + a_{11} = 6$ ，则 $S_{9} - S_{2} =$ （）

A、24 B、21 C、14 D、18

查看解析
5、函数 $f (x) = \frac{1}{x} - \log_{2} x - \frac{1}{2}$ 的零点所在区间为（）

A、 $(1, 2)$ B、 $(2, 3)$ C、 $(3, 4)$ D、 $(4, 5)$

查看解析
6、已知集合 $A = {x ∣ - 2 < x < 1}$ ， $B = \{y ∣ y = x^{2} - x\}$ ，则 $A \cap B =$ （）

A、 $[\frac{1}{4}, 1)$ B、 $[- \frac{1}{4}, 1)$ C、 $(- 2, \frac{1}{4}]$ D、 $(- 2, - \frac{1}{4}]$

查看解析
7、 $|i^{3} + i^{2} - i - 1| =$ （）

A、0 B、 $\sqrt{2}$ C、2 D、 $2 \sqrt{2}$

查看解析
8、已知棱长为1的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ ，空间内的动点 $P$ 满足 $\vec{A P} = x \vec{A B} + y \vec{A D} +$ $z \vec{A A_{1}}$ ，其中 $x$ ， $y$ ， $z \in [0, 1]$ ，且 $P$ 到棱 $C C_{1}$ 的距离和 $P$ 到平面 $A B C D$ 的距离相等，则（）

A、当 $z = 1$ 时， $P$ 的轨迹长度为 $\frac{π}{2}$ B、当 $x = \frac{1}{2}$ 时，四面体 $C B C_{1} P$ 的体积为定值 C、存在点 $P$ ，使得 $A P = \frac{π}{4}$ D、直线 $B P$ 与平面 $B C C_{1} B_{1}$ 所成角的正弦值最大为 $\frac{\sqrt{5} - 1}{2}$

查看解析
9、如图，太阳灶是一种将太阳光反射至一点用来加热水或食物的设备，上面装有抛物面形的反光镜，镜的轴截面是抛物线的一部分，已知太阳灶的口径（直径）为4m，深度为0.5m，则该抛物线顶点到焦点的距离为（）

A、0.25m B、0.5m C、1m D、2m

查看解析
10、已知集合 $A = \{1, 2, 3, 4\}, B = \{3, 4, 5, 6\}$ ，则 $A \cap B =$ （）

A、 $\{3, 4\}$ B、 $\{1, 2\}$ C、 $\{5, 6\}$ D、 $\{1, 2, 3, 4, 5, 6\}$

查看解析
11、已知椭圆 $E : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左焦点为 $F$ ，上顶点为 $B$ ，离心率 $e = \frac{\sqrt{2}}{2}$ ，直线FB过点 $P (1, 2)$ .

(1)、求椭圆 $E$ 的标准方程；

(2)、过点 $F$ 的直线 $l$ 与椭圆 $E$ 相交于M，N两点（M、N都不在坐标轴上），若 $∠ M P F = ∠ N P F$ ，求直线 $l$ 的方程.

查看解析
12、某植物园种植一种观赏花卉，这种观赏花卉的高度（单位： $cm$ ）介于 $[15, 25]$ 之间，现对植物园部分该种观赏花卉的高度进行测量，所得数据统计如图所示.

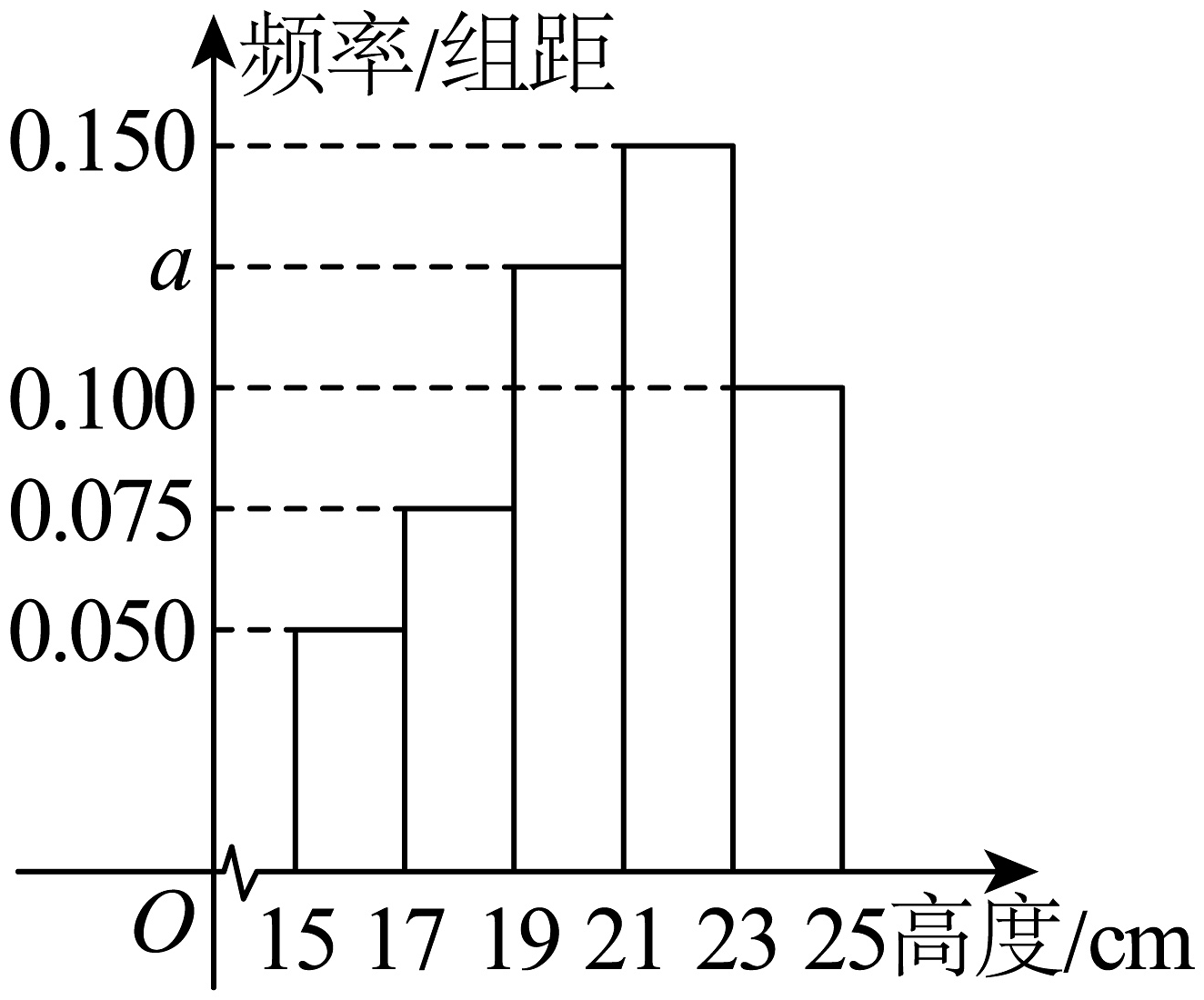(1)、求 $a$ 的值；

(2)、若从高度在 $[15, 17)$ 和 $[17, 19)$ 中分层抽样抽取5株，在这5株中随机抽取3株，记高度在 $[15, 17)$ 内的株数为 $X$ ，求 $X$ 的分布列及数学期望 $E (X)$ ；

(3)、以频率估计概率，若在所有花卉中随机抽取3株，记高度在 $[15, 17)$ 内的株数为 $Y$ ，求 $Y$ 的数学期望.

查看解析
13、如图，在底面 $A B C D$ 是矩形的四棱锥 $P - A B C D$ 中， $A B = 1, B C = 2, P A = P D = \sqrt{6}$ ，点 $P$ 在底面 $A B C D$ 上的射影为点 $O (O$ 与 $B$ 在直线 $A D$ 的两侧 $)$ ，且 $P O = 2$ .

(1)、求证： $A O ⊥ P D$ ；

(2)、求平面 $A B P$ 与平面 $B C P$ 夹角的余弦值.

查看解析
14、已知双曲线C： $\frac{x ^{2}}{a ^{2}} - \frac{y ^{2}}{b ^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点分别为 $F_{1}$ ， $F_{2}$ ， $O$ 为原点，若以 $|F_{1} F_{2}|$ 为直径的圆与 $C$ 的渐近线的一个交点为 $P$ ，且 $|F_{1} P| = \sqrt{3} |O P|$ ，则 $C$ 的离心率为.

查看解析
15、如图，在棱长为2的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $O$ 为正方体的中心， $M$ 为 $D D_{1}$ 的中点， $F$ 为侧面正方形 $A A_{1} D_{1} D$ 内一动点，且满足 $B_{1} F / /$ 平面 $B C_{1} M$ ，则（）

A、三棱锥 $D_{1} - D C B$ 的外接球表面积为 $12 π$ B、动点 $F$ 的轨迹的线段为 $\frac{π}{2}$ C、三棱锥 $F - B C_{1} M$ 的体积为定值 D、若过 $A$ ， $M$ ， $C_{1}$ 三点作正方体的截面 $Ω$ ， $Q$ 为截面 $Ω$ 上一点，则线段 $A_{1} Q$ 长度的取值范围为 $[\frac{2 \sqrt{6}}{3}, 2 \sqrt{2}]$

查看解析
16、已知 $A B$ 是圆O： $x^{2} + y^{2} = 2$ 的直径，M，N是圆O上两点，且 $∠ M O N = 120 °$ ，则 $(\vec{O M} + \vec{O N}) \cdot \vec{A B}$ 的最小值为（）

A、0 B、-2 C、-4 D、 $- 4 \sqrt{3}$

查看解析
17、已知数列 $a_{n} = 2 n - 1,$ $b_{n} = 3 n - 2$ ，则由这两个数列公共项从小到大排列得到的数列为 $\{c_{n}\}$ ，则数列 $\{c_{n}\}$ 的通项公式为（）

A、 $c_{n} = 3 n - 2$ B、 $c_{n} = 4 n - 1$ C、 $c_{n} = 5 n - 3$ D、 $c_{n} = 6 n - 5$

查看解析
18、已知函数 $f (x) = \frac{- 2 x}{x^{2} + 2}$ .

(1)、判断 $f (x)$ 的奇偶性；

(2)、用单调性定义证明 $f (x)$ 在 $(- 1, 1)$ 上单调递减；

(3)、若 $f (x)$ 的定义域为 $(- 1, 1)$ ，解不等式 $f (x^{2}) + f (\frac{1}{6} - \frac{5}{6} x) > 0$ .

查看解析
19、已知函数 $f (x) = 2 \sqrt{3} \sin x \cos x - \cos^{2} x + \sin^{2} x$ ， $x \in R$ ．

(1)、求 $f (x)$ 的单调递增区间；

(2)、当 $x \in [\frac{π}{6}, \frac{5 π}{12}]$ 时，求 $f (x)$ 的最大值和最小值；

(3)、当 $x \in [\frac{π}{6}, \frac{5 π}{12}]$ 时，方程 $f (x) = k$ 恰有两个不同的实数根，求实数k的取值范围．

查看解析
20、摩天轮是一种大型转轮状的机械建筑设施，乘客坐在摩天轮的座舱（挂在轮边缘）里慢慢地往上转，可以从高处俯瞰四周景色.已知某摩天轮的半径为60米，其中心距离地面70米，开启后沿逆时针方向匀速旋转，乘客在座舱转到距离地面最近的位置进舱，转一周大约需要30分钟．

(1)、设乘客P坐上摩天轮的座舱，开始转动t分钟后距离地面高度为h米，求在转动一周的过程中，h关于t的函数解析式；

(2)、摩天轮在转动一圈的过程中，乘客距离地面超过100米的时间有多长？

查看解析

上一页 576 577 578 579 580 下一页跳转