版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、在一个抽奖游戏中，主持人从编号为 $1, 2, 3, 4$ 的四个外观相同的空箱子中随机选择一个，放入一件奖品，再将四个箱子关闭，也就是主持人知道奖品在哪个箱子里，当抽奖人选择了某个箱子后，在箱子打开之前，主持人先随机打开了另一个没有奖品的箱子，并问抽奖人是否愿意更改选择以便增加中奖概率．现在已知甲选择了 $1$ 号箱，用 $A_{i}$ 表示 $i$ 号箱有奖品（ $i = 1, 2, 3, 4$ ），用 $B_{i}$ 表示主持人打开 $i$ 号箱子（ $i = 2, 3, 4$ ），则 $P (B_{3}| A_{1}) =$ ，若抽奖人更改了选择，则其中奖概率为．

查看解析
2、函数 $f (x) = \{\begin{array}{l} a^{x}, x \leq 2 \\ a x^{2} - 13 x + 31, x > 2 \end{array}$ ，其中 $a > 0$ 且 $a \neq 1$ ，若函数是单调函数，则a的一个可能取值为．

查看解析
3、在 $(a x - 1) {(2 x - 1)}^{3}$ 的展开式中，若各项系数的和为 $0$ ，则 $x^{3}$ 的系数为．

查看解析
4、在正四棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A A_{1} = \sqrt{2}$ ， $A B = 1$ ， E，F分别为 $A_{1} B_{1}$ ， $C D$ 的中点，点M是侧面 $A D D_{1} A_{1}$ 上一动点（含边界），则下列结论正确的是（）

A、 $E F$ ∥平面 $A D D_{1} A_{1}$ B、若 $∠ M A_{1} F = ∠ E A_{1} F$ ，则点M的轨迹为抛物线的一部分 C、以 $E F$ 为直径的球面与正四棱柱各棱共有16个公共点 D、以 $E F$ 为直径的球面与正四棱柱各侧面的交线总长度为 $2 \sqrt{2} π$

查看解析
5、已知函数 $f (x) = 2 (cos x + sin x) cos x - 1$ ，则（）

A、 $f (x) \geq f (\frac{5 π}{8})$ B、 $f (1) > f (2)$ C、 $f (\frac{π}{8} + x) + f (\frac{π}{8} - x) = 0$ D、 $\sum_{k = 1}^{2024} f (\frac{k π}{6}) = \sqrt{3}$

查看解析
6、在某次学科期末检测后，从全部考生中选取100名考生的成绩（百分制，均为整数）分成 $[50, 60)$ ， $[60, 70)$ ， $[70, 80)$ ， $[80, 90)$ ， $[90, 100)$ 五组后，得到如下图的频率分布直方图，则（）

A、图中a的值为0.005 B、低于70分的考生人数约为40人 C、考生成绩的平均分约为73分 D、估计考生成绩第80百分位数为83分

查看解析
7、在乎面直角坐标系中，O为坐标原点，已知直线 $l : 2 x + y - 5 = 0$ ，点 $A, B$ 为圆 $x^{2} + y^{2} = 1$ 上两动点，且满足 $∠ A O B = \frac{2 π}{3}$ ，则 $A, B$ 到直线 $l$ 的距离之和的最小值为（）

A、 $2 \sqrt{5} - 2 \sqrt{3}$ B、 $2 \sqrt{5} - 2$ C、 $2 \sqrt{5} - \sqrt{3}$ D、 $2 \sqrt{5} - 1$

查看解析
8、已知斜三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，O为四边形 $A C C_{1} A_{1}$ 对角线的交点，设四棱锥 $O - B C C_{1} B_{1}$ 的体积为 $V_{1}$ ，三棱柱 $A B C - A_{1} B_{1} C_{1}$ 的体积为 $V_{2}$ ，则 $V_{1} : V_{2} =$ （）

A、 $2 : 3$ B、 $1 : 3$ C、 $1 : 4$ D、 $1 : 6$

查看解析
9、设向量 $\vec{a} = (x_{1}, y_{1})$ ， $\vec{b} = (x_{2}, y_{2})$ ，当 $x_{1} \geq x_{2}$ ，且 $y_{1} > y_{2}$ 时，则记作 $\vec{a} ≫ \vec{b}$ ；当 $x_{1} < x_{2}$ ，且 $y_{1} \leq y_{2}$ 时，则记作 $\vec{a} ≪ \vec{b}$ ，有下面四个结论：
①若 $\vec{a} = (2, - 4)$ ， $\vec{b} = (3, 4)$ ，则 $\vec{a} ≪ \vec{b}$ ；
②若 $\vec{a} ≫ \vec{b}$ 且 $λ \vec{a} ≫ μ \vec{b}$ ，则 $λ \geq μ$ ；
③若 $\vec{a} ≫ \vec{b}$ ，则对于任意向量 $\vec{c}$ ，都有 $\vec{a} - \vec{c} ≫ \vec{b} - \vec{c}$ ；
④若 $\vec{a} ≪ \vec{b}$ ，则对于任意向量 $\vec{c}$ ，都有 $\vec{a} \cdot \vec{c} \leq \vec{b} \cdot \vec{c}$ ；
其中所有正确结论的序号为（）

A、①②③ B、②③④ C、①③ D、①④

查看解析
10、已知 $F_{1}$ ， $F_{2}$ 是双曲线C的两个焦点，P为C上一点，且 $cos ∠ F_{1} P F_{2} = \frac{1}{6}$ ， $|P F_{1}| = 3 |P F_{2}|$ ，则C的离心率为（）

A、 $\frac{3}{4}$ B、 $\frac{\sqrt{5}}{2}$ C、 $\frac{3}{2}$ D、3

查看解析
11、已知 $a = {(\frac{1}{2})}^{- 1.1}$ ， $b = 4^{0.6}$ ， $c = {log}_{3} 8$ ，则a，b，c的大小关系为（）

A、 $a < c < b$ B、 $b < c < a$ C、 $c < a < b$ D、 $c < b < a$

查看解析
12、等比数列 $\{a_{n}\}$ 满足 $a_{1} + a_{3} = 10$ ， $a_{2} + a_{4} = 5$ ，则 $a_{5} =$ （）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、1 D、2

查看解析
13、当 $- \frac{1}{2} < m < 2$ 时，复数 $\frac{m + i}{2 + i}$ 在复平面内对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看解析
14、已知集合 $A = \{x |- 3 < x < 4\}$ ， $B = \{x |3 < x < 5\}$ ，则 $\{x | 4 \leq x < 5\} =$ （）

A、 $A \cap (∁_{R} B)$ B、 $∁_{R} (A \cap B)$ C、 $(∁_{R} A) \cup B$ D、 $(∁_{R} A) \cap B$

查看解析
15、为了研究高三年级学生的性别和身高是否大于 $170 cm$ 的关联性，随机调查了某中学部分高三年级的学生，整理得到如下列联表（单位：人)：
性别
身高
合计

低于 $170 cm$
不低于 $170 cm$

女
14
5
19
男
8
10
18
合计
22
15
37

(1)、依据 $α = 0.1$ 的独立性检验，能否认为该中学高三年级学生的性别与身高有关联?

(2)、从身高不低于 $170 cm$ 的15 名学生中随机抽取三名学生，设抽取的三名学生中女生人数为 $X$ ，求 $X$ 的分布列及期望 $E (X)$ .

(3)、若低于 $170 cm$ 的8 名男生身高数据的平均数为 $\bar{x} = 166.5$ ，方差为 $s_{1}^{2} = 9$ ，不低于 $170 cm$ 的10名男生身高数据的平均数为 $\bar{y} = 180$ ，方差为 $s_{2}^{2} = 18$ .请估计该中学男生身高数据的平均数和方差.
附： $χ^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)} ， n = a + b + c + d$ .
$α$
0.1
0.05
0.01
0.005
0.001
$x_{α}$
2.706
3.841
6.635
7.879
10.828

查看解析
16、已知函数 $f (x) = A \sin (ω x + φ)$ （ $ω > 0$ ， $- \frac{π}{2} < φ < \frac{π}{2}$ ）的部分图象如图，则（）

A、 $A = \sqrt{3}$ B、函数 $f (x + \frac{π}{3})$ 的图象关于 $y$ 轴对称 C、函数 $f (x + \frac{π}{3})$ 在 $(0, \frac{π}{4})$ 上单调递减 D、函数 $f (x)$ 在 $(0, 2 π)$ 有4个极值点

查看解析
17、镜面反射法是测量建筑物高度的重要方法，在如图所示的模型中．已知人眼距离地面高度 $h = 1.5 m$ ，某建筑物高 $h_{1} = 4.5 m$ ，将镜子（平面镜）置于平地上，人后退至从镜中能够看到建筑物的位置，测量人与镜子的距离 $a_{1} = 1.2 m$ ，将镜子后移a米，重复前面中的操作，则测量人与镜子的距离 $a_{2} = 3.2 m$ ，则镜子后移距离a为（）

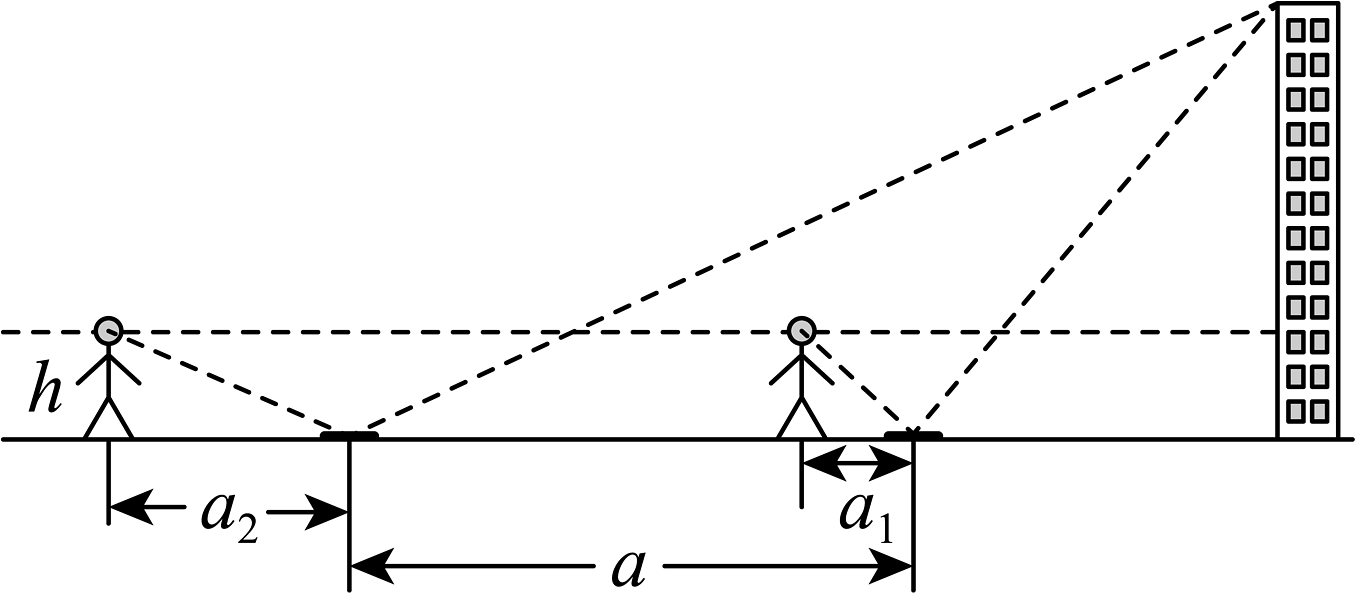A、6m B、5m C、4m D、3m

查看解析
18、如图所示，在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $∠ A C B = 90^{\circ}$ ， $A B = 2$ ， $B C = 1$ ， $A A_{1} = \sqrt{3}$ ．
（1）证明： $A_{1} C$ $⊥$ 平面 $A B_{1} C_{1}$ ；
（2）若 $D$ 是棱 $C C_{1}$ 的中点，在棱 $A B$ 上是否存在一点 $E$ ，使DE∥平面 $A B_{1} C_{1}$ ？证明你的结论．

查看解析
19、如图：在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中 $A B = 2$ ， $M$ 为 $D D_{1}$ 的中点.

(1)、求三棱锥 $M - A B C$ 的体积；

(2)、求证： $B D_{1} / /$ 平面 $A M C$ ；

(3)、若 $N$ 为 $C C_{1}$ 的中点，求证：平面 $A M C / /$ 平面 $B N D_{1}$ .

查看解析
20、如图所示，我国黄海某处的一个圆形海域上有四个小岛，小岛 $B$ 与小岛 $A$ 、小岛 $C$ 相距都为5公里，与小岛 $D$ 相距为 $3 \sqrt{5}$ 公里．已知角 $A$ 为钝角，且 $\sin A = \frac{3}{5}$ ．

(1)、求小岛 $A$ 与小岛 $D$ 之间的距离；

(2)、记 $∠ C D B$ 为 $α$ ， $∠ C B D$ 为 $β$ ，求 $\sin (2 α + β)$ 的值．

查看解析

上一页 411 412 413 414 415 下一页跳转

性别	身高		合计
	低于 $170 cm$	不低于 $170 cm$
女	14	5	19
男	8	10	18
合计	22	15	37

$α$	0.1	0.05	0.01	0.005	0.001
$x_{α}$	2.706	3.841	6.635	7.879	10.828