相关试卷
-
1、已知O为坐标原点,双曲线的离心率为 , 且过点.(1)、求C的标准方程;(2)、过C的右焦点F的直线与双曲线C的左、右两支分别交于两点A、B,点Q是线段的中点,过点F且与垂直的直线交直线于M点,点N满足;
①证明:点M在一条定直线上;
②求四边形面积的最小值.
-
2、在中,角 , , 的对边长分别为 , , , 的面积为 , 且 .
(1)求角的大小;
(2)若 , 且当时,取得最大值 , 试求的值.
-
3、已知函数 ,(1)、若 , 求曲线在点处的切线方程;(2)、讨论函数的单调性;
-
4、袋子中装有大小、形状完全相同的2个白球和2个红球.现从中不放回地摸取2个球,已知第二次摸到的是红球,则第一次摸到红球的概率为.
-
5、已知点是抛物线的焦点, , 是经过点的弦且 , 直线的斜率 , , 两点在轴上方,为坐标原点,则下列结论中正确的是( )A、 B、四边形面积的最小值为 C、 D、若 , 则直线的斜率为
-
6、已知 , , 下列给出的实数的值,能使p是q的充分不必要条件的是( )A、 B、 C、 D、=2025
-
7、已知 , , , 则( )A、 B、 C、 D、
-
8、如图,已知函数 , 点A,B是直线与函数的图象的两个交点,若 , 则函数的单调递减区间为( )
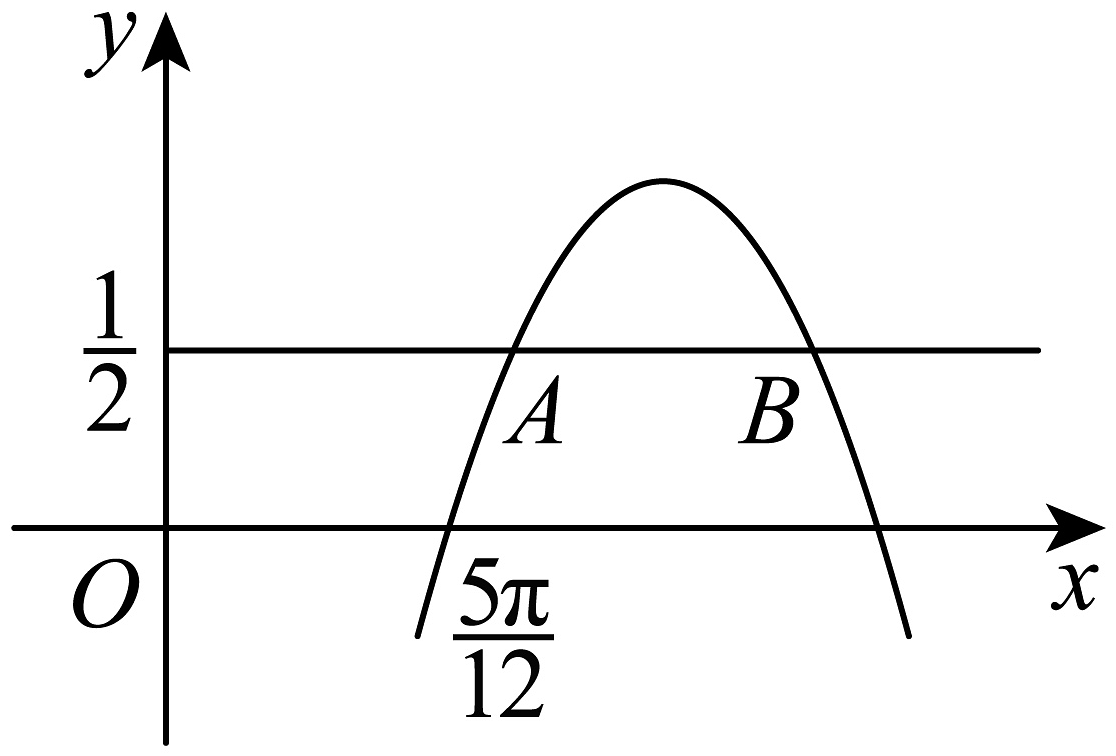 A、 B、 C、 D、
A、 B、 C、 D、 -
9、已知函数是定义在上的奇函数,当时, , 则=A、 B、 C、 D、
-
10、已知 , 则( )A、 B、 C、3 D、
-
11、已知非零向量满足 , 则与的夹角的余弦值是( )A、 B、 C、 D、
-
12、已知集合 , 则( )A、 B、 C、 D、
-
13、已知均为正实数,且满足 .(1)、求的最小值;(2)、求证:.
-
14、在平面直角坐标系中,已知直线(为参数),为的倾斜角,与轴正半轴,轴正半轴分别交于两点,且的面积是 .(1)、求;(2)、以坐标原点为极点,轴正半轴为极轴建立极坐标系,求的极坐标方程.
-
15、已知函数 , 其中 , 设为的极小值点,为的极值点, , 并且 . 将点依次记为A,B,C,D.(1)、求的值;(2)、若四边形为梯形且面积为1,求a,d的值.
-
16、已知点P到圆的切线长与到y轴的距离之比为(1)、求动点P的轨迹C的方程;(2)、设曲线C的两焦点为、 , 试求t的取值范围.使得曲线C上不存在点Q,使.
-
17、某安全生产监督部门对5家小型煤矿进行安全检查(简称安检).若安检不合格,则必须整改.若整改后经复查仍不合格,则强制关闭.设每家煤矿安检是否合格是相互独立的,且每家煤矿整改前安检合格的概率是0.5,整改后安检合格的概率是0.8,计算(结果精确到0.01):(1)、恰好有两家煤矿必须整改的概率;(2)、某煤矿不被关闭的概率;
-
18、如图已知是所在平面的一条斜线,点是在平面上的射影,且在的高上. , 与之间的距离为 , 点 .
 (1)、证明是二面角的平面角;(2)、当时,证明平面;
(1)、证明是二面角的平面角;(2)、当时,证明平面; -
19、(1)已知 , , 分别为三个内角 , , 的对边.请用向量方法证明等式;
(2)若三个正数 , , 满足 , 证明:以 , , 为长度的三边可以构成三角形.
-
20、某种疾病的患病率为 , 通过验血诊断该病的误诊率(将未患病者判定为阳性的概率)为 , 漏诊率(将患病者判定为阴性的概率)为 , 每人的诊断结果互不影响,则若某人验血的诊断结果是阳性,则该人患病的概率为