相关试卷
-
1、在平行四边形中, , , 与交于点 . 设 , , 请用表示;若 , 则 .
-
2、某射击俱乐部开展青少年射击培训,俱乐部共有6支气枪,其中有2支气枪未经试射校正,有4支气枪已校正,若用校正过的气枪射击,射中10环的概率为0.8,用未校正过的气枪射击,射中10环的概率为0.4,某少年射手任取一支气枪进行1次射击,射中10环的概率是;若此少年射手任取一支气枪进行4次射击(每次射击后将气枪放回),每次射击结果相互不影响,则4次射击中恰有2次射中10环的概率为 .
-
3、在的二项展开式中,常数项为 .
-
4、为虚数单位,若复数满足 , 则的虚部为 .
-
5、已知双曲线:的一条渐近线与抛物线:的准线相交于点 , 点的横坐标为 , 双曲线的左、右焦点分别为和 . 若过点的直线交的左支于 , 两点,且(为坐标原点),记点到直线的距离为 , 则( )A、 B、 C、 D、
-
6、在正方体中,是棱上的点,且 . 平面将此正方体分为两部分,设两部分体积分别为和 , 则( )A、 B、 C、 D、
-
7、已知函数的两条相邻对称轴之间的距离为 , 现将图象向右平移后得到函数的图象,若函数在区间上单调递增,则实数的取值范围是( )A、 B、 C、 D、
-
8、设 , , 分别为函数 , , 的零点,则 , , 的大小关系为( )A、 B、 C、 D、
-
9、若直线:与圆:相交于 , 两点,则的最小值为( )A、 B、 C、 D、
-
10、一组数据按从小到大的顺序排列为1,3, , 7,10,11,若该组数据的中位数是这组数据极差的 , 则该组数据的第45百分位数是( )A、3 B、4 C、5 D、7
-
11、已知 , 为两条不同的直线, , 为两个不同的平面,则下列说法中正确的是( )A、若 , , 则 B、若 , , 则 C、若 , , 则 D、若 , , 则
-
12、已知 , 使得不等式“”成立的一个充分不必要条件是( )A、 B、 C、 D、
-
13、已知是圆上一动点,定点 , 线段的垂直平分线与直线交于点 , 记点的轨迹为 .(1)、求的方程;(2)、若直线与曲线恰有一个共点,且与直线 , 分别交于、两点,的面积是否为定值?若是,求出该定值,若不是,请说明理由.
-
14、如图,在正三棱台中, ,
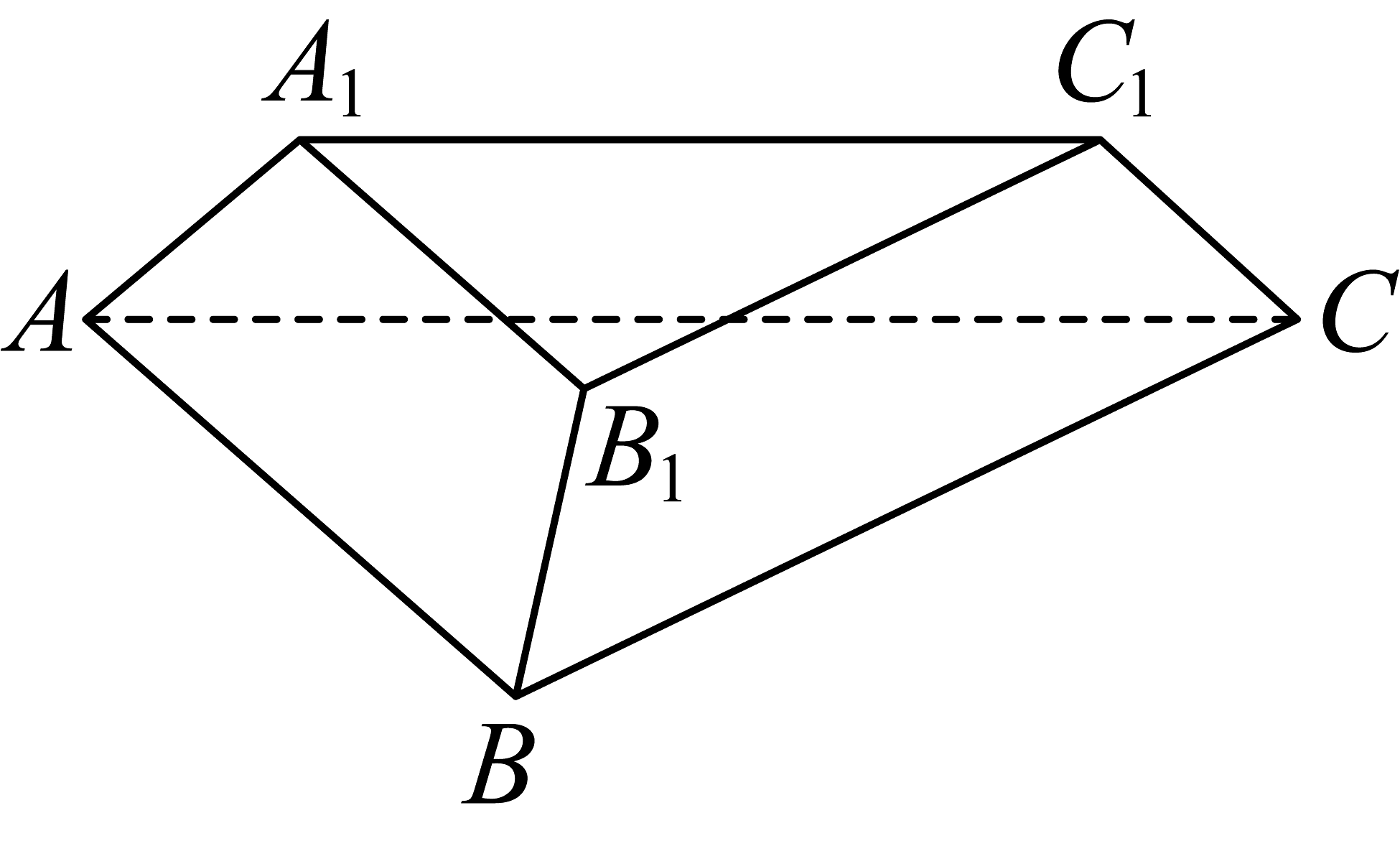 (1)、若 , 证明:平面;(2)、若三棱台的高为 , 求平面与平面夹角的余弦值.
(1)、若 , 证明:平面;(2)、若三棱台的高为 , 求平面与平面夹角的余弦值. -
15、袋中有三个相同的小球,用不同数字对三个小球进行标记.从袋中随机摸出一个小球,接着从袋中取出比该小球上数字大的所有小球不再放回 , 并将该小球放回袋中.然后,对袋中剩下的小球再作一次同样的操作,此时袋中剩下2个小球的概率为.
-
16、如图,长方体中, , 点是半圆弧上的动点(不包括端点),点是半圆弧上的动点(不包括端点),则下列说法正确的是( )
 A、的取值范围是 B、若与平面所成的角为 , 则 C、的最小值为 D、若三棱锥的外接球表面积为 , 则
A、的取值范围是 B、若与平面所成的角为 , 则 C、的最小值为 D、若三棱锥的外接球表面积为 , 则 -
17、已知P为圆上的动点不在坐标轴上 , 过P作轴,垂足为Q,将绕y轴旋转一周,所得几何体的体积最大时,线段OQ的长度为( )A、 B、 C、 D、
-
18、图1是世界上单口半径最大、灵敏度最高的射电望远镜“中国天眼”——口径抛物面射电望远镜,反射面的主体是一个抛物面(抛物线绕其对称轴旋转所形成的曲面称为抛物面),其边缘距离底部的落差约为156.25米,它的一个轴截面开口向上的抛物线C的一部分,放入如图2所示的平面直角坐标系内,已知该抛物线上点P到底部水平线(x轴)距离为 , 则点到该抛物线焦点F的距离为( )

 A、 B、 C、 D、
A、 B、 C、 D、 -
19、函数 的图象大致为( )A、
 B、
B、 C、
C、 D、
D、
-
20、已知实数 , , 满足 , , 则( )A、 B、 C、 D、