-
1、找规律:1,4,9,16, , 36.
-
2、2,4,6,8,10, , 第项为.
-
3、设全集 , 集合 , 若 , 则 .
-
4、集合 , 集合 , 则 .
-
5、数列的前n项和 , 则( )A、140 B、120 C、40 D、50
-
6、某校招聘了6名教师,现平均分配给学校的两个校区,其中2名英语教师不能分配在同一个校区,另外3名数学教师也不能全分配在同一个校区,则不同的分配方案共有( )A、12种 B、14种 C、24种 D、48种
-
7、在中,满足 , 则( )A、60° B、60°或120° C、30°或150° D、120°
-
8、计算:( )A、 B、 C、 D、
-
9、化简:( )A、 B、 C、 D、
-
10、2022年7月19日,亚洲奥林匹克理事会宣布杭州亚运会定于2023年9月23日至10月8日举行,用标记亚运会开始的日期,即 , 用表示亚运会结束的日期,即.那么以实数为端点的区间可以表示为( )A、 B、 C、 D、
-
11、已知 , 下列不等式中一定成立是( )A、 B、 C、 D、
-
12、若 , 则下列不等式正确的是( )A、 B、 C、 D、
-
13、已知 , 集合 , 则与的关系正确的是( )A、 B、 C、 D、
-
14、已知集合且 , 集合 , 则( )A、 B、 C、 D、
-
15、已知平行六面体如图所示, , .
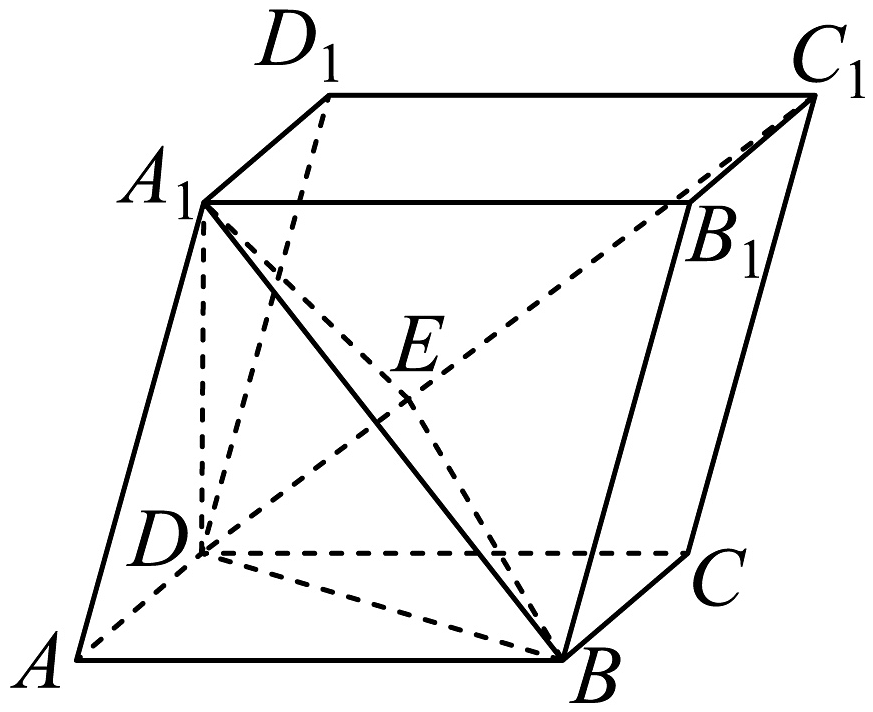 (1)、求证:平面;(2)、若 , 求二面角的余弦值.
(1)、求证:平面;(2)、若 , 求二面角的余弦值. -
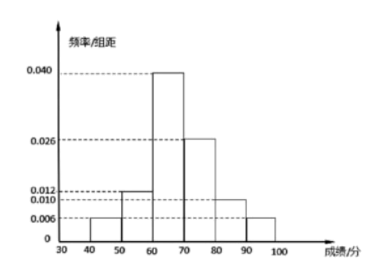
16、为迎接新一年五四青年节,某中学举办了一次名为《回首辉煌路,做好接班人》的党团史竞赛并计划对成绩前10%的学生进行颁奖.试卷满分为100分,所有学生成绩均在区间分内.已知该校高一、高二、高三年级参加的学生人数分别为200、250、300.现用分层抽样的方法抽取了75名学生的答题成绩,绘制了如下样本频率分布直方图.
年级
样本平均数
样本方差
高一
75
75
高二
69
高三
55
(1)、根据样本频率分布直方图估计该校全体学生成绩的众数、平均数以及得奖的最低分数;(2)、已知所抽取各年级答题成绩的平均数、方差的数据如下表,且根据频率分布直方图估计出总成绩的方差为80,求高三年级学生成绩的平均数和高二年级学生成绩的方差. -
17、已知 , , 分别为角 , , 的对边,.(1)、求;(2)、若 , , 点在边上,且是的角平分线,求.
-
18、已知函数.(1)、求的最小正周期和值域;(2)、先将的图象向左平移个单位,再保持纵坐标不变,横坐标缩小到原来的 , 得到的图象,求的单调递增区间.
-
19、已知函数在区间内不存在零点,则的取值范围是.
-
20、已知一底面边长为的正三棱柱有内切球,则该正三棱柱外接球的表面积为.