-
1、如图所示,某高中校运动会,拟在一张矩形海报纸上设计大小相等的左右两个矩形宣传栏发布预赛成绩与决赛成绩,宣传栏的面积之和为 , 为了美观,要求海报上四周空白的宽度均为 , 两个宣传栏之间的空隙的宽度为 , 设海报纸的长和宽分别为.
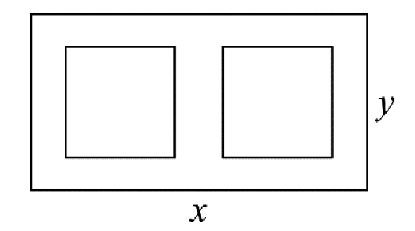 (1)、求y关于x的函数表达式;(2)、为节约成本,应如何选择海报纸的尺寸,可使用纸是最少?
(1)、求y关于x的函数表达式;(2)、为节约成本,应如何选择海报纸的尺寸,可使用纸是最少? -
2、已知函数是定义在上的偶函数,且当时,.现已画出函数在y轴左侧的图象,如图所示.
 (1)、画出在轴右侧的图象并写出函数的增区间;(2)、写出函数的解析式;(3)、讨论方程解的个数.
(1)、画出在轴右侧的图象并写出函数的增区间;(2)、写出函数的解析式;(3)、讨论方程解的个数. -
3、(1)若 , 求的最小值,并写出取得最小值时的值.
(2)若 , 求函数的最小值,并写出取得最小值时的值.
-
4、已知集合 ,(1)、分别求与;(2)、已知 , 若 , 求实数a的取值范围.
-
5、设函数 , 则.
-
6、若幂函数的图象经过点 , 则函数的定义域为.
-
7、设是一个数集,且至少含有两个数,若对任意 , 都有(除数),则称是一个数域.例如有理数集是一个数域;现有两个数域与.下列关于这两个数域的命题中是真命题的为( )A、数域中均含的元素0,1. B、有理数集. C、是一个数域 D、整数集.
-
8、集合U,S,T,F的关系如图所示,那么下列关系中正确的是( )
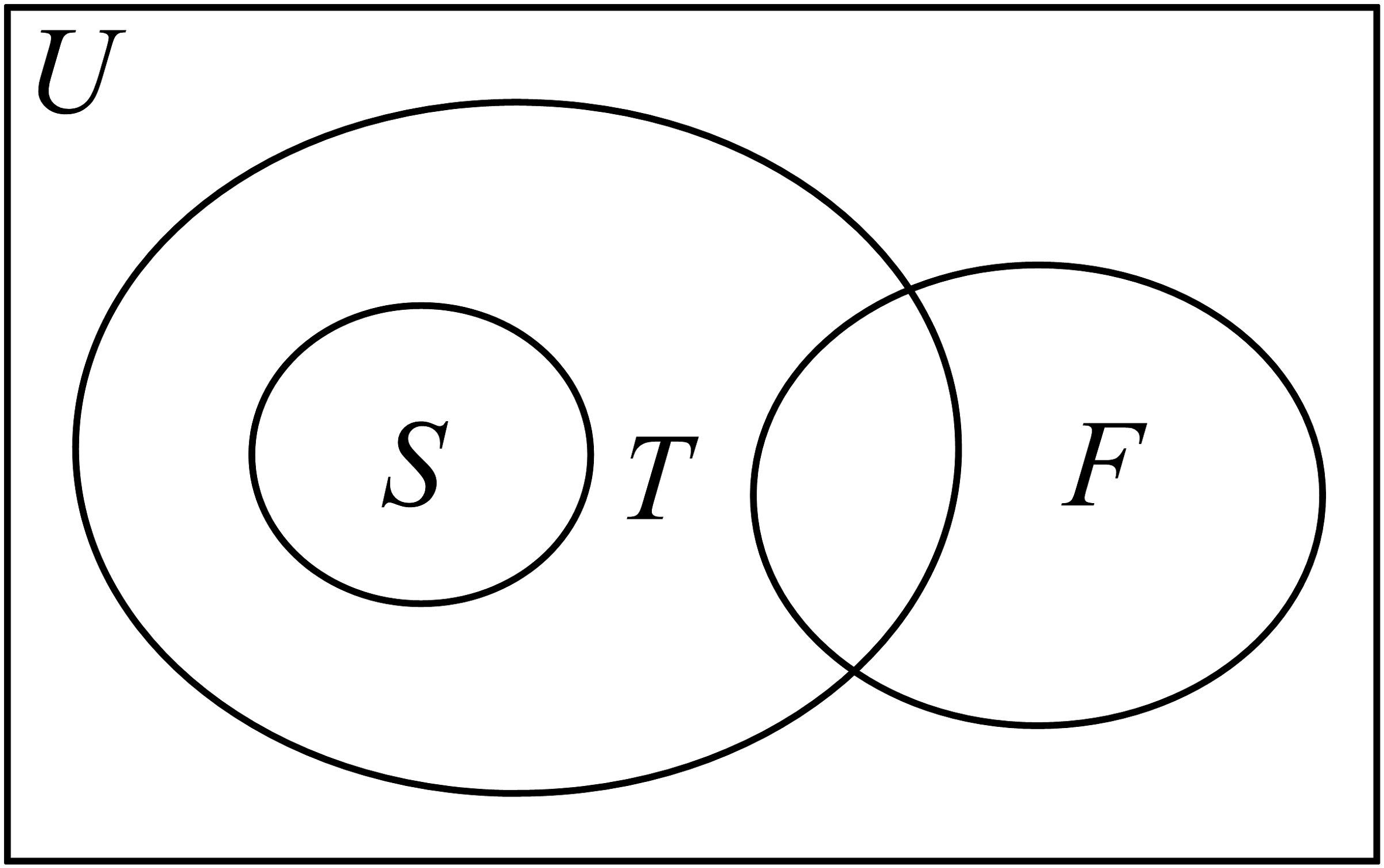 A、 B、 C、 D、
A、 B、 C、 D、 -
9、已知函数的定义域为 , 值域为 , 则( )A、函数的定义域为 B、函数的值域为 C、函数的定义域和值域都是 D、函数的定义域和值域都是
-
10、已知函数在上是减函数,则实数a的取值范围为( )A、 B、 C、 D、
-
11、已知函数 , 且最大值为( )A、0 B、 C、 D、
-
12、“”是“”成立的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
13、下列结论正确的是( )A、若 , 则 B、若 , 则 C、 D、若 , 则
-
14、已知命题 , 若p为真命题,则的取值范围是( )A、 B、 C、 D、
-
15、已知集合 , 则( )A、 B、 C、 D、
-
16、在《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马,将四个面都为直角三角形的四面体称为鳖臑.如图,已知阳马中,侧棱底面;且 , 在的中点中选择一个记为点 , 使得四面体为鳖臑.
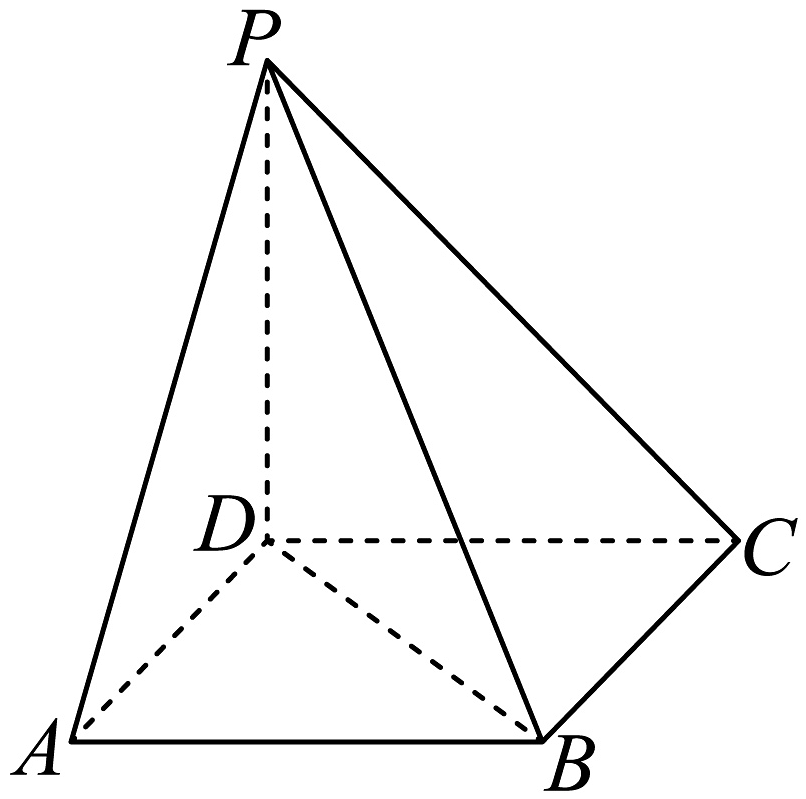 (1)、确定点的位置,并证明四面体为鳖臑;(2)、若底面是边长为1的正方形,求平面与平面夹角的余弦值.
(1)、确定点的位置,并证明四面体为鳖臑;(2)、若底面是边长为1的正方形,求平面与平面夹角的余弦值. -
17、已知圆的圆心在直线上,且过点 ,(1)、求圆的方程;(2)、若直线与圆交于、两点,求线段的长度.
-
18、如图所示,在三棱锥中, , 直线两两垂直,点分别为棱的中点.
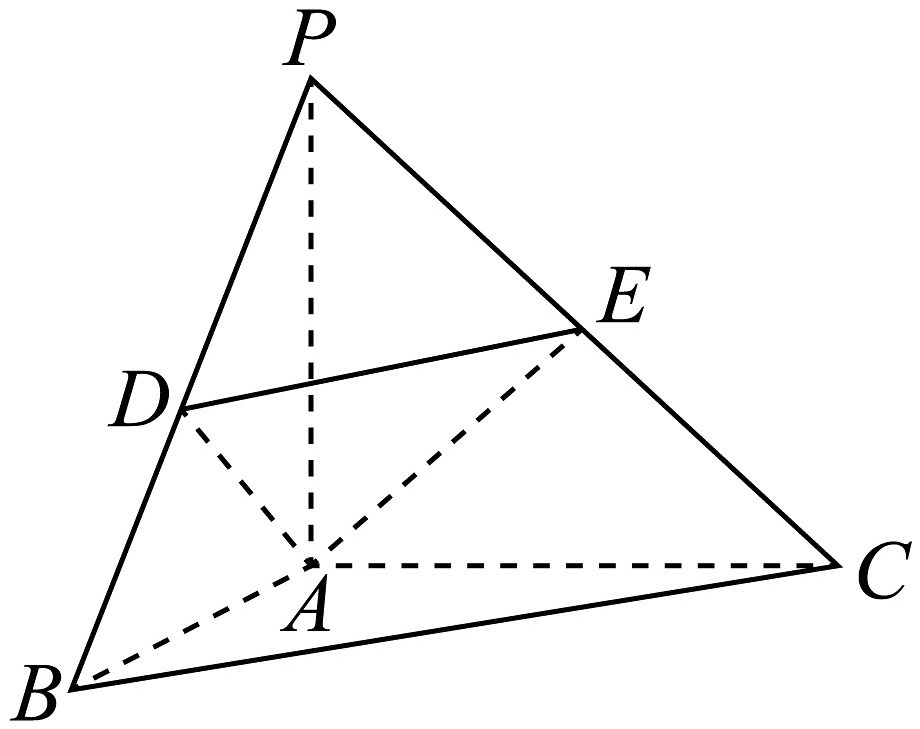 (1)、证明:平面;(2)、求平面与平面所成角的余弦值.
(1)、证明:平面;(2)、求平面与平面所成角的余弦值. -
19、直线的方程为 , .(1)、若直线在两坐标轴上的截距相等,求的方程;(2)、若直线分别交轴、轴的正半轴于点、 , 点是坐标原点.若的面积为 , 求的值.
-
20、已知点为直线上的动点,过点作圆的切线 , 切点为 , 则周长的最小值为 .