高中物理教科版-试题列表-第613页

1、在空间站中，宇航员长期处于失重状态，为缓解这种状态带来的不适，科学家设想建造一种环形空间站，如图所示。圆环旋转舱绕中心匀速旋转，宇航员站在旋转舱内的侧壁上，可以受到与他站在地球表面时相同大小的支持力，宇航员可视为质点。下列说法正确的是（　　）

A、宇航员相对自身静止释放一小球，小球将悬浮在空间站中相对空间站静止 B、旋转舱的半径大小和转动角速度乘积是定值 C、宇航员在旋转舱与旋转中心之间的连接舱中时和在地球上感受相同 D、以旋转中心为参考系，宇航员在环形旋转舱的加速度大小等于重力加速度的大小

查看解析

2、空间内存在竖直向下的匀强电场。建立如图所示x-O-y平面直角坐标系，并在第三、四象限内添加垂直于此坐标平面的某一匀强磁场（图中未画出）。现有一个质量为m、电荷量为

- q

的带负电小球，从y轴上的A点（0，L）以速度

v_{0}

抛出，经x轴上C点（2L，0）进入磁场。已知重力加速度为g。

(1)、若电场强度

E = \frac{m g}{q}

，求小球运动至C点时的速度与x轴的夹角（用三角函数表示）；

(2)、若电场强度

E = \frac{m g}{q}

，磁场垂直纸面向里，该小球能回到抛出点A，求磁感应强度B的大小；

(3)、若小球从A点以

v_{0} = \sqrt{g L}

沿x轴正方向水平抛出，磁场垂直纸面向外，且磁感应强度大小为

B = \frac{m}{2 q} \sqrt{\frac{g}{L}}

，求小球回到与A点等高（纵坐标相同）位置的x坐标。

查看解析

3、如图，半径为R光滑半圆形轨道在最低点A与左侧光滑水平面相切，可视为质点的小球P、Q之间有一被压缩的轻质弹簧（弹簧与物块不栓接），静止在水平面上。若固定小球P，释放弹簧，小球Q离开弹簧后从A进入半圆轨道，经最高点C落回水平面的位置与A距离为2R；若P不固定，释放弹簧，小球Q离开弹簧后从A进入半圆轨道，在图示B点脱离轨道。已知R、小球Q的质量m、

θ = 30 °

、重力加速度g，求：

(1)、被压缩弹簧初始时弹性势能

E_{p}

；

(2)、小球P的质量

m_{P}

。

查看解析

4、如图，一绝热长方体箱体侧壁固定一电阻为

R = 9 Ω

的电热丝，箱体总体积

V = 2 \times 1 0^{- 3} m

箱体内有一不计质量的活塞，其与箱体内壁摩擦不计。活塞左侧空间封闭一定质量的理想气体，外界大气压强

p_{0} = 1 0^{5} P a

，箱口处设有卡环。电阻丝经导线与一圆形线圈形成闭合回路，线圈放置于有界匀强磁场中，线圈平面与磁场方向垂直，磁感应强度大小随时间的变化率为

k = 0.5 T / s

。已知线圈的匝数

n = 100

，面积

S = 0.2 m^{2}

，线圈的电阻

r = 1 Ω

。初始时活塞到右侧箱口距离是到左侧箱底距离的2倍，接通电路缓慢对气体加热，加热前气体温度为

T_{0}

。

(1)、求电热丝两端的电压；

(2)、经一段时间，活塞缓慢运动到箱口，此过程中箱内气体的内能增加了100J，若电热丝产生的热量全部被气体吸收，求此时箱内气体的温度及电路的通电时间。

查看解析

5、某电学实验小组的同学发现一种旧式手机电池所标的电动势是4.45V，决定利用实验室所能提供的下列实验器材对其电动势和内电阻进行测量。

A.电流表A（量程100mA，内阻 $1 Ω$ ）

B.电压表V（量程3.0V，内阻约 $4 k Ω$ ）

C.滑动变阻器 $R_{1}$ （阻值范围0~50 $Ω$ ，额定电流1.5A）

D.电阻箱 $R_{2}$ （阻值范围0~9999 $Ω$ ）

E.电阻箱 $R_{3}$ （阻值范围0~99.99 $Ω$ ）

F.各类开关和导线若干

小组成员设计了如图所示的实验电路图。

(1)、现将该电流表与

R_{3}

并联，改装成一个量程为500mA的大量程电流表，电阻箱

R_{3}

的阻值应调为

Ω

；

(2)、为满足测量要求，需要将电压表的量程扩大为4.5V，小组成员采用如下操作：按图连好实验器材，检查无误后，开关

S_{2}

接b，将

R_{1}

的滑片滑至最左端，

R_{2}

的阻值调为0，开关

S_{3}

断开，闭合开关

S_{1}

，适当调节

R_{1}

的滑片，使电压表的示数为3.0V；保持

R_{1}

的滑片位置不变，改变电阻箱

R_{2}

的阻值，当电压表示数为V，完成扩大量程，断开开关

S_{1}

；

(3)、保持电阻箱

R_{2}

的阻值不变，将开关

S_{2}

接到a，闭合开关

S_{1}

、

S_{3}

，移动

R_{1}

的滑片，记录几组电压表V和电流表A的读数U、I，并做出图像，如图所示，可得电池的电动势

E =

V、内阻

r =

Ω

。（计算结果均保留3位有效数字）

查看解析

6、某学习小组在英国数学家兼物理学家阿特伍德《关于物体的直线运动和转动》的文章中查到了理想的阿特伍德机原理，并在实验室中进行了实验：如图所示将质量相等的两钩码A、B通过轻质细线相连绕过定滑轮，再把重物C挂在B的下端，A的下端连接纸带，已知打点计时器所用交流电源的频率为50Hz。

(1)、某次实验打出的纸带如图所示，则打出纸带上H点时钩码A的瞬时速度大小为m/s；（结果保留三位有效数字）

(2)、已知钩码的质量为M，重物C的质量为m，由静止释放。某次实验中从纸带上测量A由静止上升h高度时对应计时点的速度为v，如果满足关系式则可验证系统机械能守恒；

(3)、小组同学还改变重物C的质量m，测得多组m及其对应的加速度大小a，并在坐标纸上做出了如右图所示的

\frac{1}{a} - \frac{1}{m}

图线，根据此图线可求出当地的重力加速度大小为。

查看解析

7、某兴趣小组设计制作了一种磁悬浮列车模型，原理如图所示，PQ和MN是固定在水平地面上的两根足够长的平直导轨，导轨间分布着竖直（垂直纸面）方向等宽度的匀强磁场

B_{1}

和

B_{2}

，

B_{1}

方向未知（图中未画出），

B_{2}

垂直纸面向里。矩形金属框固定在实验车底部（车厢与金属框绝缘），其中ad边长与磁场宽度相等。当磁场

B_{1}

和

B_{2}

同时以速度

v_{0} = 10 m / s

沿导轨向右匀速运动时，金属框受到磁场力，实验车被带动沿导轨运动，能达到的最大速率为8m/s。已知金属框总电阻

R = 0.8 Ω

、垂直导轨的ab边长

L = 0.1 m

，实验车与金属框的总质量

m = 4.0 k g

，

B_{1} = B_{2} = 2.0 T

。实验车运动时受到的阻力恒定。下列说法正确的是（　　）

A、为使金属框运动，则

B_{1}

垂直纸面向外； B、实验车受到恒定阻力

f = 0.4 N

； C、在带动实验车与金属框的运动过程中，外力对磁场额外做的功等于实验车及金属框总功能的改变量与摩擦生热之和； D、若两磁场

t = 0

时刻由静止开始向右匀加速直线运动，发现

t_{1} = 2 s

时实验车开始运动，

t_{2} = 24 s

时实验车正向右做匀加速直线运动，则

t_{2}

时刻实验车的速度大小为

v = 2 m / s

。

查看解析

8、如图所示，电源电动势

E = 9 V

，内阻

r = 6 Ω

，电阻

R_{1} = 4 Ω

，

R_{2} = 8 Ω

，

R_{4} = 3 Ω

，

R_{3}

是可变电阻，电容器电容

C = 4 μ F

， a、b分别为电容器上下两个极板，G为灵敏电流表。初始时开关

S_{1}

闭合、

S_{2}

断开，电路稳定，现将开关

S_{2}

也闭合直至电路再次稳定，则下列说法正确的是（　　）

A、开关

S_{1}

闭合，

S_{2}

断开电路稳定时电容器

b

极板带正电 B、

S_{2}

闭合后，调节

R_{3}

使得上下两极板电势相等时

R_{3} = 1.5 Ω

C、若

R_{3} = 1 Ω

，则

S_{2}

闭合前后电路稳定时电源的输出功率相等 D、若

R_{3} = 1 Ω

，则在整个过程中流过电流表的电荷量为

1.7 \times 1 0^{- 5} C

查看解析

9、如图所示的变压器，输入电压为220V，可输出电压为12V、24V、36V，匝数为

n_{1}

的原线圈输入电压瞬时值表达式为

u = U_{m} s i n (100 π t)

。单匝线圈绕过铁芯连接交流电压表，电压表的示数为0.1V。将阻值为

12 Ω

的电阻R接在BC两端时，功率为12W。下列说法正确的是（　　）

A、

n_{1} = 2200

，

U_{m} = 220 \sqrt{2} V

B、BC间线圈匝数为120匝，通过R的电流为1.4A C、若将R接在AB两端，R两端的电压为24V，频率为100Hz D、若将R接在AC两端，通过R的电流为3.0A，周期为0.02s

查看解析

10、从空中某点分别以速度

v_{01}

、

v_{02}

、

v_{03}

将三个相同的小球1、2、3沿垂直于竖直墙壁方向水平抛出，三小球分别经时间

t_{1}

、

t_{2}

、

t_{3}

，下落

h_{1}

、

h_{2}

、

h_{3}

高度后与墙壁碰撞，相碰时速度大小分别为

v_{1}

、

v_{2}

、

v_{3}

，速度与竖直方向的夹角分别为60°、45°、30°，则下列结论不正确的是（　　）

A、

t_{1} : t_{2} : t_{3} = 1 : \sqrt[4]{3} : \sqrt{3}

B、

v_{01} : v_{02} : v_{03} = \sqrt{3} : \sqrt[4]{3} : 1

C、

h_{1} : h_{2} : h_{3} = 1 : \sqrt{3} : 3

D、

v_{1} : v_{2} : v_{3} = 2 : \sqrt{3} : 2

查看解析

11、一根质量为m的重绳，悬挂在两根不等高的竖直杆上。左端悬点处切线与杆夹角为

α

，右端悬点处切线与杆夹角为

β

，重力加速度为g，则重绳最低点（弧底）的张力大小为（　　）

A、

m g \frac{s i n (α + β)}{s i n α s i n β}

B、

m g \frac{s i n α s i n β}{s i n (α + β)}

C、

m g \frac{c o s α c o s β}{s i n (α + β)}

D、

m g \frac{c o s (α + β)}{c o s α c o s β}

查看解析

12、法国科学家皮埃尔·德·费马在1662年提出光线传播的路径是所需时间最少的路径，即费马原理，光的折射即遵从这一原理实际生活中的下述现象也可类比折射定律来理解。如图所示，地面上陶陶在距笔直的河岸10m处的A点，发现落水的琪琪位于水面上距河岸50m处的B点。陶陶在地面上奔跑的速度大小为

v_{1} = 5 m / s

，在水中游泳的速度大小为

v_{2}

，奔跑、游泳均视为匀速直线运动。可知此次营救中，陶陶在陆地的速度与河岸夹角30°，在水中的速度与河岸夹角60°将最省时。由题中信息和所学物理知识可知（　　）

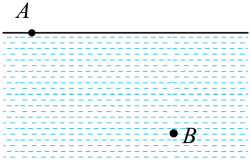A、陶陶在水中游泳的速度大小为

v_{2} = \frac{5 \sqrt{3}}{3} m / s

B、陶陶在水中游泳的速度大小为

v_{2} = 2.5 m / s

C、陶陶到达琪琪处的最短时间为12s D、陶陶到达琪琪处的最短时间约为16s

查看解析

13、甲乙两列简谐横波在同一介质中传播，

t = 0

时刻的部分波形如图，沿x轴正向传播的甲波如实线所示，沿x轴负向传播的乙波如虚线所示，波速均为4cm/s。则下列说法正确的是（　　）

A、乙波的周期为4.8s B、甲波的振幅为

A = 40 c m

C、

t = 0

时刻，介质中偏离平衡位置位移为40cm的相邻质点间的距离为24cm D、两列波可以形成稳定的干涉

查看解析

14、 2025年开年之际，国际上唯一的我国超导托卡马克大科学装置集群正在加快推动聚变能源的开发和应用，其中一种核聚变反应方程式为

_{1}^{2} H +_{1}^{3} H \to_{2}^{4} H e +_{0}^{1} n

，已知各元素原子核及中子的质量如下表，阿伏加德罗常数

N_{A}

取

6.0 \times 1 0^{23} m o l^{- 1}

，氘核摩尔质量为

2 g \cdot m o l^{- 1}

， 1u相当于931.5MeV。则下列说法正确的是（　　）

元素原子核或中子	氘核 $(_{1}^{2} H)$	氚核 $(_{1}^{3} H)$	氦核 $(_{2}^{3} H e)$	中子 $(_{0}^{1} n)$
质量（单位：u）	2.0141	3.0161	4.0026	1.0087

A、该核反应过程释放能量，不满足能量守恒定律 B、氘核的比结合能比氦核的大 C、氘核与氚核间距达到

1 0^{- 10} m

量级即可发生核聚变反应 D、4g氘完全参与聚变释放出能量的量级为

1 0^{25} M e V

查看解析

15、波是传递能量的一种方式。某一简谐波的振幅为A、圆频率为

ω

（

ω

在波传播过程中保持不变），用

\bar{ε}

表示波在传播过程中的平均能量密度，即单位体积内具有的能量，则有

\bar{ε} = \frac{1}{2} ρ A^{2} ω^{2}

，（

ρ

为介质的密度）；用I表示波在传播过程中的能流密度，即单位时间内流过垂直传播方向的单位面积上的平均能量。若不计传播过程中的能量损耗，该简谐波沿直线传播的速度为v，则有（　　）

A、

I = \frac{ρ A^{2} ω^{2} v}{2}

B、

I = ρ A^{2} ω^{2} v

C、

I = \frac{ρ A^{2} ω^{2}}{2 v}

D、

I = \frac{ρ A^{2} ω^{2}}{v}

查看解析

16、歼-35A是由中国航空工业集团自主研制的新一代中型隐身多用途战斗机。如图所示歼-35A战机先水平向右，再沿曲线ab向上，最后沿陡斜线直入云霄。设飞行路径在同一竖直面内，飞行速率不变。则在沿ab段曲线飞行过程中（　　）

A、战机水平方向的分速度逐渐增大 B、战机在某点加速度方向可能沿轨迹的切线方向 C、战机克服重力做功的功率逐渐增大 D、战机所受合外力斜向左上方且保持不变

查看解析

17、如图，置于圆形水平转台边缘的小物块随转台缓慢加速转动，当转速达到某一数值时，物块恰好滑离转台开始做平抛运动。现测得转台半径

R = 1.0 m

，离水平地面的高度

H = 1.25 m

，物块平抛落地过程水平位移的大小

s = 1.0 m

。设物块所受的最大静摩擦力等于滑动摩擦力，取重力加速度

g = 10 {m/s}^{2}

求：

(1)、物块做平抛运动的初速度大小

v_{0}

；

(2)、物块离开转台边缘时转台的角速度

ω_{0}

；

(3)、物块与转台间的动摩擦因数

μ

。

查看解析

18、如图所示为质量

m = 200 kg

的月球探测器，在执行探测任务时悬停的高度

h_{1} = 35 m

。探测器完成任务后关闭发动机自由下落，当速度达到

v = 8 m/s

时立即启动发动机提供升力，探测器向下匀减速运动，当速度减小到零时，探测器离月球表面的高度

h_{2} = 5 m

，此时再次关闭发动机，探测器最终安全达到月球表面。已知月球表面的重力加速度g取

1.6 {m/s}^{2}

。

(1)求探测器到达月球表面时速度的大小；

(2)求探测器减速过程中发动机提供升力的大小；

(3)求探测器整个下落过程所用的总时间。

查看解析

19、某班的一些同学在学习了平抛运动和圆周运动的有关知识后，自发组建了一个物理兴趣小组，想自己动手做实验来研究平抛运动的规律以及探究向心力大小的表达式。实验时，这些同学分成了三个小组，其中第一小组的同学利用如图甲所示的实验装置“研究平抛运动”，通过描点画出平抛小球的运动轨迹。

(1)、关于该实验，以下说法正确的有（　　）

A、小球运动的轨道可以不光滑，但斜槽轨道末端必须保持水平 B、每次小球可以从不同位置释放 C、实验中最好选用密度大，体积小的小球 D、为了得到小球的运动轨迹，需要用平滑的曲线把所有的点都连起来

(2)、第二小组的同学让小球做平抛运动用频闪照相机对准方格背景照相，拍摄到如图乙所示的照片，已知每个小方格边长10cm，当地的重力加速度g取10m/s² ，其中第4个点处位置已被污迹覆盖。若以拍摄的第1个点为坐标原点，水平向右和竖直向下为正方向建立直角坐标系，则被拍摄到的小球在第4个点位置的坐标为（cm）。小球平抛的初速度大小为m/s。

(3)、第三小组的同学利用如图丙所示的装置探究向心力大小的表达式，长槽上的挡板B到转轴的距离是挡板A的2倍，长槽上的挡板A和短槽上的挡板C到各自转轴的距离相等转动手柄使长槽和短槽分别随变速塔轮匀速转动，槽内的球就做匀速圆周运动。