-
1、在平直公路上，甲车以初速度从地先匀加速后匀减速运动到地，到地时速度也为 ， 乙车以初速度从地先匀减速后匀加速运动到地，到地时速度也为 ， 设两次匀加速与匀减速运动过程加速度大小均相同，关于两车的运动过程，以下说法正确的是（ ）A、两车的运动时间相同 B、甲车的运动时间较长 C、两车的平均速度相同 D、甲车的平均速度较大
-
2、一质点做直线运动的位移s与时间t的关系为（位移单位为m、时间单位为s），则该质点（ ）A、第1s内的位移是7m B、任意1s内的速度变化量都是 C、任意相邻1s内的位移之差都是1m D、质点的初速度为
-
3、如图所示，滑雪运动员不借助雪杖，由静止从山坡匀加速滑过 ， 又匀减速在平面上滑过后停下，测得 ， 设运动员在山坡上滑行的加速度大小为 ， 在平面上滑行的加速度大小为 ， 则为（ ）
A、 B、 C、 D、 -
4、甲、乙两物体同时从同一位置沿同一直线运动，甲的位移—时间图像和乙的速度—时间图像如图所示，则从原点出发后（ ）
A、0～6s甲做往返运动，乙做单向直线运动 B、乙物体在0～2s和4～6s加速度相同 C、2～4s甲乙两物体的位移均为零 D、0～6s甲的平均速率为 ， 乙的平均速率为 -
5、如图所示的是一火箭竖直上升的图像，下列几条叙述中，不符合图像所示的是（ ）
A、在40s末火箭已达到上升的最大速度 B、火箭达到最高点的时刻是120s末 C、在40s之前，火箭的加速度为 D、在40s之后，火箭的加速度为 -
6、东京奥运会后，全红婵马不停蹄地代表广东参加在陕西举行的全运会。10米跳台比赛中，全红婵跳台自由下落，经时间t入水，全程可视为初速度为0的匀加速直线运动。全红婵下落后第一个时间内的位移为 ， 最后一个时间内的位移为 ， 则（ ）A、 B、 C、 D、
-
7、仔细观察如图所示的时间轴，下列说法正确的是（ ）
A、第3s初是指时间轴上的D点 B、第3s内是指时间轴上AD段 C、前4s内是指时间轴上AE段 D、第2s内是指时间轴上的C点 -
8、下列各物理量中，全部都是矢量的选项是（ ）A、位移、速度、速率、加速度 B、位移、速度、平均速度、加速度 C、路程、速率、时间、质量 D、位移、时间、平均速率、加速度
-
9、甲、乙两同学计划从A地到B地，手机导航软件推荐了两条路线，如图所示，他们分别沿路线1和2到达B地，但用时不同。从A地到B地，他们一定具有相同的（ ）
A、位移 B、路程 C、平均速度 D、加速度 -
10、如图所示，一人跳伞后飞机上的飞行员（甲）和地面上的人（乙）观察跳伞者的运动后，引发了对跳伞人员运动状况的争论，下列说法正确的是（ ）
A、甲、乙两人的说法中必有一个是错误的 B、他们的争论是由于参考系的选择不同而引起的 C、研究物体运动时不一定要选择参考系 D、参考系的选择只能是相对于地面静止的物体 -
11、某人在一公交车后方距观后镜的距离处，突然公交车由静止开始以的加速度做匀加速直线运动，经后人以某一速度匀速追赶公交车（忽略人的加速过程），司机通过观后镜能看到后方的最远距离 ， 并且人要在观后镜中至少出现4 s司机才能发现。
（1）若人以的速度匀速追赶，求人距观后镜的最小距离有；
（2）求人要能被司机发现，人匀速追赶公交车的最小速度。
-
12、如图所示，一滑块从固定斜面顶端A由静止下滑，最终停在C点。已知AD的高度h=3m，BD的长度L1=4m，AD⊥BD，斜面与水平面在B点平滑连接，BC的长度L2=10m，小滑块从A点运动至C点的总时间为5s，假定小滑块在AB上做匀加速直线运动，在BC上做匀减速直线运动，求：
(1)、小滑块滑至B点时的速度大小vB；(2)、小滑块从A运动到C点的平均速度的大小（可用根式表示）；(3)、若在C点正上方H=20m处有一小球，某时刻将小球由静止释放，不计空气阻力，取g=10m/s2 ， 小球恰好与刚刚停下的滑块在C点相遇，求释放小球瞬间滑块离B点的距离。 -
13、运动员把冰壶沿水平冰面推出，让冰壶在冰面上自由滑行，在不与其他冰壶碰撞的情况下，最终停在远处的某个位置。按比赛规则，投掷冰壶运动员的队友，可用毛刷在冰壶滑行前方来回摩擦冰面，减小冰面的动摩擦因数以调节冰壶的运动。现将冰壶以v0=4m/s的速度投掷出去，发现其滑行总距离为x=40m，假设冰壶在冰面上自由滑行时做匀减速直线运动，求：
(1)、冰壶自由滑行7.6m后的速度大小v1；(2)、在冰壶自由滑行7.6m后，运动员开始在冰壶滑行前方摩擦冰面，冰壶运动的加速度变为原来的0.9倍，求：（i）冰壶全程运动的总时间t；
（ii）比原来多运动的距离。
-
14、已知一物体在一水平面上向右做匀加速直线运动，加速度大小为a=2m/s2 ， 求：(1)、若初速度为v0=2m/s，求物体在t=2s时的速度，(2)、若初速度为v0=2m/s，求物体在t=2s时的位移大小；(3)、若初速度为零，求物体在x=2m处与x=4m处的速度大小之比。
-
15、某学习小组要完成实验“探究小车速度随时间变化的关系”。(1)、打点计时器是最基本的（填“计时”或“测速”）仪器，A组同学采用了如图所示的打点计时器，则他们的纸带位置放置正确的是（填“A”或“B”），该打点计时器应接在学生电源的两孔上（填“AC”或“DC”）；
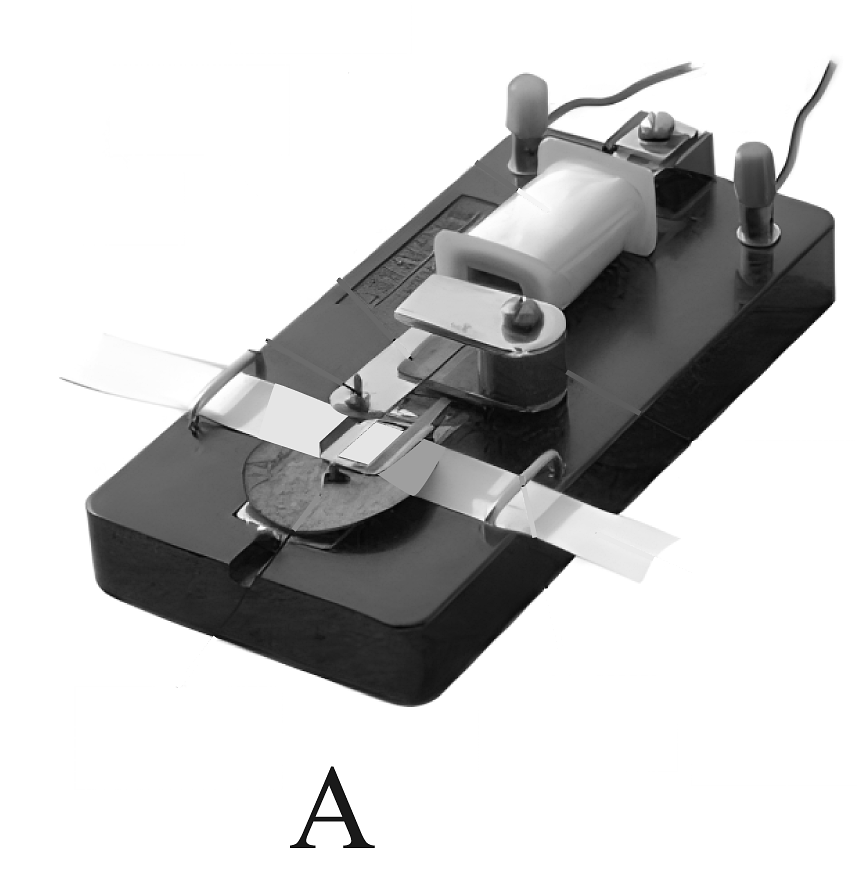
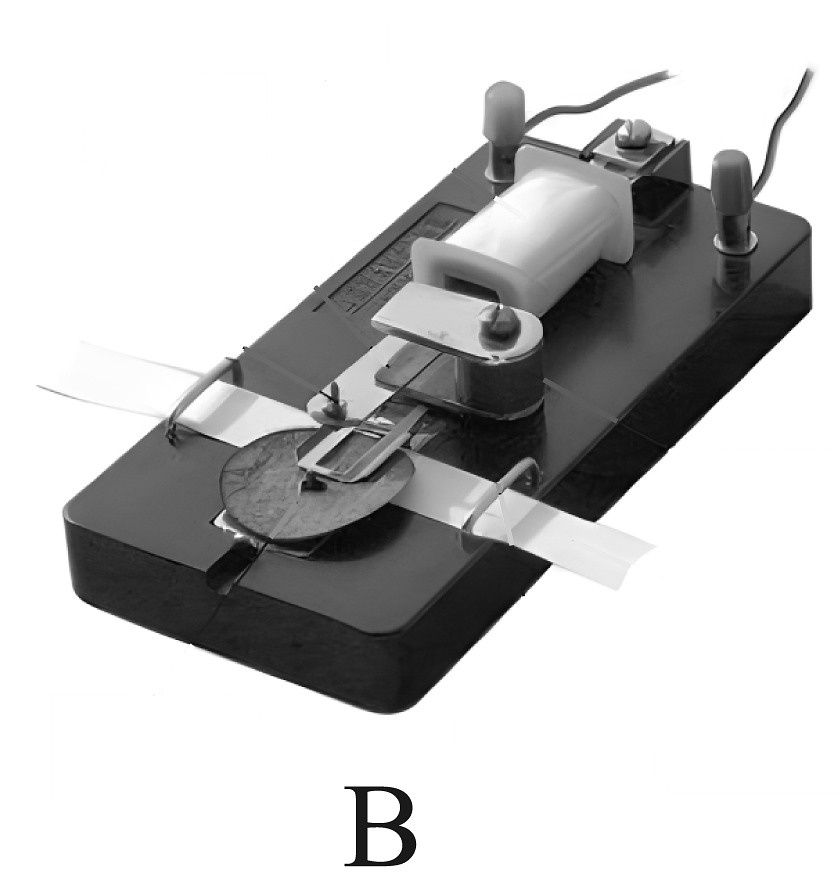
(2)、在本实验中，必须要保证的操作是（ ）A、先打开打点计时器，再释放小车 B、细线必须与桌面平行 C、小车应从靠近打点计时器处释放 D、长木板带滑轮的一侧必须要垫高(3)、如图是经打点计时器打出的纸带的一段，打点顺序是A、B、C、D、E，已知交流电源的频率为50Hz，纸带上每相邻两个计数点间还有四个点未画出。现把一刻度尺放在纸带上，其零刻度线和计数点A对齐，则B点的刻度尺读数为cm，打下计数点时纸带的瞬时速度vC=m/s（保留两位有效数字），根据记录的数据，得到小车运动的加速度大小是m/s2（保留两位有效数字）；
(4)、得到结果后A组同学发现，他们所用的刻度尺并不标准，刻度尺上的1mm实际上有1.1mm长，则由此得到的加速度的大小相比于真实值（填“偏大”、“偏小”、“不变”），该误差属于（填“系统误差”或“偶然误差”）；(5)、B组同学是采用作v-t图像的方式求解加速度，较合理的方法是（ ）A、根据任意两计数点的速度，用公式求解加速度 B、根据数据作出v-t图，量出其倾角θ，由公式a=tanθ求出加速度 C、根据数据作出v-t图，取图像上较远两点，用公式求解加速度 D、依次算出两点间的加速度，取平均值后作为小车的加速度(6)、C组同学为了证明小车作匀变速直线运动，采用了以下方法：先把纸带每隔0.1s剪断，得到若干短纸条，再把这些纸条并排贴在一张纸上，使这些纸条下端对齐，最后将纸条上端中心连起来，得到如图所示图像，这样的方法（填“可行”、“不可行”）。
-
16、从某一高度先后由静止释放两个相同的小球甲和乙，若两球被释放的时间间隔为1s，在不计空气阻力的情况下，它们在空中的运动过程中（ ）A、在空中运动时，甲、乙两球的距离越来越大 B、在空中运动时，甲、乙两球的速度之差越来越大 C、甲、乙两球落地的时间差受初始释放的高度影响，初始高度越高，落地时间差越小 D、若某次甲球以20m/s落地，经0.1s后以10m/s反弹，则此过程中甲球的平均加速度大小为300m/s2
-
17、下列运动可能存在的是（ ）A、物体加速度逐渐减小，但速度逐渐增大 B、物体速度为零，但加速度却很大 C、物体向上运动，而加速度却向下 D、物体速度变化量方向为正，速度方向也为正，但物体做减速运动
-
18、某物体做单向匀变速直线运动，则其相邻相等时间间隔的两段位移之比可能为（ ）A、2：7 B、4：7 C、9：2 D、4：1
-
19、某航空母舰以速度v0（未知）匀速航行，为保证飞机能安全起飞，战斗机起飞时的速度须达v=50m/s。假设飞机原本和航母保持相对静止，飞机匀加速的最大加速度是a=5.0m/s2 ， 该航空母舰甲板长L=160m，为了使飞机能安全起飞，航空母舰的速度v0至少为（ ）A、10m/s B、20m/s C、30m/s D、40m/s
-
20、一辆公交车在平直的公路上从A站出发运动至B站停止，经历了匀加速、匀速、匀减速三个过程，设加速和减速过程的加速度大小分别为a1、a2 ， 匀速过程的速度大小为v，则（ ）A、增大a1 ， 保持a2、v不变，整个过程的平均速度可能变小 B、减小a1 ， 保持a2、v不变，匀速运动过程的时间一定变短 C、增大v，保持a1、a2不变，全程时间一定变长 D、只要v不变，不论a1、a2如何变化，全程平均速度不变