版本：

全部人教版（2019）粤教版（2019）教科版（2019）鲁科版（2019）沪科版（2019）人教版沪科版鲁科版粤教版苏教版教科版

相关试卷

1、2023年诺贝尔物理学奖授予三位物理学家以表彰他们发现了一种产生极短（阿秒as）光脉冲的方法。这种光脉冲可用于测量电子移动或能量变化的快速过程，为人类探索原子和分子的内部提供了新工具。阿秒是时间单位， $1 as = 10^{- 18} s$ 。下列不是国际单位制的基本单位的是（　　）

A、牛顿 B、千克 C、安培 D、米

查看解析
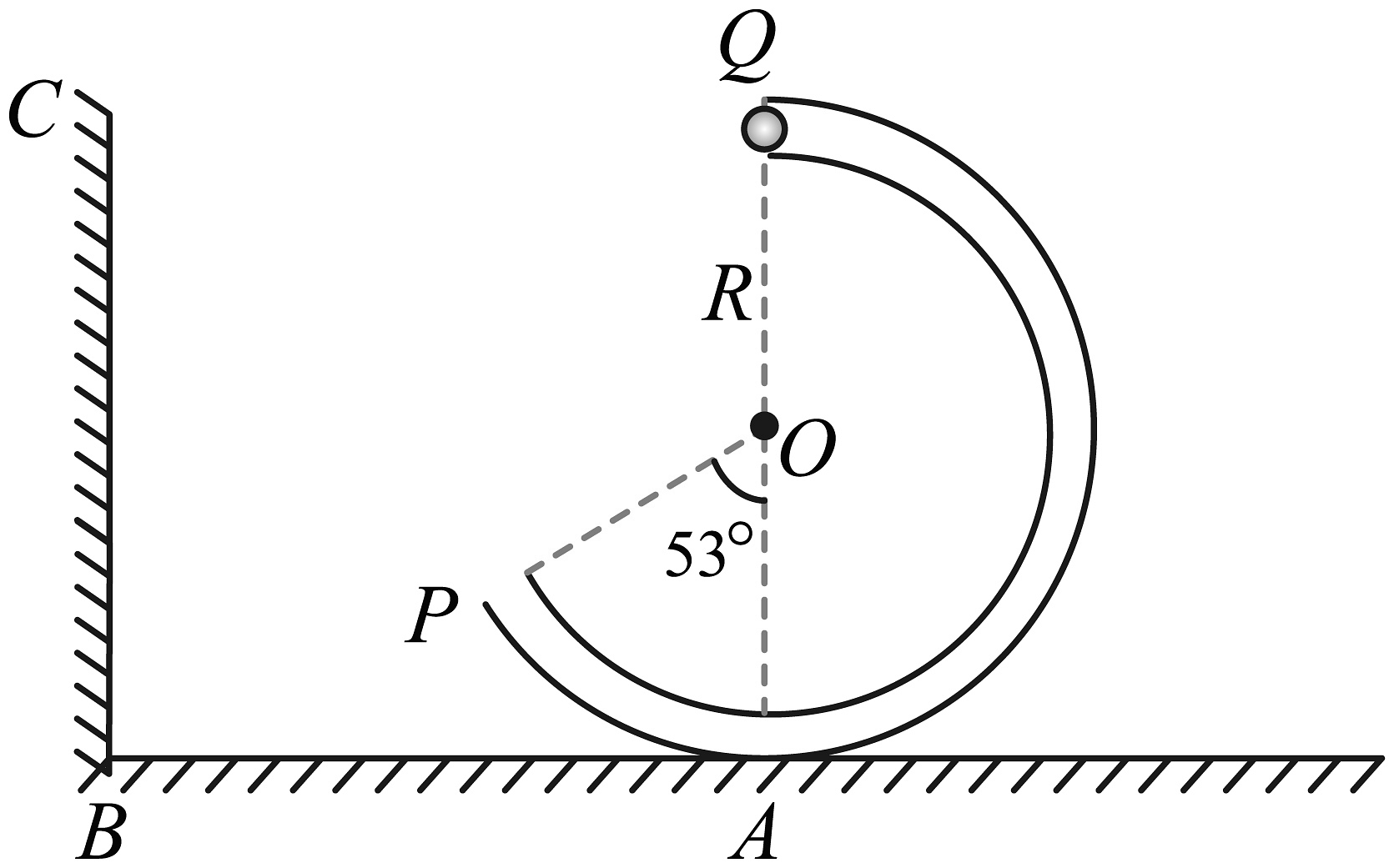
2、如图所示，竖直平面内光滑细管弯成的圆弧形轨道半径 $R = 0.5 m$ ，质量 $m = 1 kg$ 的小球在最高点Q受到轻微扰动，由静止沿管道从右侧滑下。小球经最低点A从管道 $P$ 点飞出后恰好垂直打在竖直墙面BC上的E点（图中未画出），OP与OA的夹角 $θ = 53^{\circ}$ 。已知小球直径远小于 $R$ 且可视为质点，重力加速度 $g$ 取 $10 m / s^{2}$ ， $sin 53^{\circ} = 0.8$ ， $cos 53^{\circ} = 0.6$ 。求：
（1）小球到达 $P$ 点时，管道对小球弹力的大小和方向；
（2）Q、E之间的高度差 $h$ 。

查看解析
3、“氢气型”电动汽车利用氢气和氧气直接反应生成水，对环境没有污染。其发动机的额定功率为24 kW，汽车连同驾乘人员总质量为m=2 t，在水平路面上行驶时受到的阻力是800 N，汽车在额定功率下匀速行驶，求：
（1）匀速行驶的速度大小。
（2）阻力做功的功率大小。

查看解析
4、用自由落体法验证机械能守恒定律，装置如图甲所示。

(1)、关于该实验，下列说法正确的是______。

A、应选用质量大、密度小的重锤 B、需要用天平测量重物的质量 C、应先释放纸带再接通电源 D、实验时，应调节计时器使它的限位孔与纸带处在同一竖直线上

(2)、打点计时器所接交流电源的频率为50Hz，选取一条点迹清晰的纸带（如图乙所示），打点计时器所打的第一点为O点，舍去前面间隔较短的点迹（图中未画出），在适当位置选取打点计时器连续打下的3个点A、B、C。测得 $O A = 25.90 cm$ ， $O B = 30.55 cm$ ， $O C = 35.50 cm$ ，已知重锤的质量为200g，当地重力加速度 $g = 9.8 {m/s}^{2}$ 。打点计时器打下B点时重锤的速度 $v_{B} =$ m/s。（计算结果保留两位有效数字）

(3)、重物从O点运动到B点，重力势能减少量 $Δ E_{p} =$ J，动能的增加量 $Δ E_{k} =$ J。（计算结果保留两位小数）

(4)、对比 $Δ E_{p}$ 和 $Δ E_{k}$ 的数值，你可以得出的结论是。

查看解析
5、2018年12月27日，中国北斗三号基本系统完成建设，开始提供全球服务。北斗三号卫星导航系统空间段由5颗静止轨道卫星和30颗非静止轨道卫星组成。假如静止轨道卫星先沿椭圆轨道1飞行，后在远地点P处点火加速，由椭圆轨道1变成静止圆轨道2，下列说法正确的是（）

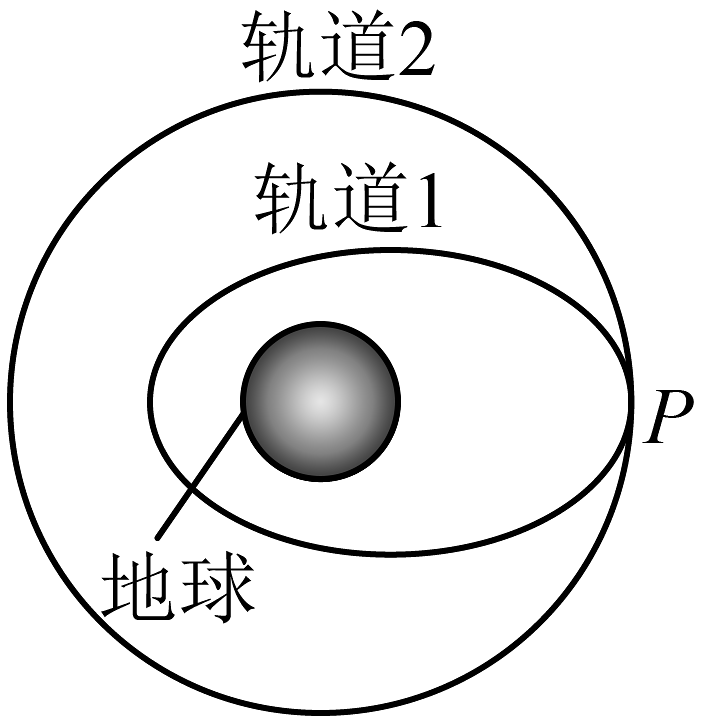A、卫星在轨道2上运行时的速度小于7.9km/s B、卫星变轨前后的速度相等 C、卫星在轨道2上运行时的向心加速度比在赤道上相对地球静止的物体的向心加速度小 D、卫星在轨道1上的P点和在轨道2上的P点的加速度大小相等

查看解析
6、如图所示，小球以5m/s的速度水平抛开，经过0.8s落地，取g=10m/s² ，不计空气阻力，下列说法正确的有( )

A、小球在水平方向的位移大小是3.2m B、小球在竖直方向的位移大小是3.2m C、小球落地时在水平方向的速度大小是5m/s D、小球落地时在竖直方向的速度大小是5m/s

查看解析
7、某质点做曲线运动的轨迹如图中虚线所示，则下列各图中标出的质点通过位置P时的速度v、加速度a的方向，可能正确的是

A、 B、 C、 D、

查看解析
8、某同学设计了一个电容式风力传感器，如图所示，将电容器与静电计组成回路，可动电极在风力作用下向右移动，风力越大，移动距离越大（两电极始终不接触）。在风力变大时（　　）

A、电容器电容变大，静电计指针张角变大 B、电容器电容变大，静电计指针张角变小 C、电容器电容变小，静电计指针张角变大 D、电容器电容变小，静电计指针张角变小

查看解析
9、“高台滑雪”一直受到一些极限运动爱好者的青睐。挑战者以某一速度从某曲面飞出，在空中表演各种花式动作，飞跃障碍物（壕沟）后，成功在对面安全着陆。某同学利用物块演示分析该模型的运动过程：如图所示，ABC为一段光滑圆弧轨道，B为圆弧轨道的最低点。P为一倾角θ＝37°的固定斜面，斜面顶端表面处铺有一木板DE，木板上边缘与斜面顶端D重合，圆轨道末端C与斜面顶端D之间的水平距离为x＝0.32m。一物块以某一速度从A端进入圆形轨道ABC后从C端沿圆弧切线方向飞出，再经t＝0.2s恰好平行于木板从D端滑上木板，且恰好没有从木板滑离，斜面足够长。已知物块m＝1kg，木板质量M＝1kg，木板与物块之间的动摩擦因数从 $μ_{1} = \frac{7}{8}$ ，木板与斜面之间的动摩擦因数从 $μ_{2} = \frac{3}{4}$ ，重力加速度 $g = 10 m / s^{2}$ ， sin37°＝0.6，不计空气阻力，求：
（1）物块从C端飞出时的速度 $v_{C}$ 的大小，和 $v_{C}$ 与水平方向夹角的余弦值；
（2）木板的长度L；
（3）若将木板分成等长的两部分，其间平滑接触且不粘连，求最终小物块的速度。

查看解析
10、从在某星球表面一倾角为 $θ$ 的山坡上以初速度v₀平抛一物体，经时间t该物体落到山坡上．已知该星球的半径为R，一切阻力不计，引力常量为G，求：
（1）该星球表面的重力加速度的大小g
（2）该星球的质量M．

查看解析
11、在“探究加速度与物体受力、物体质量的关系”实验中，某实验小组利用如图所示的实验装置，将一端带滑轮的长木板固定在水平桌面上，木块置于长木板上，并用细绳跨过定滑轮与砂桶相连，小车左端连一条纸带，通过打点计时器记录其运动情况。

(1)、在本实验中，保持力不变，探究加速度与质量的关系，这种研究方法叫做___________。

A、控制变量法 B、等效替代法 C、理想化方法

(2)、下列做法正确的是________（多选）

A、调节滑轮的高度，使牵引木块的细绳与长木板保持平行 B、在探究加速度与力的关系时，作a--F图象应该用折线将所描的点依次连接 C、实验时，先放开木块再接通打点计时器的电源 D、通过增减小车上的砝码改变质量时，不需要重新调节木板倾斜度

(3)、下图是实验时平衡阻力的情形，其中正确的是________（选填字母）

A、 B、 C、.

(4)、某学生在平衡摩擦力时，把长木板的一端垫得过高，使得倾角偏大。他所得到的a–F关系可用图中的________表示（图中a是小车的加速度，F是细线作用于小车的拉力）。

A、 B、 C、 D、

(5)、如图是打出纸带的一段，相邻计数点间还有四个点未画出，已知打点计时器使用的交流电频率50 Hz。由图可知，打纸带上B点时小车的瞬时速度v_B=m/s，木块的加速度a=m/s²。（结果保留两位有效数字）

查看解析
12、如图所示，某航天器围绕一颗半径为R的行星做匀速圆周运动，其环绕周期为T，经过轨道上A点时发出了一束激光，与行星表面相切于B点，若测得激光束AB与轨道半径AO夹角为θ，引力常量为G，不考虑行星的自转，下列说法正确的是（　　）

A、行星的质量为 $\frac{4 π^{2} R^{3}}{G T^{2} \sin^{3} θ}$ B、行星的平均密度为 $\frac{3 π}{G T^{2} \sin^{3} θ}$ C、行星表面的重力加速度为 $\frac{4 π^{2} R}{T^{2} \sin^{3} θ}$ D、行星的第一宇宙速度为 $\frac{2 π R}{T \sin θ}$

查看解析
13、拨浪鼓是一种小型的儿童玩具，其简化的模型如上图所示。拨浪鼓边缘上与圆心等高处关于手柄对称的左右两侧位置固定有长度分别为l₁和l₂的两根不可伸长的轻质细绳，两细绳的另一端分别系有质量相同的小球甲、乙。保持手柄竖直匀速转动，使得两球均在水平面内匀速转动，连接甲、乙的细绳与竖直方向的夹角分别为α和β，若α<β，则（　　）

A、甲球运动的周期大于乙球运动的周期 B、甲球运动的角速度大小等于乙球的角速度大小 C、甲球所受绳子的拉力大小小于乙球所受绳子的拉力大小 D、甲球的向心加速度大小大于乙球的向心加速度大小

查看解析
14、在儿童游乐场有一种射击游戏，地面上圆形轨道的半径为R，轨道上的小车以角速度ω做匀速圆周运动，坐在小车上的游客使用玩具枪向处于轨道圆心处的立柱射击，某次射击时子弹恰好水平击中立柱的最高点，射击时枪口到立柱最高点的水平距离为x，竖直距离为h，重力加速度为g，不计空气阻力，下列说法正确的是（　　）

A、子弹射出枪口时的速度大小为 $\sqrt{\frac{x^{2} g}{2 h} + 2 g h}$ B、子弹射出枪口时的速度大小为 $\sqrt{ω^{2} R^{2} + \frac{x^{2} g}{2 h} + 2 g h}$ C、射击时枪管与水平面的夹角为θ， $\tan θ = \frac{2 h}{x}$ D、射击时枪管与水平面的夹角为θ， $\tan θ = \frac{\sqrt{2 g h}}{\sqrt{ω^{2} x^{2} + \frac{g x^{2}}{2 h}}}$

查看解析
15、游乐场内旋转飞椅的运动可以简化为如图所示的匀速圆周运动，下列关于飞椅的受力分析正确的是（　　）

A、飞椅受到重力、悬绳拉力和向心力的作用 B、飞椅只受向心力作用 C、飞椅在运动中合外力不变 D、飞椅所受的重力和悬绳拉力的合力提供其做圆周运动的向心力

查看解析
16、内表面为半球型且光滑的碗固定在水平桌面上，球半径为R，球心为O，现让可视为质点的小球在碗内的某一水平面上做匀速圆周运动，小球与球心O的连线与竖直线的夹角为θ，重力加速度为g，则（　　）

A、小球的加速度为a = gsinθ B、碗内壁对小球的支持力为 $N = \frac{m g}{\sin θ}$ C、小球的运动周期为 $T = 2 π \sqrt{\frac{R cos θ}{g}}$ D、小球运动的速度为 $v = \sqrt{g R \tan θ}$

查看解析
17、如图所示，轻绳MN的两端固定在水平天花板上，物体m₁系在轻绳MN的某处，悬挂有物体m₂的光滑轻滑轮跨在轻绳MN上。系统静止时的几何关系如图。则m₁与m₂的质量之比为（　　）

A、1：1 B、1：2 C、1： $\sqrt{3}$ D、 $\sqrt{3}$ ：2

查看解析
18、如图所示，在 $x$ 轴下方空间内存在竖直方向的匀强电场，在第Ⅳ象限内同时还存在垂直坐标平面向里，磁感应强度大小为 $B$ 的匀强磁场。将一群带负电的微粒从第Ⅱ象限内的不同位置以初速度 $v_{0}$ 沿 $x$ 轴正方向抛出，发现这些带电微粒均能经过坐标原点 $O$ 。带电微粒通过 $O$ 点后进入第Ⅳ象限内做匀速圆周运动，经过磁场偏转后都能再次到达 $y$ 轴。已知带电微粒电量为 $q$ ，质量为 $m$ ，重力加速度为 $g$ 。求：

(1)、这群带电微粒从第Ⅱ象限内射出的位置坐标满足的方程；

(2)、第Ⅳ象限内匀强磁场区域的最小面积；

(3)、若在第Ⅲ象限所在的立体空间内充满沿 $y$ 轴正方向的匀强磁场（图中未画出），磁感应强度大小也为 $B$ ，求带电微粒在这个区域运动时到 $y$ 轴的最远距离。

查看解析
19、如图所示，光滑水平面AB与竖直面内的光滑半圆形导轨在B点平滑相接，导轨半径为 $R$ 。一质量为 $M$ 的木块放在水平面AB上，质量为 $m$ 的子弹以水平速度 $v_{0}$ 射入木块，子弹留在木块中。若木块能沿半圆形导轨滑到最高点C，重力加速度为 $g$ ，求：

(1)、子弹射入木块过程中产生的热量 $Q$ ；

(2)、若 $m = M$ ，且木块从C点飞出后落地点与B点的距离 $s = 4 R$ ，求子弹击中木块前的水平速度 ${v^{'}}_{0}$ 的大小。

查看解析
20、如图所示，导热性能良好的圆筒形汽缸开口向右放置在水平地面上，质量为 $m = 2 kg$ 、横截面积 $S = 10 {cm}^{2}$ 的活塞在汽缸内封闭了一定质量的理想气体，开始的封闭气柱的长度为 $L = 18 cm$ ，环境温度为27℃，大气压强 $p_{0} = 1.0 \times 10^{5} Pa$ 。现将汽缸逆时针旋转 $90 °$ 使其开口端竖直向上，取 $g = 10 {m/s}^{2}$ ，不计活塞厚度，汽缸内壁光足够长且不漏气，取0℃为 $273 K$ 。

(1)、求活塞稳定后封闭气柱的长度；

(2)、活塞稳定后再将环境温度缓慢升高至 $T = 400 K$ ，若升温过程中气体吸收 $25J$ 的热量，求该过程中气体的内能变化量。

查看解析

上一页 1119 1120 1121 1122 1123 下一页跳转