相关试卷
- 上海市松江区2017年高考物理二模试卷
- 上海市松江区2017年高考物理一模试卷
- 上海市浦东新区四校联考2016-2017学年高二上学期物理期中考试试卷
- 上海师大附中2016-2017学年高一上学期物理期中考试试卷
- 陕西省延安市黄陵中学重点班2016-2017高二下学期物理期末考试试卷
- 河南省开封市兰考二高2016-2017高二下学期物理期末考试试卷
- 陕西省延安市黄陵中学高新部2016-2017学年高一下学期物理期末考试试卷
- 陕西省安康市石泉中学2016-2017学年高一下学期物理期末考试试卷
- 河南省开封市开封县祥符中学2016-2017学年高一下学期物理期末考试试卷
- 陕西省延安市黄陵中学2016-2017学年高三上学期物理期末考试试卷
-
1、实验课上同学们做了两组实验,请帮助完成以下内容:(1)、利用电火花计时器等器材,研究小车做匀加速直线运动的规律,其中一个小组的同学从所打的几条纸带中选取了一条点迹清晰的纸带,如图所示,图中O、A、B、C、D是按打点先后顺序依次选取的计数点,两相邻计数点之间还有四个打出点没有画出,电源频率为50Hz。

由图中的数据可知,打下C点时的速度大小为=m/s;小车运动的加速度大小a=(以上计算结果均保留两位有效数字)。
(2)、在“探究两个互成角度的力的合成规律”实验中,提供以下器材:薄木板一块,量程为5N的弹簧测力计两个、橡皮条(带有两个较长的细绳套)、白纸、刻度尺以及图钉若干个。①关于实验及操作建议,正确的有
A.同一次实验过程中O点位置可以变动
B.用两个测力计拉橡皮条时必须互成90°
C.读数时视线应正对测力计刻度
D.拉橡皮条时,测力计、橡皮条、细绳必须与木板平面平行
②某次测量时测力计的示数如图所示,则其读数为N;

③某同学用同一套器材做了四次实验,白纸上留下的标注信息有结点位置O、力的标度、分力和合力的大小及表示力方向的点,如下图所示。其中最能提高实验精度且符合实验事实的是
A.
 B.
B.
C.
 D.
D.
-
2、甲乙两车在平直公路上的两相邻车道行驶,乙车在前,甲车在后。两车的图像如图所示,下列判断正确的是( )
 A、乙车刹车的加速度大小是甲车的2倍 B、两车第一次平齐的时刻可能发生在12s末 C、若时刻两车沿运动方向距离为12m,两车平齐的时刻只有一次 D、若时两车平齐,则时两车沿运动方向距离为18.25m
A、乙车刹车的加速度大小是甲车的2倍 B、两车第一次平齐的时刻可能发生在12s末 C、若时刻两车沿运动方向距离为12m,两车平齐的时刻只有一次 D、若时两车平齐,则时两车沿运动方向距离为18.25m -
3、一平面内有三个大小相等的共点力,如图甲、乙、丙、丁所示,各图的合力大小分别记为、、、 , 则下列判断正确的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
4、如图,质量为m的物块在平行于斜面的拉力F作用下沿倾角为θ的斜面做匀速直线运动。物块与斜面间的动摩擦因数μ = tanθ,重力加速度为g,则拉力F的大小不可能为( )
 A、mgsinθ B、 C、2mgsinθ D、
A、mgsinθ B、 C、2mgsinθ D、 -
5、如图所示,一质量为m=8kg的木块放在水平桌面上,在水平方向受到F1和F2作用而处于静止状态,其中F1=10N,F2=3N。已知木块与地面的动摩擦因数为0.1,最大静摩擦力等于滑动摩擦力。重力加速度大小取 , 则木块在水平方向受到的摩擦力Ff下列说法正确的是( )
 A、若撤去F1保留F2 , 则Ff=8N,方向向左 B、若撤去F1保留F2 , 则Ff=3N,方向向右 C、若撤去F2保留F1 , 则Ff=3N,方向向左 D、若撤去F2保留F1 , 则Ff=10N,方向向左
A、若撤去F1保留F2 , 则Ff=8N,方向向左 B、若撤去F1保留F2 , 则Ff=3N,方向向右 C、若撤去F2保留F1 , 则Ff=3N,方向向左 D、若撤去F2保留F1 , 则Ff=10N,方向向左 -
6、已知甲乙两物体做直线运动,甲的图像和乙的图像如图所示,以下说法正确的是( )
 A、甲在时速度为零 B、乙在前6s内的路程为6m C、前3s内甲的位移与乙的位移大小相等 D、前6s内甲乙都做的是匀变速直线运动
A、甲在时速度为零 B、乙在前6s内的路程为6m C、前3s内甲的位移与乙的位移大小相等 D、前6s内甲乙都做的是匀变速直线运动 -
7、有下列几种情景,请根据所学知识选择对情景的分析和判断正确的说法( )
①沿直线高速行驶的汽车为避免事故发生紧急刹车
②点火后即将升空的火箭
③火车由静止加速到40km/h需要20秒;汽车由静止加速到100km/h需要15秒
④运动的磁悬浮列车在轨道上高速行驶
A、①汽车紧急刹车时,速度变化率大,所以加速度大 B、②因火箭还没运动,所以加速度一定为零 C、③火车的加速度大于汽车的加速度 D、④高速行驶的磁悬浮列车,因速度很大,所以加速度很大 -
8、以下物理量是标量的是( )A、位移 B、平均速率 C、速度 D、加速度
-
9、某些肿瘤可以用“质子疗法”进行治疗。如图所示,来自质子源的质子初速度为零,经加速电压U(U未知)加速后,沿图中四分之一圆弧虚线通过辐向电场,再从P点竖直向上进入存在水平向右的匀强电场的圆形区域,最终轰击处在圆上Q点的肿瘤细胞。已知四分之一圆弧虚线处的场强大小为 , 方向均沿半径指向圆心O,圆与OP相切于P点, , 圆形电场区域的半径为R,Q点位于OP上方处,S点位于OP上方R处,质子质量为m、电量为e。不计质子间相互作用。求:
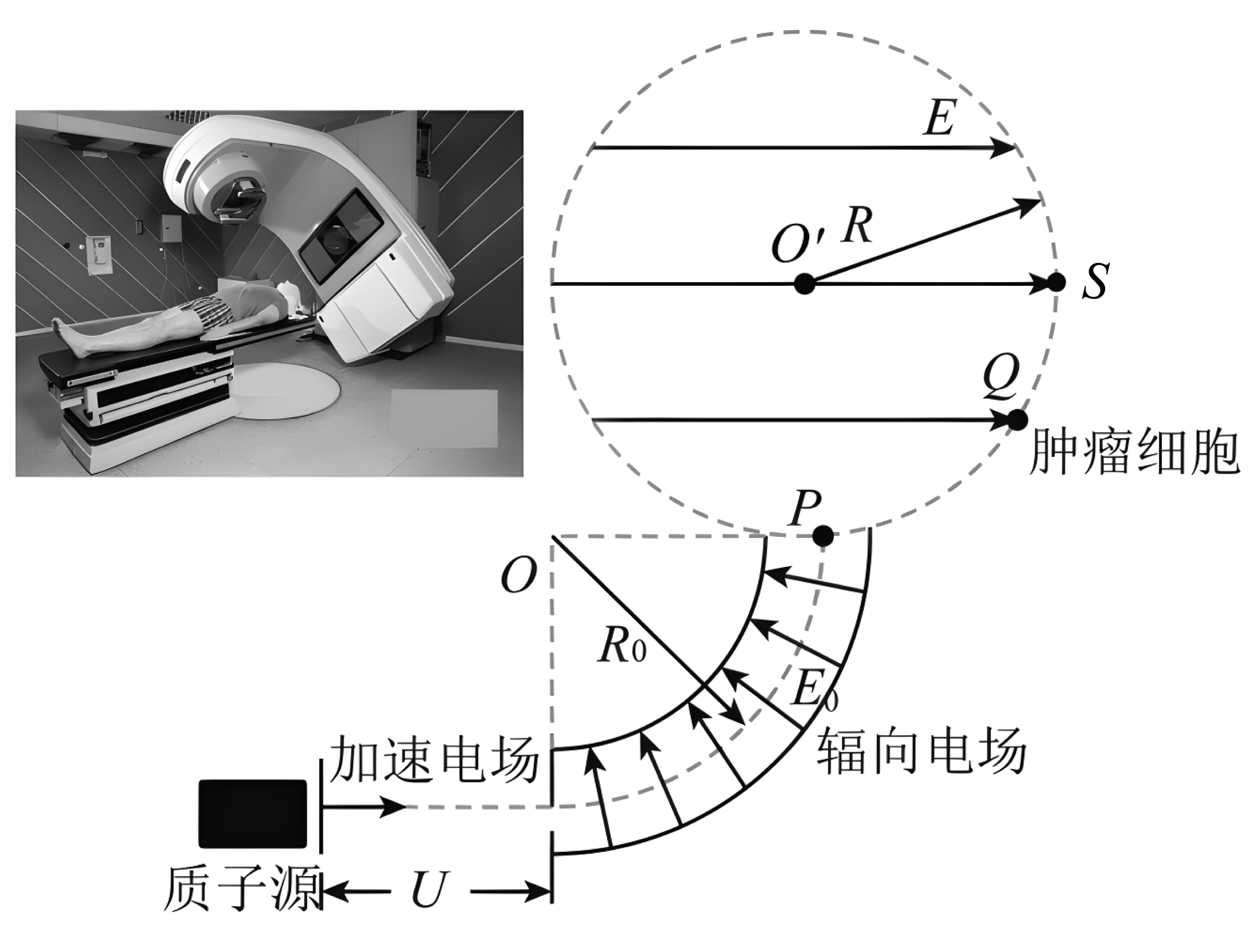 (1)、质子在辐向电场做匀速圆周运动的速度大小v,加速电场的电压U。(2)、质子轰击到Q点的肿瘤细胞时对应匀强电场的场强大小E;(3)、若将加速电压改为原来倍,其它条件不变,试通过计算分析质子能否击中位于圆上S处肿瘤细胞。
(1)、质子在辐向电场做匀速圆周运动的速度大小v,加速电场的电压U。(2)、质子轰击到Q点的肿瘤细胞时对应匀强电场的场强大小E;(3)、若将加速电压改为原来倍,其它条件不变,试通过计算分析质子能否击中位于圆上S处肿瘤细胞。 -
10、如图所示,在绝缘水平面上的O点固定一电荷量为+Q点电荷,在O点正上方高为H的A处由静止释放某带电荷量为+q的小液珠,开始运动的瞬间小液珠的加速度大小恰好等于重力加速度,方向竖直向上。已知静电力常量为k,两电荷均可看成点电荷,不计空气阻力。求:
(1)液珠开始运动瞬间所受库仑力的大小和方向;
(2)运动过程中小液珠速度最大时其离O点的距离h。(以上两问结果只能用题中已知的物理量k,Q,q,H表示)

-
11、简谐横波沿x轴传播,M、N是x轴上两质点,如图甲是质点N的振动图像。图乙中实线是t=3s时刻的波形图像。质点M位于x=8m处,虚线是再过Δt时间后的波形图像。图中两波峰间距离Δx=7.0m。求:
 (1)、波长λ和周期T;(2)、波速大小v和波传播方向;(3)、时间Δt。
(1)、波长λ和周期T;(2)、波速大小v和波传播方向;(3)、时间Δt。 -
12、现有一合金制成的圆柱体,为测量该合金的电阻率,现用伏安法测圆柱体两端之间的电阻,用螺旋测微器测量该圆柱体的直径,用游标卡尺测量该圆柱体的长度。螺旋测微器和游标卡尺的示数分别如图甲、乙所示。
 (1)、由上图读得圆柱体的直径为mm,长度为cm。(2)、若流经圆柱体的电流为I,圆柱体两端之间的电压为U,圆柱体的直径和长度分别为D、L,则用D、L、I、U表示的电阻率的关系式为ρ=。
(1)、由上图读得圆柱体的直径为mm,长度为cm。(2)、若流经圆柱体的电流为I,圆柱体两端之间的电压为U,圆柱体的直径和长度分别为D、L,则用D、L、I、U表示的电阻率的关系式为ρ=。 -
13、在研究单摆运动的实验中:
 (1)、图(a)是用力传感器对单摆震动过程进行测量的装置图,图(b)是与力传感器连接的计算机屏幕所显示的图像,根据图(b)的信息可得,从t=0时刻开始,摆球第一次摆到最低点的时刻为s,摆长为m(取重力加速度大小)。(2)、单摆振动的回复力是______。A、摆球所受的重力 B、摆球重力在垂直摆线方向上的分力 C、摆线对摆球的拉力 D、摆球所受重力和摆线对摆球拉力的合力(3)、某同学的操作步骤如下,其中正确的是______。A、取一根细线,下端系住直径为d的金属小球,上端固定在铁架台上 B、用米尺量得细线长度L,测得摆长为L C、在摆线偏离竖直方向小于5°位置静止释放小球 D、让小球在水平面内做圆周运动,测得摆动周期,再根据公式计算重力加速度
(1)、图(a)是用力传感器对单摆震动过程进行测量的装置图,图(b)是与力传感器连接的计算机屏幕所显示的图像,根据图(b)的信息可得,从t=0时刻开始,摆球第一次摆到最低点的时刻为s,摆长为m(取重力加速度大小)。(2)、单摆振动的回复力是______。A、摆球所受的重力 B、摆球重力在垂直摆线方向上的分力 C、摆线对摆球的拉力 D、摆球所受重力和摆线对摆球拉力的合力(3)、某同学的操作步骤如下,其中正确的是______。A、取一根细线,下端系住直径为d的金属小球,上端固定在铁架台上 B、用米尺量得细线长度L,测得摆长为L C、在摆线偏离竖直方向小于5°位置静止释放小球 D、让小球在水平面内做圆周运动,测得摆动周期,再根据公式计算重力加速度 -
14、一学习小组通过力传感器对单摆振动过程进行探究:图(a)是用力传感器对单摆振动过程进行测量的装置图,图(b)是与力传感器连接的计算机屏幕所显示的F-t图像,根据图(b)的信息可得,从t=0时刻开始摆球第一次摆到最低点的时刻为 , 摆长为(取 , 重力加速度大小g=10m/s2)。

-
15、如图所示,氕核、氘核、氚核三种粒子从同一位置无初速度地飘入电场线水平向右的加速电场,之后进入电场线竖直向下的匀强电场发生偏转,最后打在荧光屏上。整个装置处于真空中,不计粒子重力及其相互作用,下列说法正确的是( )
 A、经过加速电场的过程中,电场力对氚核做的功最多 B、经过偏转电场的过程中,电场力对三种原子核做的功一样多 C、三种原子核打在屏上的动能一样大 D、三种原子核都打在屏的同一位置上
A、经过加速电场的过程中,电场力对氚核做的功最多 B、经过偏转电场的过程中,电场力对三种原子核做的功一样多 C、三种原子核打在屏上的动能一样大 D、三种原子核都打在屏的同一位置上 -
16、熔喷布具有的独特的超细纤维结构,增加了单位面积纤维的数量和表面积,具备很好的过滤性、屏蔽性、绝热性和吸油性,使其成为医用口罩的最核心的材料。工厂在生产熔喷布时为了实时监控其厚度,通常要在生产流水线上设置如图所示的传感器,其中A、B为平行板电容器的上、下两个极板,其位置均固定,且分别接在恒压直流电源的两极上,G是灵敏电流计。当熔喷布的厚度变厚导致介电常数变大时( )
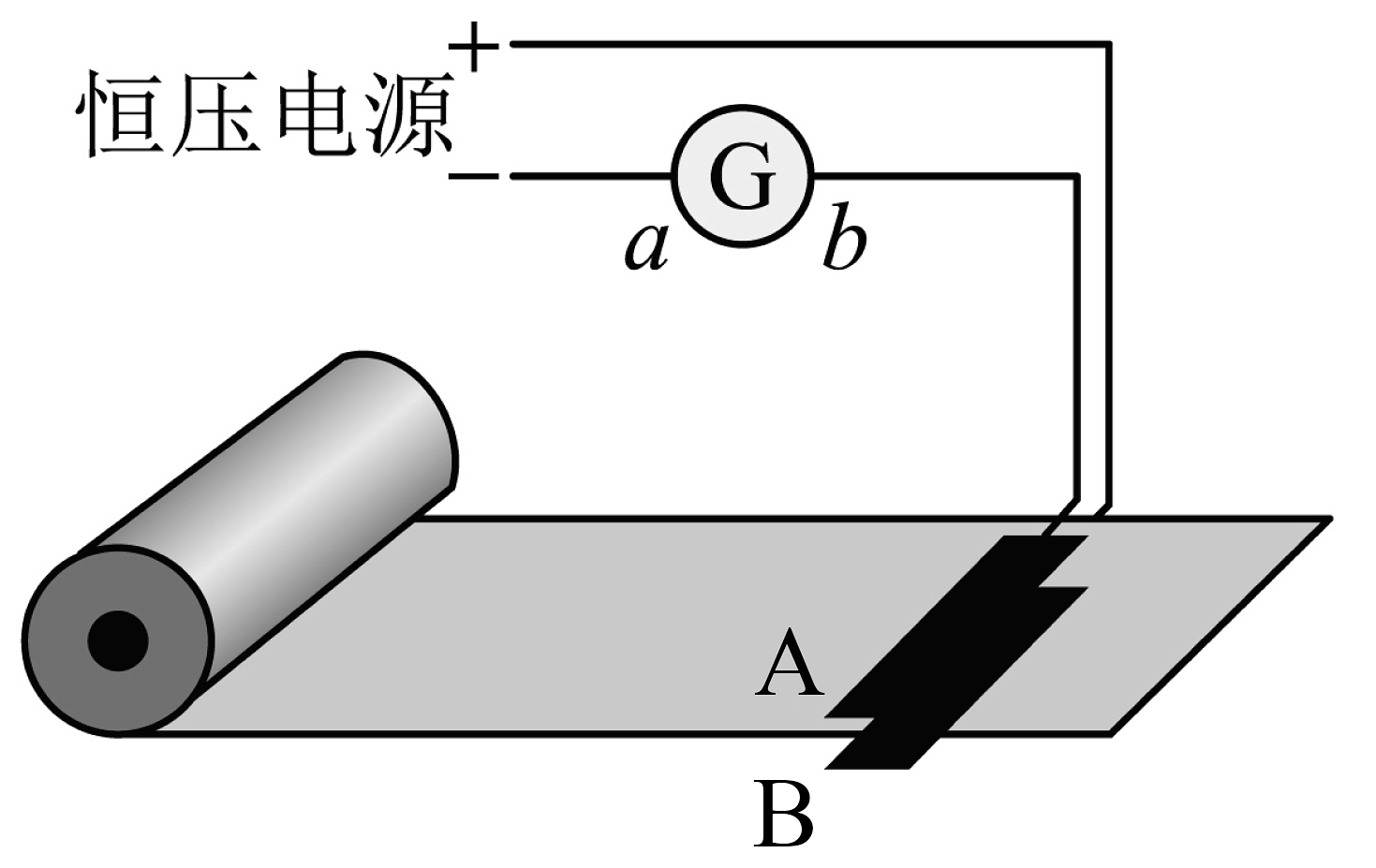 A、极板间的电场强度不变 B、极板上所带的电荷量减少 C、平行板电容器的电容变小 D、有自b向a的电流流过灵敏电流计
A、极板间的电场强度不变 B、极板上所带的电荷量减少 C、平行板电容器的电容变小 D、有自b向a的电流流过灵敏电流计 -
17、生活在尼罗河的反天刀鱼,它的器官能在其周围产生电场,电场线分布如图所示,M、N、P为电场中的点。下列说法正确的是( )
 A、P点电场强度大于M点电场强度 B、P点电势高于N点电势 C、M点电势高于N点电势 D、某带电小颗粒只在电场力作用下从N点沿虚线轨迹运动到M点,其在N点电势能大于在M点电势能
A、P点电场强度大于M点电场强度 B、P点电势高于N点电势 C、M点电势高于N点电势 D、某带电小颗粒只在电场力作用下从N点沿虚线轨迹运动到M点,其在N点电势能大于在M点电势能 -
18、如图所示,边长为2cm的正三角形ABC处于匀强电场中,电场方向平行于三角形所在平面。将电子由A点移动到B点,电场力做功6eV;将电子由A点移动到C点,电场力做功3eV。电场强度大小为( )
 A、200V/m B、300V/m C、 D、400V/m
A、200V/m B、300V/m C、 D、400V/m -
19、现有同一单色光以相同的入射角θ,打在不同浓度NaCl的两杯溶液中,折射光线如图所示 , 已知折射率随浓度增大而变大。则( )
 A、乙图溶液的折射率大 B、乙图溶液的浓度小 C、此单色光在乙图溶液中的传播速度小 D、增大入射角θ,在溶液表面均会发生全反射
A、乙图溶液的折射率大 B、乙图溶液的浓度小 C、此单色光在乙图溶液中的传播速度小 D、增大入射角θ,在溶液表面均会发生全反射 -
20、某科考小组在专业潜水员的指导下,到新丰江水库进行水下科考活动。如图所示,水中的某个组员看到水面以上的所有景物都处在一个倒立的圆锥内,已知该圆锥轴截面的顶角为a,光在真空中的传播速度为c。则光在水中的传播速度为( )
 A、 B、 C、 D、
A、 B、 C、 D、